1.2: Порядок операцій

Порядок, в якому ми оцінюємо вирази, може бути неоднозначним. Візьмемо, наприклад, вираз$-4+2 \cdot 8$. Якщо спочатку виконати додавання, то отримаємо в$-16$ результаті (знак питання над знаком рівності говорить про те, що результат сумнівний).

$$\begin{align*} -4+2 \cdot 8 &\overset{?}{=} -2 \cdot 8\\ &\overset{?}{=}-16 \end{align*} \nonumber$$

З іншого боку, якщо ми спочатку виконаємо множення, то отримаємо в$12$ результаті.

$$\begin{align*} -4+2 \cdot 8 &\overset{?}{=} -4 + 16\\ &\overset{?}{=}12 \end{align*} \nonumber$$

Отже, що нам робити? Звичайно, угруповання символів усуне неоднозначність.

Угруповання символів

Для групування частин виразу можна використовувати дужки, дужки та стовпчики абсолютних значень. Наприклад:

$$3+5(9-11) \quad \text{or} \quad-2-[-2-5(1-3)] \quad \text{or} \quad 6-3|-3-4| \nonumber$$

У кожному випадку правило полягає в тому, що «спочатку оцініть вираз всередині символів групування». Якщо символи групування вкладені, спочатку оцініть вираз у внутрішній парі символів групування.

Таким чином, якщо наведений вище приклад згрупований наступним чином, ми змушені спочатку оцінити вираз всередині дужок.

$$\begin{aligned} (-4+2) \cdot 8 &=-2 \cdot 8 \color{Red}\text { Parentheses first: }-4+2=-2 \\ &=-16 \quad \color{Red} \text { Multiply: }-2 \cdot 8=-16 \end{aligned} \nonumber$$

Ще один спосіб уникнути неясностей при оцінці виразів - встановити порядок, в якому повинні виконуватися операції. Наступні рекомендації завжди повинні суворо виконуватися при оцінці виразів.

Правила, що керують порядком операцій

При оцінці виразів дійте в наступному порядку.

1. Спочатку оцініть вирази, що містяться в групувальних символах. Якщо символи групування вкладені, спочатку оцініть вираз у внутрішній парі символів групування.
2. Оцінити всі експоненти, які з'являються у виразі.
3. Виконуйте всі множення і ділення в тому порядку, щоб вони відображалися у виразі, рухаючись зліва направо.
4. Виконуйте всі додавання і віднімання в тому порядку, щоб вони відображалися у виразі, рухаючись зліва направо.

Приклад$\PageIndex{1}$

Спростити:$-3-4 \cdot 8$.

Рішення

Через встановлені Правила, що керують порядком операцій, цей вираз вже не є неоднозначним. Тут немає угруповання символів або експонентів, тому ми відразу переходимо до правила три, оцінюємо всі множення і ділення в тому порядку, в якому вони з'являються, рухаючись зліва направо. Після цього викликаємо правило четверте, виконуючи всі додавання і віднімання в тому порядку, в якому вони з'являються, рухаючись зліва направо.

$$\begin{aligned} -3-4 \cdot 8&= -3-32 \quad \color{Red} \text { Multiply first: } 4 \cdot 8=32 \\ &= -3+(-32) \quad \color{Red} \text { Add the opposite. } \\ &= -35 \quad \color{Red} \text { Add: }-3+(-32)=-35\\ \text{Thus, } -3-4 \cdot 8&= -35 \end{aligned} \nonumber$$

Вправа$\PageIndex{1}$

Спростити:$-4+2 \cdot 8$.

Відповідь

$12$

Написання математики

При спрощенні виразів дотримуйтесь наступного правила, щоб акуратно оформити свою роботу:
Один знак рівності в рядку.

Це означає, що не варто розташовувати свою роботу горизонтально.

$$-2-4 \cdot(-8)=-2-(-32)=-2+32=30 \nonumber$$

Це три рівних знака на одному рядку. Швидше, розташуйте свою роботу вертикально, зберігаючи рівні знаки, вирівняні в стовпці.

$$\begin{aligned}-2-4 \cdot(-8) &=-2-(-32) \\ &=-2+32 \\ &=30 \end{aligned} \nonumber$$

Приклад$\PageIndex{2}$

Спростити:$54/(-9)(2)$.

Рішення

Тут немає угруповання символів або експонентів, тому ми відразу переходимо до правила три, оцінюємо всі множення і ділення в тому порядку, в якому вони з'являються, рухаючись зліва направо.

$$\begin{aligned} 54 /(-9)(2) &=-6(2) \quad \color{Red}\text { Divide first: } 54 /(-9)=-6 \\ &=-12 \quad \color{Red}\text { Multiply: }-6(2)=-12 \\ \text{Thus, } 54 /(-9)(2)&= -12 \end{aligned} \nonumber$$

Вправа$\PageIndex{2}$

Спростити:$-24 /(-3)(2)$.

Відповідь

$16$

Приклад $\PageIndex{2}$може стати джерелом плутанини для багатьох читачів. Зверніть увагу, що множення не має переваг перед діленням, а також ділення не віддає перевагу множенню. Множення і ділення мають однаковий рівень переваги і повинні виконуватися в тому порядку, щоб вони відбувалися, рухаючись зліва направо. Якщо ні, то буде отримана неправильна відповідь.

$\color{Red}\text {Warning!}$

Ось що станеться, якщо виконати множення в прикладі $\PageIndex{2}$перед діленням.

$$\begin{aligned} 54 /(-9)(2) &=54/(-18) \quad \color{Red}\text { Multiply: } (-9)(2)=-18 \\ &=-3 \quad \color{Red}\text { Divide: } 54/(-18)=-3 \end{aligned} \nonumber$$

$\color{Red}\text{This is incorrect!}$Множення і ділення необхідно виконувати в тому порядку, щоб вони відбувалися, рухаючись зліва направо.

Приклад$\PageIndex{3}$

Спростити:

1. $(-7)^{2}$
2. $-7^{2}$

Рішення

Нагадаємо, що для будь-якого цілого числа a, у нас є$(-1)a =-a$. Оскільки заперечення еквівалентно множенню на$-1$, Правила керівного порядку операцій вимагають, щоб ми розглядали символи групування та показники перед запереченням.

1. Через угруповання символів ми заперечуємо спочатку, а потім квадрат. Тобто, $$\begin{aligned}(-7)^{2} &=(-7)(-7) \\ &=49 \end{aligned} \nonumber$$
2. У цьому прикладі немає символів групування. Таким чином, ми повинні спочатку квадрат, а потім звести нанівець. Тобто, $$\begin{aligned}-7^{2} &=-(7 \cdot 7) \\ &=-49 \end{aligned} \nonumber$$

Таким чином$(-7)^2 = 49$, але$-7^2 = -49$. Примітка: Цей приклад$(-7)^2$ демонструє, що відрізняється від$-7^2$.

Вправа$\PageIndex{3}$

Спростити:$-15^{2}$.

Відповідь

$-225$

Давайте спробуємо приклад, який має суміш показників, множення та віднімання.

Приклад$\PageIndex{4}$

Спростити:$-3-2(-4)^{2}$.

Рішення

Правила, що керують порядком операцій, вимагають спочатку розглядати показники, потім множення, потім віднімання.

$$\begin{aligned} -3-2(-4)^{2} &=-3-2(16) \quad \color{Red} \text{ Exponent first: } (-4)^2 = 16 \\ &=-3-32 \quad \color{Red} \text{ Multiply: } 2(16)=32 \\ &=-3+(-32) \quad \color{Red} \text{Add the opposite.} \\ &=-35 \quad \color{Red} \text{ Add: } -3+(-32) = -35 \\ \text{Thus, } -3-2(-4)^{2} &= -35 \end{aligned} \nonumber$$

Вправа$\PageIndex{4}$

Спростити:$-5-4(-2)^{3}$.

Відповідь

$27$

Угруповання символів

Правила керівного порядку операцій вимагають, щоб вирази всередині символів групування (дужки, дужки або фігурні дужки) були оцінені першими.

Приклад$\PageIndex{5}$

Спростити:$-2(3-4)^{2}+5(1-2)^{3}$.

Рішення

Правила керівного порядку операцій вимагають, щоб ми спочатку оцінили вирази, що містяться всередині символів групування.

$$\begin{aligned} -2(3-4)^{2} + 5(1-2)^{3} &=-2(3+(-4))^{2}+5(1+(-2))^{3} \quad \color{Red} \text{ Add the opposites.}\\ &=-2(-1)^{2}+5(-1)^{3} \quad \color{Red} \text{ Parenthesis first: } 3+(-4)=-1 \text{ and } 1+(-2)=-1\\ \text {Evaluate the exponents next, perform the multiplications, then add.}\\ &= -2(1)+5(-1) \quad \color{Red} \text{ Exponents: } (-1)^2=1 \text{ and } (-1)^3=-1\\ &=-2(1)+5(-1) \quad \color{Red} \text{ Multiply: } -2(1)=-2 \text{ and } 5(-1)=-5 \\ &=-7 \quad \color{Red} \text{ Add } -2+(-5)=-7 \\ \text{Thus, } -2(3-4)^{2} + 5(1-2)^{3} &= -7 \end{aligned}\nonumber$$

Вправа$\PageIndex{5}$

Спростити:$-2-3(-2-3)^{3}$.

Відповідь

$373$

Абсолютні значення смуги як угруповання символів

Подібно дужкам і дужкам, ви повинні спочатку оцінити те, що знаходиться всередині них, а потім взяти абсолютне значення результату.

Приклад$\PageIndex{6}$

Спростити:$-8-|5-11|$.

Рішення

Спочатку ми повинні оцінити, що знаходиться всередині барів абсолютних значень.

$$\begin{aligned} -8-|5-11| &=-8-|5+(-11)| \quad \color{Red} \text{ Add the opposites.}\\ &=-8-|-6| \quad \color{Red} \text{ Add: } 5+(-11)=-6\\ \text {The number } -6 \text{ is } 6 \text{ units from zero on the number line. Hence, } |-6|=6 \\ &= -8-6 \quad \color{Red} \text{ Add: } |-6|=6\\ &= -8+(-6) \quad \color{Red} \text{ Add the opposite. } \\ &=-14 \quad \color{Red} \text{ Add. } -2+(-5)=-7 \\ \text{Thus, } -8-|5-11| &= -14 \end{aligned}\nonumber$$

Вправа$\PageIndex{6}$

Спростити:$-|-4-6|$.

Відповідь

$-10$

Вкладені символи групування

Коли символи групування вкладені, Правила керівного порядку операцій вказують нам спочатку оцінити найпотаємніші вирази.

Приклад$\PageIndex{7}$

Спростити:$-3-4[-3-4(-3-4)]$.

Рішення

Правила, що керують порядком операцій, вимагають, щоб ми спочатку зверталися до виразу, що міститься у найпотаємніших символах групування. Тобто ми спочатку оцінюємо вираз, що міститься в дужках.

\ [\ begin {вирівняний}
-3-4 [-3-4 (-3-4)] &=-3-4 [-3-4 (-3+ (-4))]\ quad\ color {Червоний}\ текст {Додати протилежне.} \\
&=-3-4 [-3-4 (-7)]\ quad\ color {Червоний}\ текст {Додати:} -3+ (-4) =-7\
\ text {Далі ми оцінюємо вираз, що міститься всередині дужок.}\\
&= -3-4 [-3- (-28)]\ quad\ color {Червоний}\ text {Множення:} 4 (-7) =-28\\
&= -3-4 [-3+28]\ квадратний\ колір {червоний}\ text {Додати протилежне.}\\
&= -3-4 [25]\ quad\ color {Red}\ text {Додати:} -3+28=25\
\ text {Тепер множимо, потім віднімаємо.} \\
&= -3-100\ квадратний\ колір {Червоний}\ текст {Множення:} 4\ {25\} =100\\
&= -3+ (-100)\ квадратний\ колір {Червоний}\ текст {Додати протилежне.}\\
&= -103\ квадратний\ колір {червоний}\ текст {Додати:} -3+ (-100) =-103\\
\ текст {Таким чином,} -3-4 [-3-4 (-3-4)] &= -103\ кінець {вирівняний} \ номер\]

Вправа$\PageIndex{7}$

Спростити:$-2-2[-2-2(-2-2)]$.

Відповідь

$-14$

Оцінювання алгебраїчних виразів

Змінна

Змінна - це символ (як правило, буква), який позначає невідоме значення, яке може відрізнятися.

Давайте додамо визначення алгебраїчного виразу.

Алгебраїчний вираз

Коли ми об'єднуємо числа та змінні дійсним способом, використовуючи такі операції, як додавання, віднімання, множення, ділення, зведення в ступінь, отримана комбінація математичних символів називається алгебраїчним виразом.

Таким чином,

$$2a, \quad x+5, \quad \text{and} \quad y^{2} \nonumber$$

утворені комбінацією чисел, змінних та математичних операторів, є дійсними алгебраїчними виразами.

Алгебраїчне вираз має бути добре сформованим. Наприклад, не $$2+-5x \nonumber$$ є дійсним виразом, оскільки немає терміну після знака «плюс» (некоректно писати ні$+−$ з чим між цими операторами). Аналогічно, не $$2+3(2 \nonumber$$ є добре сформованим, оскільки дужки не збалансовані.

У цьому розділі ми будемо оцінювати алгебраїчні вирази для заданих значень змінних, що містяться у виразах. Ось кілька простих порад, які допоможуть вам досягти успіху.

Поради щодо оцінки алгебраїчних виразів

1. Замініть усі входження змінних у виразі відкритими дужками. Залиште місце між дужками, щоб підставити задане значення змінної.
2. Підставляємо задані значення змінних у відкриті дужки, підготовлені на першому кроці.
3. Оцінити отриманий вираз відповідно до Правил Керівного Порядку операцій.

Приклад$\PageIndex{8}$

Оцініть вираз$x^{2}-2xy+y^{2}$ в$x=-3$ і$y=2$.

Рішення

Дотримуючись порад щодо оцінки алгебраїчних виразів, спочатку замініть усі входження змінних у виразі$x^{2}-2xy+y^{2}$ відкритими дужками. Далі підставляємо задані значення змінних ($-3$$2$for$x$ і$y$ for) у відкриті дужки.

$$\begin{aligned} x^{2}-2 x y+y^{2} &=(\;\; )^{2}-2(\;\;)( )+( )^{2} \\ &=({\color{Red}-3})^{2}-2({\color{Red}-3})({\color{Red}2})+({\color{Red}2})^{2} \end{aligned} \nonumber$$

Нарешті, дотримуйтесь Правил Керівного порядку операцій, щоб оцінити отриманий вираз.

$$\begin{aligned} x^{2} &-2 x y+y^{2} \quad \color{Red} \text{ Original Expression. } \\ &=(\;\;)^{2}-2(\;\;)()+()^{2} \quad \color{Red} \text{ Replace variables with parenthesis. } \\ &=({\color{Red}-3})^{2}-2({\color{Red}-3})({\color{Red}2})+({\color{Red}2})^{2} \quad \color{Red} \text{ Substitute } -3 \text{ for } x \text{ and } 2 \text{ for } y \\ &=9-2(-3)(2)+4 \quad \color{Red} \text{ Evaluate exponenets first. } \\ &=9-(-6)(2)+4 \quad \color{Red} \text{ Left to right, multiply: } 2(-3)=-6\\ &=9-(-12)+4 \quad \color{Red} \text{ Left to right, multiply: } (-6)2=-12\\ &=9+12+4 \quad \color{Red} \text{ Add the opposite. } \\ &=25 \quad \color{Red} \text{ Add. }\\ \text{Thus, if } x=-3 \text{ and } y=2 \text{ , then } x^{2}-2 x y+y^{2}=25 \end{aligned} \nonumber$$

Вправа$\PageIndex{8}$

Якщо$x=-2$ і$y=-1$, оцініть$x^{3}-y^{3}$.

Відповідь

$-7$

Оцінка дробів

Якщо є рядок дробу, оцініть чисельник і знаменник окремо відповідно до Правил Керівного Порядку операцій, а потім виконайте поділ на кінцевому кроці.

Приклад$\PageIndex{9}$

Оцініть вираз $$\dfrac{ad-bc}{a+b} \nonumber$$ в$a=5, b=-3, c=2,$ і$d=-4$.

Рішення

Дотримуючись порад щодо оцінки алгебраїчних виразів, спочатку замініть усі входження змінних у виразі$(ad−bc)/(a+b)$ відкритими дужками. Далі підставляємо задані значення змінних ($5$$a$$-3$for$b$,$2$ for$c$, for і$-4$ for$d$) у відкриті дужки.

$$\begin{aligned} \dfrac{a d-b c}{a+b} &=\dfrac{(x)-(x)}{( )+( )} \\ &=\dfrac{({\color{Red}5})({\color{Red}-4}-)-({\color{Red}-3})({\color{Red}2})}{({\color{Red}5})+({\color{Red}-3})} \end{aligned} \nonumber$$

Нарешті, дотримуйтесь Правил Керівного порядку операцій, щоб оцінити отриманий вираз. Зверніть увагу, що ми оцінюємо вирази в чисельнику і знаменнику окремо, потім ділимо.

\ [\ почати {вирівняний}
\ dfrac {a d-b c} {a+b} &=\ dfrac {(x) - (x)} {() + ()}\ quad\ color {Red}\ text {Замініть змінні дужками.}\\
&=\ dfrac {({\ color {Червоний} 5}) ({\ color {Червоний} -4}) - {(\ колір {червоний} -3}) ({\ колір {червоний} 2})} {({\ колір {червоний} 5}) + ({\ колір {червоний} -3})}\ квадратний\ колір {червоний}\ текст { Замінити:} 5\ текст {для} a, -3\ текст {для} b, 2\ текст {для} c, -4\ текст {для} d\\
&=\ dfrac {-20- (-6)} {2}\ quad\ колір {червоний}\ текст {чисельник:} (5) (-4) =-20, (-3) (2) =-6\ текст {, знаменник:} 5+ (-3) =2\
&=\ dfrac {-20+6} {2}\ quad\ color {Червоний}\ text {чисельник: Додайте навпроти.}\\
&=\ dfrac {-14} {2}\ quad\ color {Червоний}\ текст {Чисельник:} -20+6 = -14\\
&=-7\ quad\ color {Червоний}\ текст {Розділити}\
\ текст {Таким чином, якщо} x = -3\ текст {і} y=2\ текст {, то} x^ {2} -2 x y^ y+y^ {2} =25
\ кінець {вирівняний}\ nonumber\]

Вправа$\PageIndex{9}$

Якщо$a=-7, b=-3, c=-15$ і$d=-14$, оцініть:$\dfrac{a^{2}+b^{2}}{c+d}$

Відповідь

$-2$

Використання графічного калькулятора

Графічний калькулятор є чудовим інструментом для оцінки алгебраїчних виразів, особливо коли числа, що беруть участь, великі.

Приклад$\PageIndex{10}$

Скористайтеся калькулятором графіків, щоб спростити наступний вираз: $$-213-35[-18-211(15-223)] \nonumber$$

Рішення

Перша складність цього виразу полягає в тому, що графічний калькулятор не має символу дужок для цілей групування. Калькулятор має лише дужки для групування. Отже, ми спочатку перетворюємо наш вираз на наступне:

$$-213-35(-18-211(15-223)) \nonumber$$

Зверніть увагу, що дужки і дужки повністю взаємозамінні. Наступна складність - визначення того, які з мінусових знаків є символами заперечення, а які - символами віднімання. Якщо знак мінус не з'являється між двома числами, це символ заперечення. Якщо знак мінус з'являється між двома числами, це символ віднімання. Отже, ми вводимо наступні натискання клавіш на нашому калькуляторі. Результат показаний на малюнку$\PageIndex{1}$.

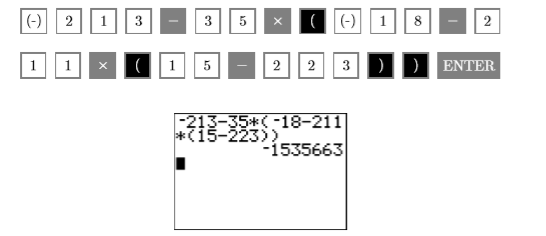
Малюнок$\PageIndex{1}$: Обчислення$-213-35[-18-211(15-223)]$

Таким чином,$-213-35[-18-211(15-223)]=-1,535,663$.

Вправа$\PageIndex{10}$

Скористайтеся графічним калькулятором для оцінки: $$-2-2[-2-2(-2-2)] \nonumber$$

Відповідь

$-14$

Приклад$\PageIndex{11}$

Скористайтеся графічним калькулятором для оцінки: $$\dfrac{5+5}{5+5} \nonumber$$

Рішення

Ви можете запитати: «Навіщо нам потрібен калькулятор для оцінки цього надзвичайно простого виразу?» Адже обчислити це дуже просто.

$$\begin{aligned} \dfrac{5+5}{5+5} &=\dfrac{10}{10} \quad \color{Red} \text{ Simplify numerator and denominator. } \\ &=1 \quad \color{Red} \text{ Divide: } 10/10=1 \end{aligned} \nonumber$$

Що ж, давайте введемо вираз$5+5/5+5$ в калькулятор і подивимося, наскільки добре ми розуміємо правила керівного порядку операцій (див. Перше зображення на малюнку$\PageIndex{2}$). Вау! Як вийшов калькулятор$11$? Відповідь повинна бути$1$! Давайте сповільнимо і застосуємо правила, що керують порядком операцій до виразу$5+5/5+5$.

$$\begin{aligned} \dfrac{5+5}{5+5} &= 5+\dfrac{5}{5}+5 \quad \color{Red} \text{ Divide first. } \\ &=5+1+5 \quad \color{Red} \text{ Divide: } \dfrac{5}{5}=1 \\ &= 11 \quad \color{Red} \text{ Add: } 5+1+5=11 \end{aligned} \nonumber$$

Ага! Ось так і потрапив калькулятор$11$.

$$5+5 / 5+5 \quad \text { is equivalent to } \quad 5+\dfrac{5}{5}+5 \nonumber$$

Давайте змінимо порядок оцінки за допомогою угруповання символів. Зверніть увагу, що:

$$\begin{aligned} (5+5) /(5+5) &=10 / 10 \quad \color{Red} \text { Parentheses first. } \\ &= 1 \quad \color{Red} \text { Divide: } 10/10 = 1 \end{aligned} \nonumber$$

Тобто:

$$(5+5) /(5+5) \quad \text { is equivalent to } \quad \dfrac{5+5}{5+5} \nonumber$$

Введіть$(5+5)(5+5)$ і натисніть клавішу ENTER, щоб отримати результат, показаний на другому зображенні на малюнку$\PageIndex{2}$).

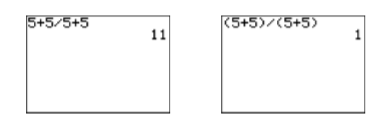
Малюнок$\PageIndex{2}$): Розрахунок$\dfrac{5+5}{5+5}$

Вправа$\PageIndex{11}$

Скористайтеся графічним калькулятором для оцінки: $$\dfrac{10+10}{10+10} \nonumber$$

Відповідь

$1$

Калькулятор графіків має місця пам'яті, доступні для «зберігання» значень. Вони написані літерами A-Z і з'являються на корпусі калькулятора, в алфавітному порядку при переміщенні зліва направо і вниз по клавіатурі. Зберігання значень у цих місцях пам'яті є ефективним способом оцінки алгебраїчних виразів, що містять змінні. Використовуйте клавішу ALPHA для доступу до цих місць пам'яті.

Малюнок$\PageIndex{3}$): Верхня половина ТІ-84.

Приклад$\PageIndex{12}$

Використовуйте графічний калькулятор для оцінки$|a|-|b|$ в$a=-312$ і$b=-875$.

Рішення

Спочатку зберігайте$-312$ у змінній$A$ наступними натисканнями клавіш. Щоб вибрати букву$A$, натисніть клавішу ALPHA, потім клавішу MATH, розташовану у верхньому лівому куті калькулятора (див. Рис.$\PageIndex{3}$).

Далі зберігаємо$-875$ в змінній B наступними натисканнями клавіш. Щоб вибрати букву$B$, натисніть клавішу ALPHA, потім клавішу APPS.

Результати цих натискань наведені на першому зображенні на малюнку$\PageIndex{4}$.

Тепер нам потрібно ввести вираз |a|−| b|. Функція абсолютного значення знаходиться в меню MATH. Коли ви натиснете клавішу MATH, ви помітите підменю MATH, NUM, CPX та PRB у верхньому рядку меню MATH. Клавішею зі стрілкою вправо виберіть підменю NUM (див. Друге зображення на малюнку$\PageIndex{4}$). Зауважте, що abs (є першим записом у цьому меню. Це функція абсолютного значення, необхідна для цього прикладу. Введіть вираз$\operatorname{abs}(\mathrm{A})-\operatorname{abs}(\mathrm{B})$, як показано на третьому зображенні на малюнку$\PageIndex{4}$. Використовуйте клавішу ALPHA, як описано вище, щоб ввести змінні A і B і закрити дужки за допомогою клавіші правої дужки з клавіатури. Натисніть клавішу ENTER, щоб оцінити ваш вираз.

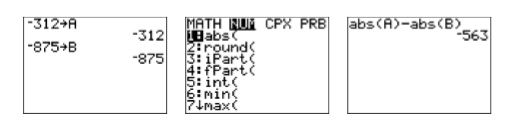
Малюнок$\PageIndex{4}$: Оцініть$|a|-|b|$ в$a=-312$ і$b=-875$.

Таким чином,$|a|-|b|=-563$.

Вправа$\PageIndex{12}$

Використовуйте графічний калькулятор для оцінки$|a-b|$ at $a=-312$ and $b=-875$.

Відповідь

$563$

Дописувачі

• Template:ContribElemAlgebraArnold