1.4: Десяткове позначення

Last updated
Save as PDF

Page ID: 58128

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Кожне раціональне число може бути виражено за допомогою десяткових позначень. Щоб змінити дріб в десятковий еквівалент, розділіть чисельник дробу на його знаменник. У деяких випадках процес завершиться, залишивши нульовий залишок. Однак в інших випадках залишки почнуть повторюватися, забезпечуючи десяткове уявлення, яке повторюється в блоках.

Приклад$\PageIndex{1}$

Змініть кожен з наступних дробів на десяткові.

$\dfrac{39}{80}$
$\dfrac{4}{11}$

Рішення

Ми виконуємо два ділення, одне зліва,$39/80$ щоб змінити на десяткове, одне праворуч, щоб знайти десяткове подання для$4/11$.

$рис. 1.4.1a.png$

Зліва процес ділення завершується нульовим залишком. Отже,$39/80 = 0.4875$ називається закінчувальним десятковим. Праворуч залишки повторюються за шаблоном, а частка також повторюється в блоках по два. Отже,$4 / 11=0.3636 \dots$ називається повторюваним десятковим. Ми також можемо використовувати повторювану смугу для написання$4 / 11=0 . \overline{36}$. Блок під повторюваною планкою повторюється нескінченно.

Вправа$\PageIndex{1}$

$24 /7$Змінити на десяткову.

Відповідь: $3 . \overline{428571}$

Навпаки, будь-який кінцевий десятковий може бути виражений у вигляді дробу. Вам потрібно лише порахувати кількість цифр після коми і використовувати таку ж кількість нулів у вашому знаменнику.

Приклад$\PageIndex{2}$

Висловіть кожне з наступних десяткових знаків у вигляді дробів. Зменшіть свої відповіді до найнижчих термінів.

$0.055$
$3.36$

Рішення

У кожному випадку підраховуйте кількість цифр після десяткової крапки і включіть рівну кількість нулів в знаменник.

У цьому прикладі є три цифри після десяткової крапки, тому ми розміщуємо число над$1000$, яке має три нулі після одиниці. \[\begin{aligned} 0.055 &=\dfrac{55}{1000} \\ &=\dfrac{11}{200} \end{aligned} \nonumber \]
У цьому прикладі є дві цифри після десяткової крапки, тому ми розміщуємо число над$100$, яке має два нулі після одиниці. \[\begin{aligned} 3.36 &=\dfrac{336}{100} \\ &=\dfrac{84}{25} \end{aligned} \nonumber \]

Вправа$\PageIndex{2}$

$0.45$Змінити на дріб. Знизити до найнижчих термінів.

Відповідь: $9/20$

Як ми бачили в прикладі $\PageIndex{1}$, повторюване$0. \overline{36}$ десяткове число еквівалентно дробу$4/11$. Дійсно, будь-який повторюваний десятковий може бути записаний як дріб. Наприклад,$0. \overline{3}=1 / 3$ і$0. \overline{142857}=1 / 7$. На майбутніх курсах ви навчитеся техніці зміни будь-якого повторюваного десяткового дробу на еквівалентний дріб. Однак не всі десяткові знаки закінчуються або повторюються. Наприклад, розглянемо десяткове число$0.42422422242222 \ldots$, яке ні закінчується, ні повторюється. Це число не може бути виражено за допомогою повторюваних рядкових позначень, оскільки кожна ітерація генерує одне додаткове$2$. Оскільки це число не повторюється і не закінчується, воно не може бути виражене як дріб. Значить,$0.42422422242222 \ldots$ є прикладом ірраціонального числа.

ірраціональні числа

Якщо число не може бути виражено у вигляді$p/q$, де$p$ і$q$ є цілими числами$q \neq 0$, то число називається ірраціональним числом.

Реальні числа

Включаючи всі раціональні та ірраціональні числа в одну множину, ми формуємо те, що відомо як множина дійсних чисел.

Набір дійсних чисел включає кожне число, яке ми будемо використовувати в цьому підручнику та курсі.

Додавання та віднімання десяткових знаків

При додаванні знакових десяткових знаків використовуйте ті самі правила, які ви навчилися використовувати при додаванні знакових цілих чисел або дробів.

Правила підпису для додавання

При додаванні двох десяткових чисел використовуйте наступні правила:

Щоб додати дві десяткові знаки з подібними знаками, додайте їх величини та префіксуйте їх загальний знак.
Щоб додати два десяткових знаків з несхожими знаками, відніміть меншу величину від більшого, а потім префіксуйте знак десяткового числа, що має більшу величину.

Приклад$\PageIndex{3}$

Спростити:

$-2.3+(-0.015)$
$-8.4+6 .95$

Рішення

У цій задачі зверніть увагу, що у нас є подібні ознаки. Отже, ми додаємо величини і префіксуємо загальний знак. \[-2.3+(-0.015)=-2.315 \nonumber \]\[\begin{array}{r}{2.300} \\ {+0.015} \\ \hline 2.315\end{array} \nonumber \]
У цій задачі зверніть увагу, що у нас несхожі ознаки. Таким чином, ми спочатку віднімаємо меншу величину від більшої величини, потім префіксуємо знак десяткового числа з більшою величиною. \[-8.4+6.95=-1.45 \nonumber\]\[\begin{array}{r}{8.40} \\ {-6.95} \\ \hline 1.45\end{array} \nonumber \]

Значить,$-2.3+(-0.015) =-2.315$ і$-8.4+6 .95 = -1.45$

Вправа$\PageIndex{3}$

Спростити:$-22.6+18.47$.

Відповідь: $-4.13$

Віднімання все ще означає «додати протилежне».

Приклад$\PageIndex{4}$

Спростити:

$-5.6-8.4$
$-7.9-(-5.32)$

Рішення

У цій задачі спочатку додамо протилежне. Тоді відзначимо, що у нас є подібні знаки. Отже, ми додаємо величини і префіксуємо загальний знак. \[\begin{aligned}-5.6-8.4 &=-5.6+(-8.4) \\ &=-14.0 \end{aligned} \nonumber\]\[\begin{array}{r}{5.6} \\ {+8.4} \\ \hline 14.0\end{array} \nonumber \]
У цій задачі спочатку додамо протилежне. Тоді відзначимо, що у нас несхожі ознаки. Таким чином, ми спочатку віднімаємо меншу величину від більшої величини, потім префіксуємо знак десяткового числа з більшою величиною. \[\begin{aligned}-7.9-(-5.32) &=-7.9+5.32 \\ &=-2.58 \end{aligned} \nonumber\]\[\begin{array}{r}{7.90} \\ {-5.32} \\ \hline 2.58\end{array} \nonumber \]

Значить,$-5.6-8.4=-14.0$ і$-7.9-(-5.32) = -2.58$.

Вправа$\PageIndex{4}$

Спростити:$-22.6-18.47$.

Відповідь: $-41.07$

Множення та ділення десяткових знаків

Правила знаків для десяткового множення та ділення такі ж, як і правила знаків, що використовуються для цілих чисел і дробів.

Знак Правила множення і ділення

При множенні або діленні двох десяткових чисел використовуйте наступні правила:

Подібні прикмети дають позитивний результат.
На відміну від знаків дають негативний результат

Множення десяткових чисел досить просто. Спочатку помножте величини чисел, ігноруючи десяткові крапки, потім підрахуйте кількість цифр праворуч від десяткової крапки в кожному множнику. Поставте десяткову крапку у добутку так, щоб кількість знаків праворуч від десяткових знаків дорівнювала сумі кількості цифр праворуч від десяткової крапки в кожному множнику.

Приклад$\PageIndex{5}$

Спростити:$(-1.96)(2.8)$.

Рішення

Помножте величини. Перше десяткове число має дві цифри праворуч від десяткової крапки, друге - одна цифра праворуч від десяткової крапки. Таким чином, ми повинні розмістити в цілому три цифри праворуч від десяткової крапки в добутку.

\[(-1.96)(2.8)=-5.488 \nonumber \]

\[\begin{array}{r}{1.96} \\ { \times 2.8} \\ \hline 1568 \\ {392\;\;} \\ \hline 5.488\end{array} \nonumber \]

Відзначимо, що на відміну від ознак виходить негативний продукт.

Вправа$\PageIndex{5}$

Спростити:$(-12.5)(-23.4)$.

Відповідь: $292.50$

При діленні знакових десяткових чисел ігноруйте знаки і діліть величини. Натисніть десяткову крапку в дільнику до кінця дільника, потім перемістіть десяткову крапку в дивіденді на рівну кількість пробілів. Це встановлює десяткову крапку в частці.

Приклад$\PageIndex{6}$

Спростити:$-4.392 \div(-0.36)$.

Рішення

Розділіть величини. Перемістіть десяткове число в дільнику до кінця дільника. Перемістіть десяткове число в дивіденді на рівну кількість знаків (два місця) вправо.

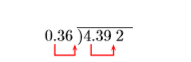
$рис. 1.4.1b.png$

Помістіть десяткову крапку в частку безпосередньо над новою позицією десяткової крапки в дивіденді, а потім розділіть.

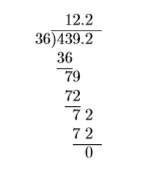
$рис. 1.4.1c.png$

Подібні ознаки дають позитивний результат. Отже,$-4.392 \div(-0.36)=12.2$.

Вправа$\PageIndex{6}$

Спростити:$-5.76 / 3.2$.

Відповідь: $-1.8$

Порядок операцій

Десяткові числа підпорядковуються тим самим Правилам, що і цілі числа та дроби.

Правила, що керують порядком операцій

При оцінці виразів дійте в наступному порядку.

Спочатку оцініть вирази, що містяться в угрупованні символів. Якщо символи групування вкладені, спочатку оцініть вираз у внутрішній парі символів групування.
Оцінити всі показники, які з'являються у виразі.
Виконуйте всі множення і ділення в тому порядку, щоб вони відображалися у виразі, рухаючись зліва направо.
Виконуйте всі додавання і віднімання в тому порядку, щоб вони відображалися у виразі, рухаючись зліва направо.

Приклад$\PageIndex{7}$

Дано$x=-0.12$, оцініть$-x^{2}$.

Рішення

Дотримуючись порад щодо оцінки алгебраїчних виразів, спочатку замініть усі входження змінної$x$ у виразі$-x^2$ відкритими дужками. Далі$-0.12$ підставляємо$x$ в відкриті дужки, потім спрощуємо.

\[\begin{aligned} -x^{2} &=-(\quad)^{2} \quad \color{Red} \text { Replace } x \text { with open parentheses. } \\ &=-(-0.12)^{2} \quad \color{Red} \text { Substitute }-0.12 \text { for } x . \\ &=-(0.0144) \quad \color{Red} \text { Exponent: }(-0.12)^{2}=0.0144 \\ &=-0.0144 \quad \color{Red} \text { Negate. } \end{aligned} \nonumber \]

Зверніть увагу, що спочатку ми квадратично, потім заперечуємо друге. Таким чином, якщо$x = -0.12$, то$-x^{2}=-0.0144$.

Вправа$\PageIndex{7}$

З огляду на$y=-0.2$, оцініть:$-y^{4}$.

Відповідь: $-0.0016$

Приклад$\PageIndex{8}$

Дано$x=-0.3$, оцініть$1.2 x^{2}-3.4 x$.

Рішення

Дотримуючись порад щодо оцінки алгебраїчних виразів, спочатку замініть усі входження змінної$x$ у виразі$1.2 x^{2}-3.4 x$ відкритими дужками. Далі$-0.3$ підставляємо$x$ в відкриті дужки, потім спрощуємо.

\[\begin{aligned} 1.2 x^{2}-3.4 x &=1.2(\quad)^{2}-3.4(\quad) \quad \color{Red} \text { Replace } x \text { with parentheses. } \\ &=1.2(-0.3)^{2}-3.4(-0.3) \quad \color{Red} \text { Substitute }-0.3 \text { for } x . \\ &=1.2(0.09)-3.4(-0.3) \quad \color{Red} \text { Exponent: }(-0.3)^{2}=0.09 \\ &=0.108-(-1.02) \quad \color{Red} \text { Multiply: } 1.2(0.09)=0.108 \text { and } \\ &=0.108+1.02 \quad \color{Red} \text { Add the opposite. } \\ &=1.128 \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]

Таким чином, якщо$x = -0.3$, то$1.2 x^{2}-3.4 x=1.128$.

Вправа$\PageIndex{8}$

З огляду$y=-0.15$ на,$\text { evaluate: } -1.4 y^{2}+2.2 y $.

Відповідь: $-0.3615$

Ми бачили раніше, що ми можемо змінити дріб на десятковий шляхом ділення.

Приклад$\PageIndex{9}$

Дано$x=2 / 5$, оцініть$-3.2 x+5$.

Рішення

Дотримуючись порад щодо оцінки алгебраїчних виразів, спочатку замініть усі входження змінної$x$ у виразі$-3.2x+5$ відкритими дужками. Далі$2/5$ підставляємо$x$ в відкритих дужках.

\[\begin{aligned} -3.2 x+5 &=-3.2(\; )+5 \quad \color{Red} \text { Replace } x \text { with open parentheses. } \\ &=-3.2\left(\dfrac{2}{5}\right)+5 \quad \color{Red} \text { Substitute } 2 / 5 \text { for } x \end{aligned} \nonumber \]

Один з підходів полягає$2/5$ в зміні на десятковий шляхом ділення чисельника на знаменник. Таким чином,$2/5=0 .4$.

\[\begin{aligned} &=-3.2(0.4)+5 \quad \color{Red} {\text { Replace } 2 / 5 \text { with } 0.4} \\ &=-1.28+5 \quad \color{Red} \text { Multiply: }-3.2(0.4)=-1.28 \\ &=3.72 \quad \color{Red} \text { Add: }-1.28+5=3.72 \end{aligned} \nonumber \]

Таким чином, якщо$x =2 /5$, то$-3.2x+5=3 .72$.

Вправа$\PageIndex{9}$

Дано$y=-3 / 4$, оцініть$-2.3 y+7$.

Відповідь: $8.725$

Як ми бачили в прикладі $\PageIndex{2}$, ми можемо легко змінити закінчення десяткового дробу, помістивши число (без десяткової крапки) над належною степеню десяти. Вибір степені десяти повинен збігатися з кількістю цифр праворуч від десяткової крапки. Наприклад:

\[0.411=\dfrac{411}{1000} \quad \text { and } \quad 3.11=\dfrac{311}{100} \quad \text { and } \quad 15.1111=\dfrac{151111}{10000} \nonumber \]

Зверніть увагу, що кількість нулів у кожному знаменнику відповідає кількості цифр праворуч від десяткової крапки.

Приклад$\PageIndex{10}$

Дано$y =-0.25$, оцініть$-\dfrac{3}{5} y+4$.

Рішення

Дотримуючись порад щодо оцінки алгебраїчних виразів, спочатку замініть усі входження змінної$y$ у виразі$-(3/5)y+4$ відкритими дужками. Далі$-0.25$ підставляємо$y$ в відкритих дужках.

\[\begin{aligned} -\dfrac{3}{5} y+4 &=-\dfrac{3}{5}(\quad)+4 \quad \color{Red} \text { Replace } y \text { with open parentheses. } \\ &=-\dfrac{3}{5}(-0.25)+4 \quad \color{Red} \text { Substitute }-0.25 \text { for } y \end{aligned} \nonumber \]

Місце$25$ над,$100$ щоб визначити$-0.25 = -25/100$, що, або після скорочення,$-0.25 =-1/4$.

\ [\ почати {вирівняний}
&=-\ dfrac {3} {5}\ ліворуч (-\ dfrac {1} {4}\ праворуч) +4\ квадратний\ колір {червоний}\ текст {Замінити} -0.25\ текст {з} -1/4\
&=\ dfrac {3} {20} +4\ квадратний\ колір {Червоний}\ текст {Множення:} -\ dfrac {3}} {5}\ ліворуч (-\ dfrac {1} {4}\ праворуч) =\ dfrac {3} {20}\
&=\ dfrac {3} {20} +\ dfrac {80} {20}\ quad\ color {Червоний}\ text {Зробити еквівалентні дроби за допомогою РК-дисплея.}\\
&=\ dfrac {83} {20}\ quad\ color {Червоний}\ текст {Додати.}
\ кінець {вирівняний}\ nonumber\]

Таким чином, якщо$y =-0.25$, то$-(3 / 5) y+4=83 / 20$.

Вправа$\PageIndex{10}$

З огляду на$z=-0.4$, оцініть:$5-\dfrac{4}{5} z$.

Відповідь: $133/25$

Округлення за допомогою графічного калькулятора

Ось алгоритм округлення десяткового числа до певного місця.

Правила округлення

Щоб округлити число до певного місця, виконайте наступні дії:

Позначте місце, яке ви хочете округлити. Цифра в цьому місці називається цифрою округлення.
Відзначте цифру в місці, розташованому праворуч від округлення цифри. Це називається тестовою цифрою.
1. Якщо контрольна цифра більше або дорівнює$5$, додайте$1$ до округлення цифру, після чого всі цифри праворуч від округлення замініть нулями. Кінцеві нулі праворуч від десяткової крапки можуть бути вилучені.
2. Якщо контрольна цифра менше$5$, цифру округлення тримайте однаковою, потім всі цифри праворуч від округлення замініть нулями. Кінцеві нулі праворуч від десяткової крапки можуть бути вилучені.

Приклад$\PageIndex{11}$

Використовуйте графічний калькулятор для оцінки$125 x^{3}-17.5 x+44.8$ на$x = -3.13$. Округлите відповідь до найближчої десятої.

Рішення

По-перше,$-3.13$ збережіть у змінній$X$ наступними натисканнями клавіш.

$рис. 1.4.1d.png$

Результат показаний на першому зображенні на малюнку$\PageIndex{1}$. Далі вводимо вираз$125 x^{3}-17.5 x+44.8$ наступними натисканнями клавіш.

$рис. 1.4.1e.png$

Результат показаний на другому зображенні на рис$\PageIndex{1}$. Таким чином, відповідь приблизно$-3733.462125$. Тепер нам потрібно округлити цю відповідь до найближчої десятої. Відзначте цифру округлення на десятому місці і контрольну цифру праворуч від неї.

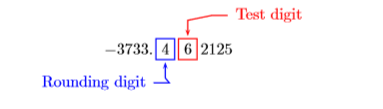
$рис. 1.4.1f.png$

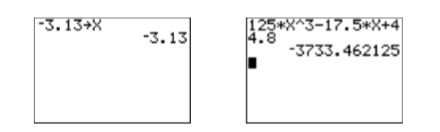
$рис. 1.4.1.png$

Малюнок$\PageIndex{1}$: Оцініть$125 x^{3}-17.5 x+44.8$ на$x=-3.13$

Оскільки тестова цифра більше або дорівнює$5$, додайте$1$ до округлення цифру, після чого всі цифри праворуч від округлення замініть нулями.

\[-3733.462125 \approx-3733.500000 \nonumber \]

Вилучити кінцеві нулі з кінця дробової частини десяткової. Це не змінює значення нашої відповіді.

\[-3733.462125 \approx-3733.5 \nonumber \]

Тому якщо$x =-3.13$. то до найближчої десятої:

\[125 x^{3}-17.5 x+44.8 \approx-3733.5 \nonumber \]

Вправа$\PageIndex{11}$

Оцініть$x^{3}-3 x$ за адресою$x =-1.012$. Округлити до найближчої сотої.

Відповідь: $2.0$

Дописувачі

Template:ContribElemAlgebraArnold