4.4: Трансформації

Last updated
Save as PDF

Page ID: 58778

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Існує три основних типи перетворення, які ми розглянемо:
1) Горизонтальні та вертикальні зрушення
2) Відображення над$y$ осі$x$ або
3) Горизонтальні та вертикальні розтяжки
Якщо взяти задану функцію, скажімо,$f(x)=x,$ тоді це має графік, який ми бачимо нижче - пряма лінія з нахилом 1 і$y$ -перехоплення$0 .$ Якщо ми додамо до функції,$f(x)+6=x+6,$ то це додасть 6 до всіх$y$ -значень, які зрушують графік 6 місцями вгору.

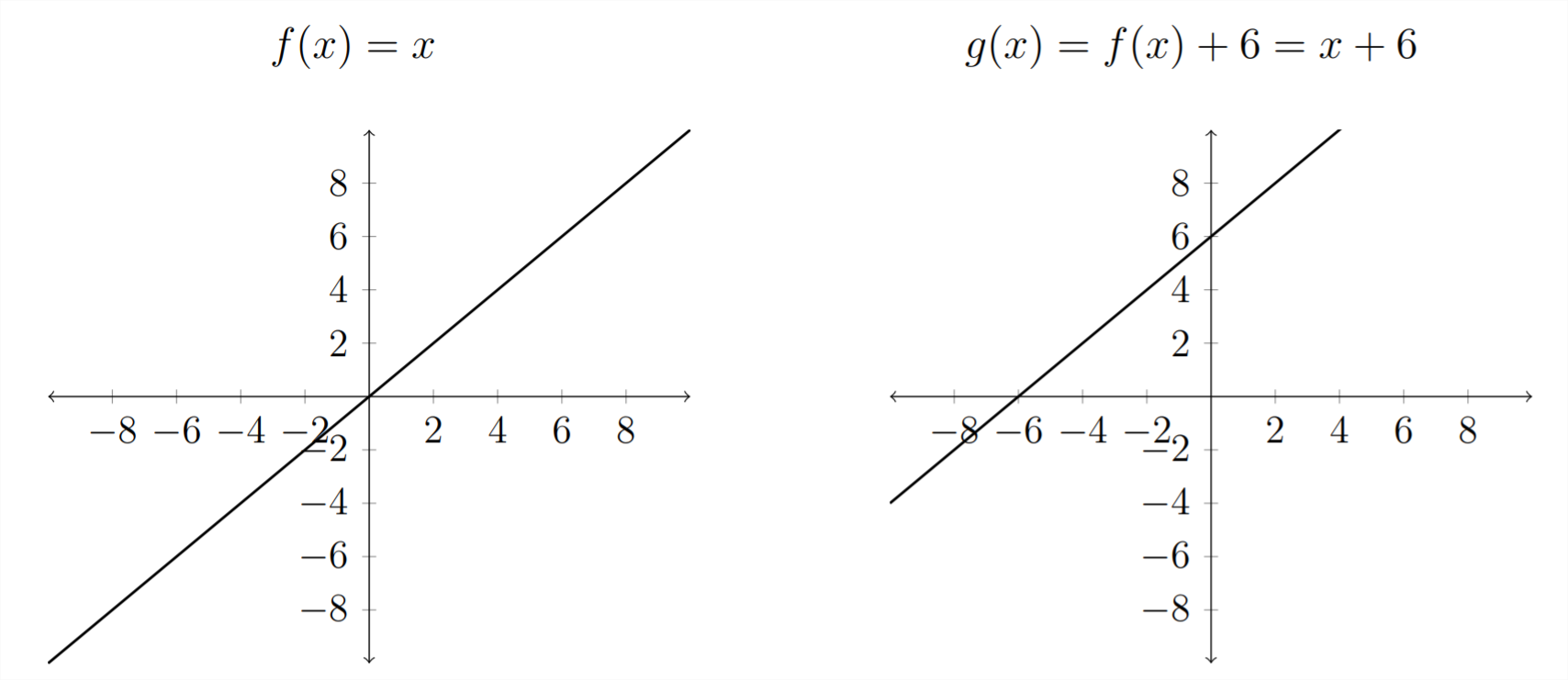
$clipboard_edb94f846b02456aeaf26cb9d5d4ae93a.png$

Вертикальні зсуви
Отже, якщо у нас є загальна функція,$f(x)$ яка описується графіком, ми можемо визначити графік для$f(x)+k,$ де$k$ є деяке число, яке буде$(\text { if } k>0)$ або зміщуватися$f(x)$ вгору або вниз (якщо$k<0$)
Наприклад, розглянемо наступний графік для$f(x)$
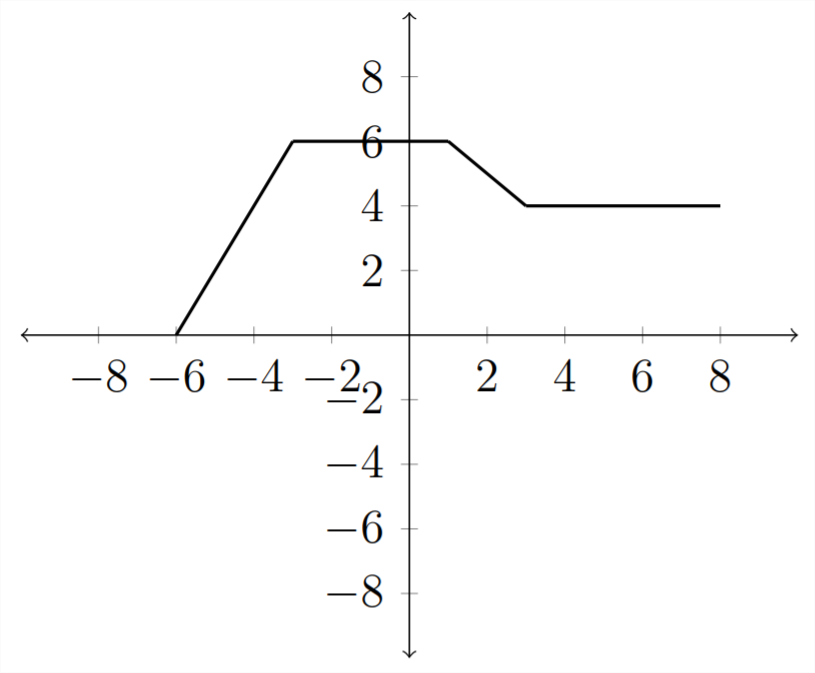
$clipboard_e1868c85fac715e9cc59d36869608e752.png$

Потім, якщо ми хочемо графік для$f(x)-2$, просто зсуньте всі$y$ -значення вниз на 2 місця:
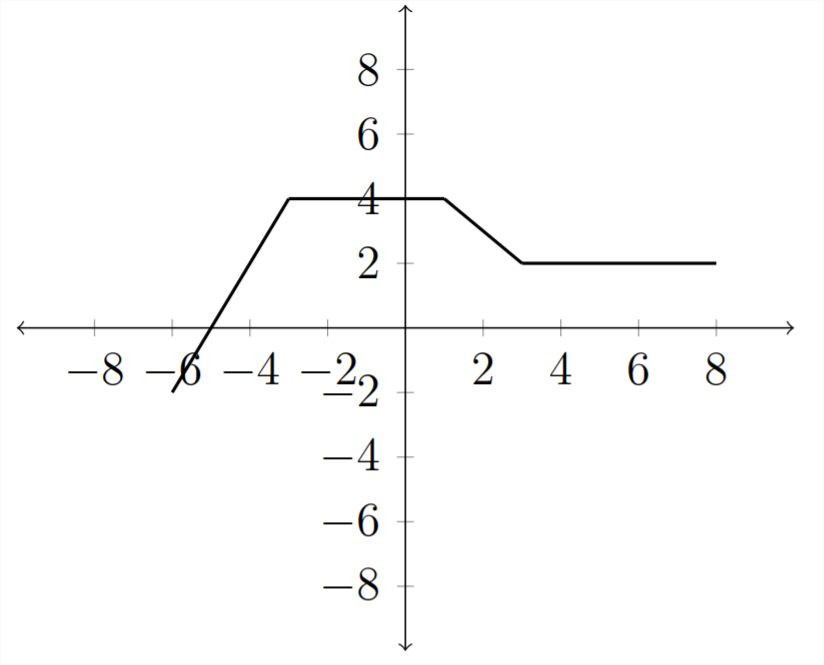
$clipboard_e384d64a193e49d8d61bd23533e44a9c5.png$
Це стандартне перетворення вертикального зсуву функції.

Горизонтальні
зсуви Функція також може бути зрушена горизонтально шляхом додавання або віднімання числа всередині дужок.
Якщо ми почнемо з нашої оригінальної функції$f(x)$
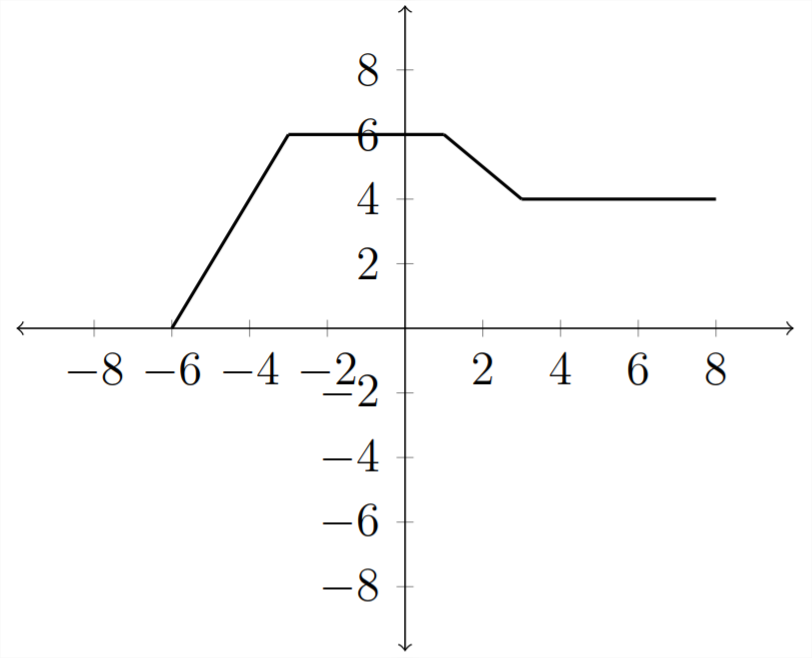
$clipboard_e0a58a36da1538d0151b00fc036bc5f2b.png$

Тоді перетворення$f(x-2)$ змістить графік горизонтально, за винятком того, що він буде рухатися в протилежну сторону знака. $f(x-2)$Зсув буде переміщати графік на 2 місця вправо, тоді як зсув$f(x+2)$ буде переміщати графік на 2 місця вліво.

Причина, чому це станеться, буде більш зрозумілою, якщо ми подивимося на таблицю значень для функції:
$clipboard_e3f5d56400b176ab907f8f40093fbc2c3.png$
Тепер, якщо замість$f(x),$ ми хочемо,$f(x-2),$ то ми додаємо ще один стовпець до таблиці:
$clipboard_e6edd92e2223e347c7bfb6507c763b105.png$
Зверніть увагу, що мати те ж саме$y$ -value як початковий графік, ми повинні пройти 2 місця праворуч, щоб після того, як ми віднімаємо 2 з$x$ -значення, ми повернемося до початкового$x$ -значення. Отже, графік$f(x-2)$ буде виглядати так:
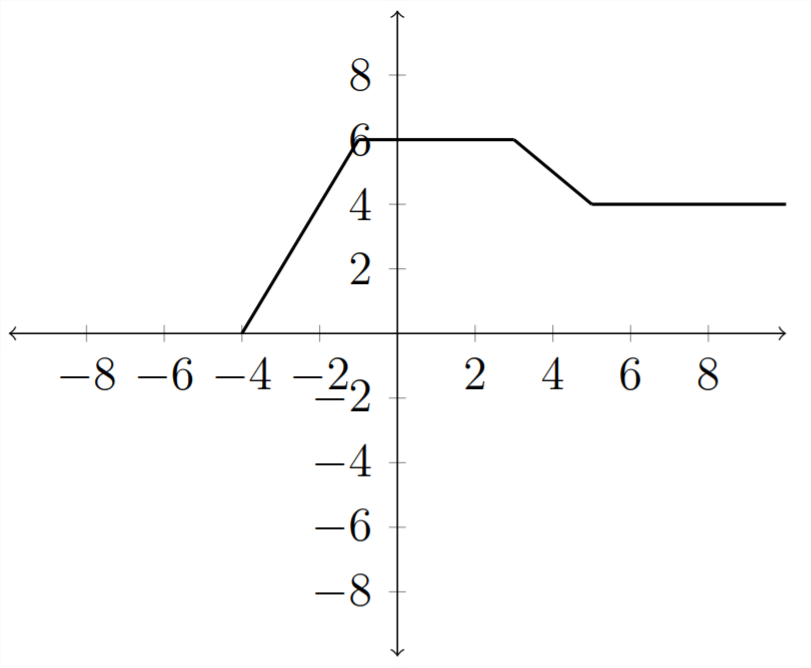
$clipboard_e7ab3b4b08959c213634cd486b7c18eb4.png$
Зверніть увагу, як значення на графіку збігаються зі значеннями в таблиці.

Відображення$y$ заперечення$x$ або значень функції матиме ефект відображення функції над$x$ віссю$y$ або. Якщо розглядати функцію$f(x)$ - ту саму, яку ми використовували в попередніх прикладах:
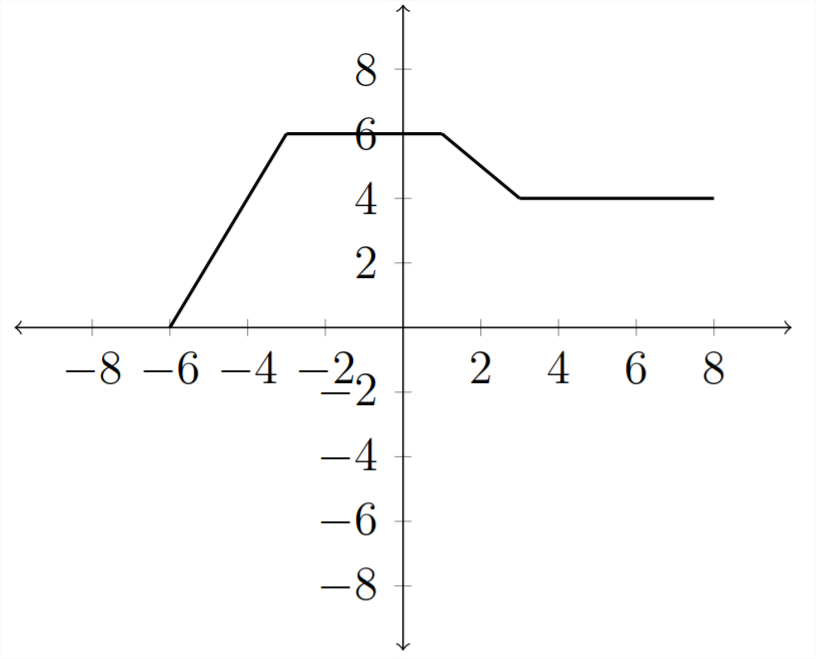
$clipboard_e347cd8db4203bc3a2a618eccde38de61.png$
Тоді графік$y=-f(x)$ буде відображатися над$x$ -віссю. Негативний знак перед функцією заперечує всі$y$ значення, відображаючи їх над$x$ -віссю. Давайте подивимося на це в таблиці значень:
$clipboard_e9dd6028bd7beb4188d4eec9848e996bf.png$
Отже, графік буде виглядати так: З іншого
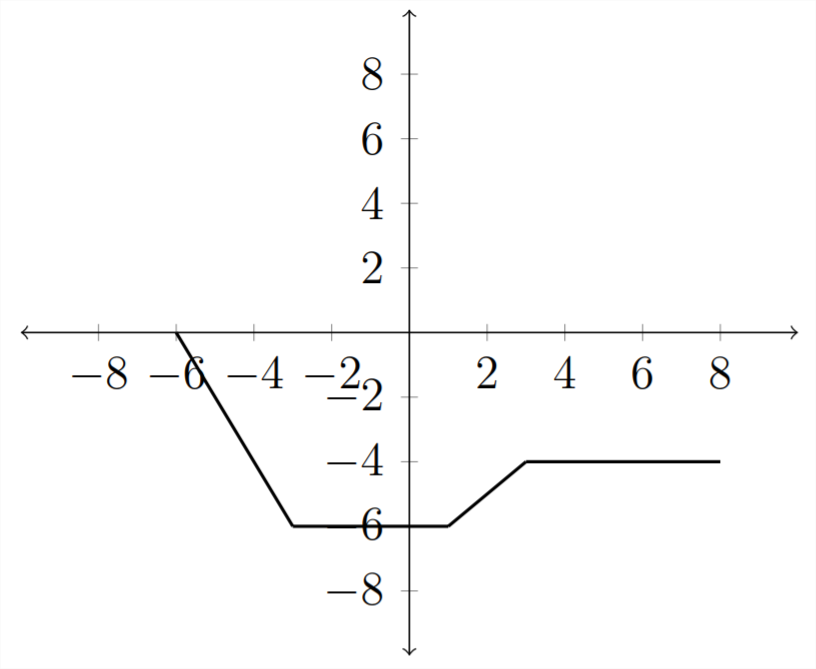
$clipboard_ec75725e96bda259ad5fbe6e863659f51.png$
боку, якщо ми заперечуємо$x$ -змінну$(f(-x)),$ то значення функції раніше пов'язані з позитивними значеннями $x$буде асоціюватися з від'ємними значеннями$x$ і навпаки. Це відобразило б функцію над$y$ -віссю.
Якщо ми знову розглянемо нашу вихідну функцію і таблицю значень:
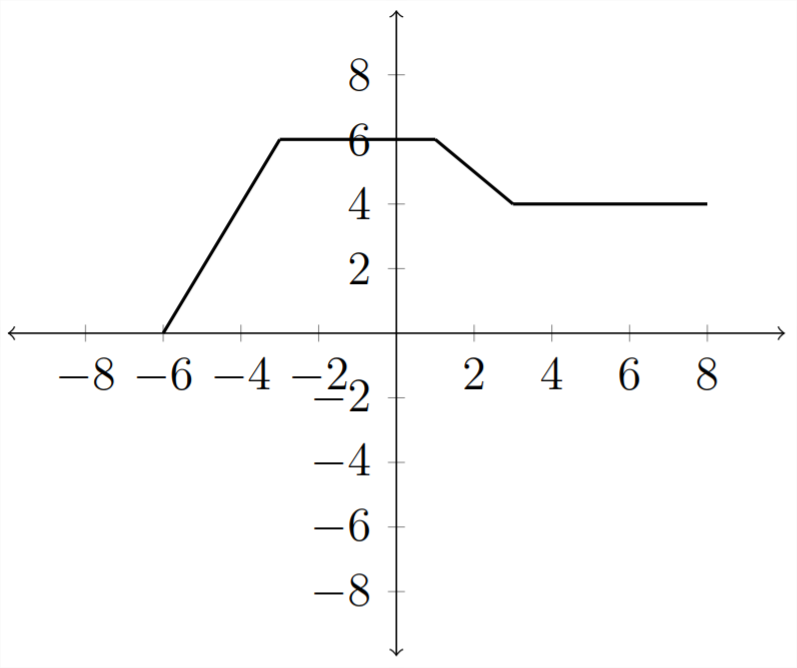
$clipboard_e64f52485364cf255f8cc8ba15f4f0fdb.png$
У таблиці:
$clipboard_e0ab871f54621ac5390d031306b8528ef.png$
І графік буде відображатися над$y$ -віссю:
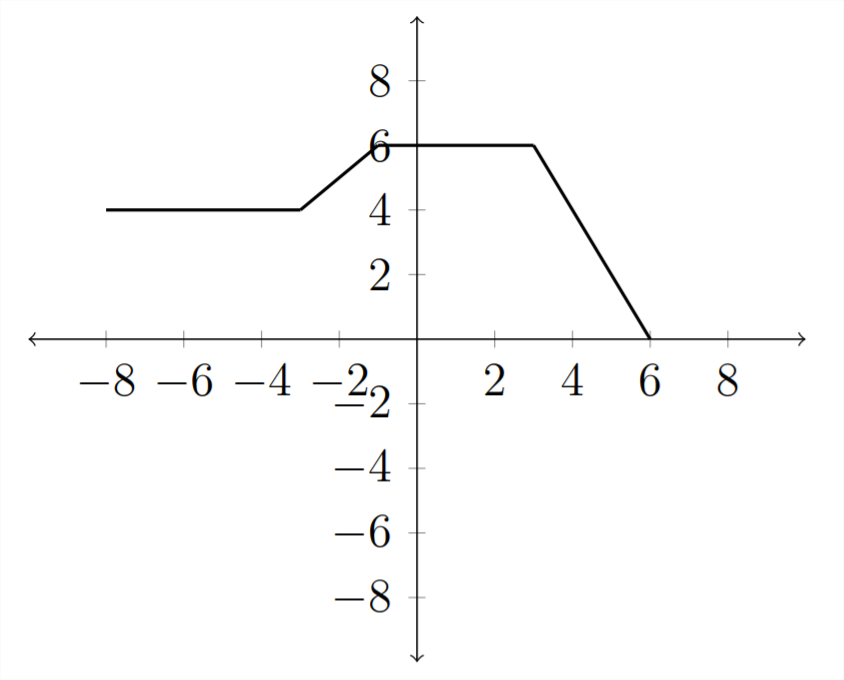
$clipboard_e6c4501bcd8113f99eba11ba445467c0d.png$

Розтягування і стиснення графіків

Останній тип перетворення, який ми розглянемо, - це розтягування або стиснення графіка шляхом множення всередині або поза дужками. Починаючи з нашого знайомого прикладу функції$y=f(x)$
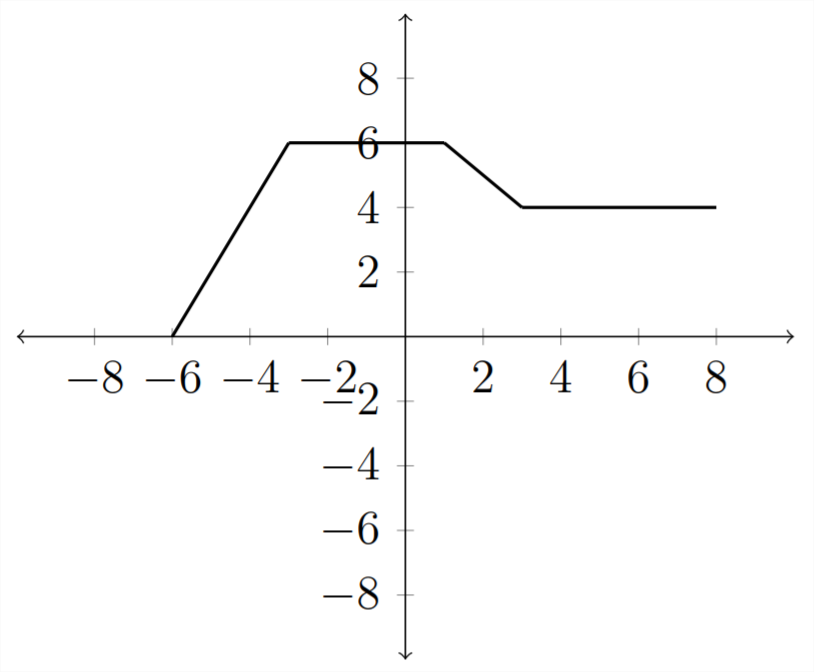
$clipboard_ee635edba8ef54a89bb7811cb6c266823.png$
Якщо помножити функцію на константу поза дужками:$y=2 f(x)$ то це матиме ефект множення всіх$y$ значень на$2 .$ В таблиці:
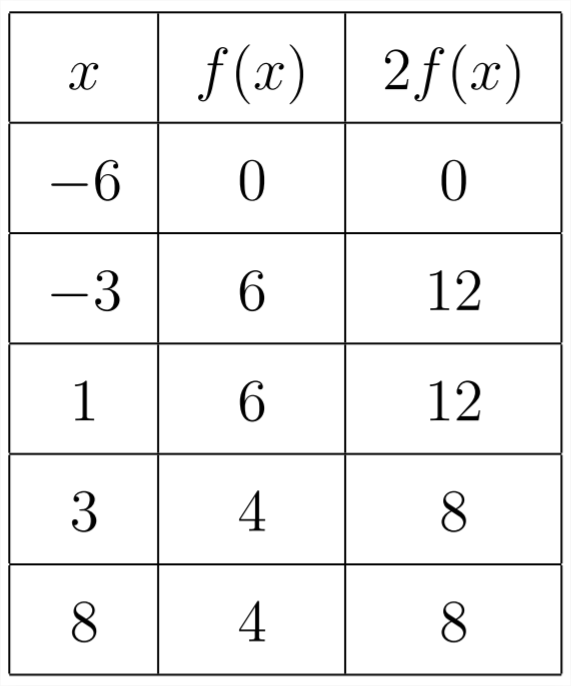
$clipboard_e21f2103671930d6dda497ea205cadf67.png$

Графік$y=2 f(x)$ виглядатиме так:
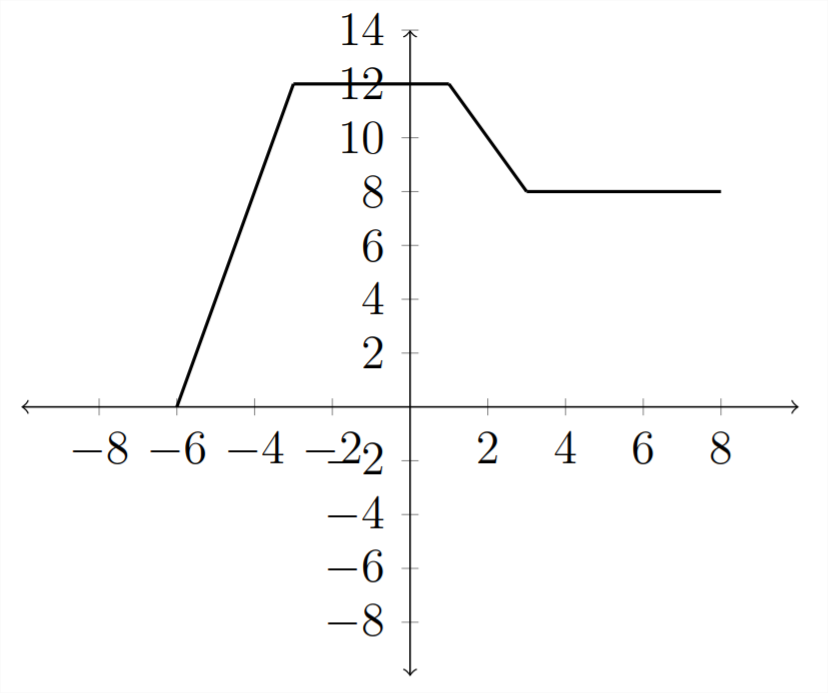
$clipboard_e921e2a2750a616f22f39cb90a3920425.png$
Аналогічним чином множення на число менше 1 стискає графік. Графік для$y=\frac{1}{2} f(x)$ наведено нижче:
$clipboard_e25e17cc193f3365e2d03e6efdf81864a.png$

Множення всередині дужок впливає на$x$ змінні.
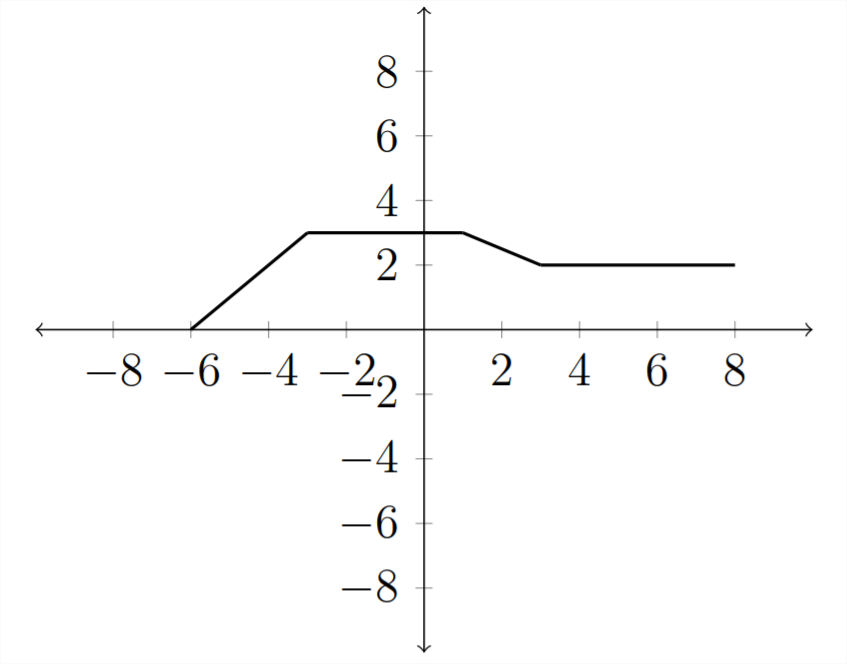
Якщо розглядати функцію$y=f(2 x)$, то це матиме ефект стиснення графіка уздовж$x$ -осі:
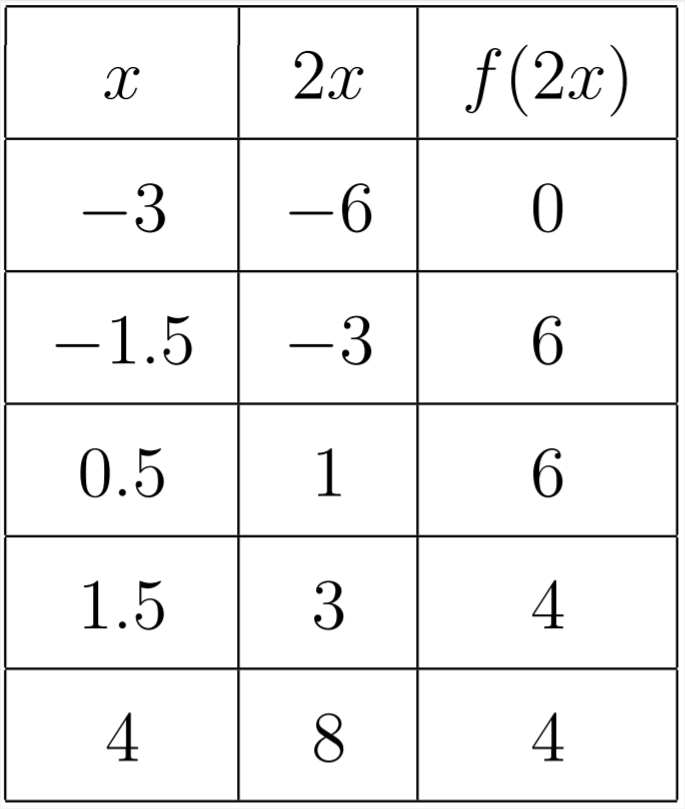
$clipboard_ef614db647c95609a575f1342bfd8177a.png$

Зверніть увагу, як кожне$x$ значення довелося скоротити навпіл так, що коли ми помножили його на 2, ми закінчилися з початковим$x$ значенням. Графік виглядатиме так:

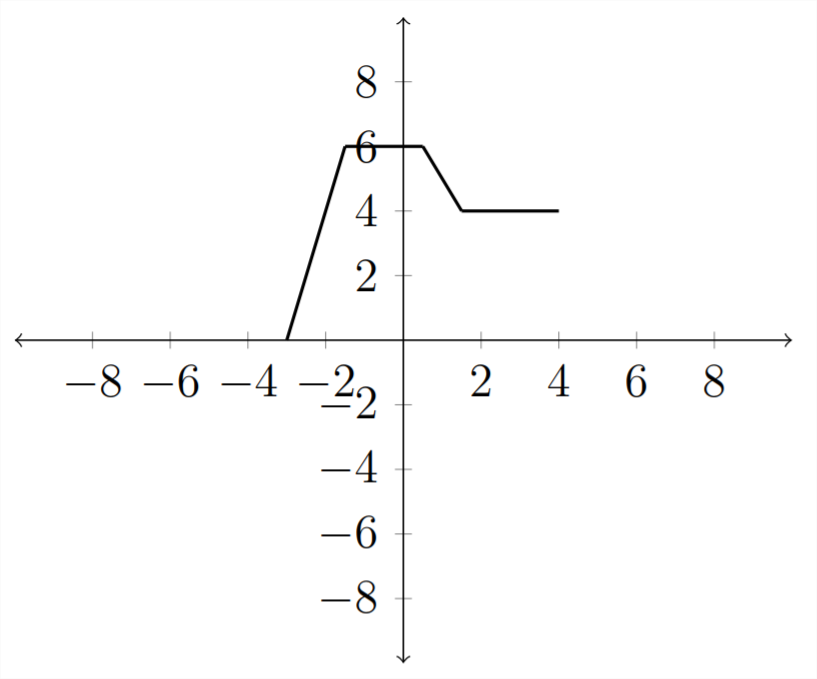
$clipboard_e61bc69029c85ba4a1b495259129bcf73.png$

Множення всередині дужок на число менше одиниці призведе до розтягування графіка.
$clipboard_e0e8e7f6a564fce4a37dca0e019782025.png$
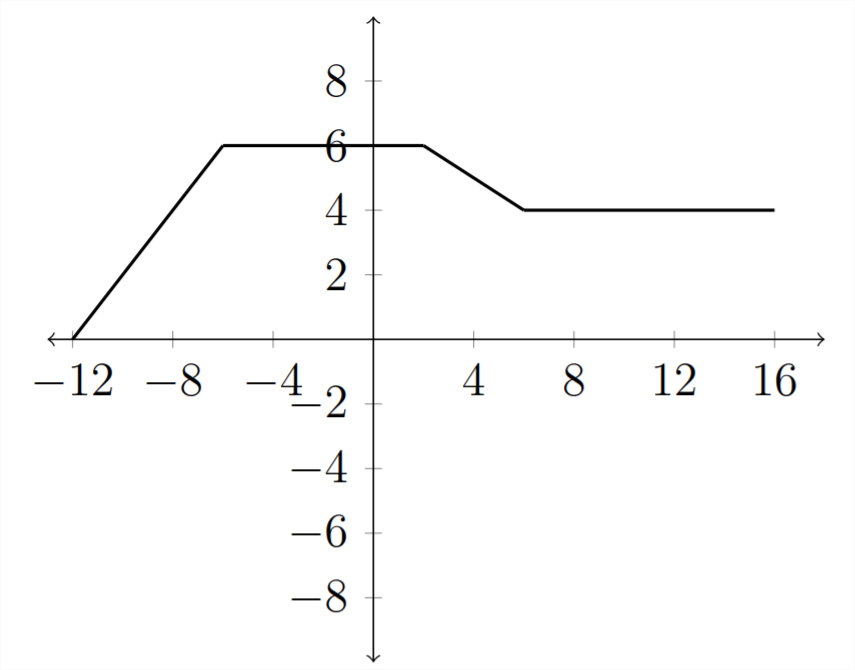
$clipboard_ef9392f4aa2d448f5c2b1adaec789aca2.png$
У цих прикладах ми розглядали лише одну трансформацію за раз. У вправах потрібно буде враховувати ефект відразу декількох перетворень.

Вправи 4.4
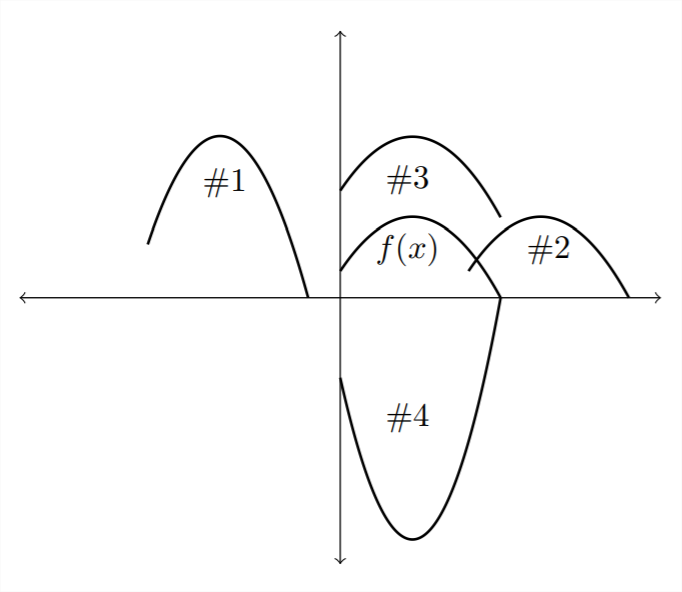
1) Зіставте кожну з функцій на графіку з відповідним перетворенням, описаним нижче.
а)$\quad f(x-4)$
б$\quad f(x)+3$
) в)$\quad -3 f(x)$
г)$\quad 2 f(x+6)$

$clipboard_e167d20f9d1498a9c40e7d33d1e23d22b.png$

2) Зіставте кожне з описів з відповідним перетворенням функції.

\ begin {масив} {cc}
a)\ quad y = f (x-1) & 1)\ text {Зсув ліворуч на одну одиницю}\\
b)\ quad y = f (x) -1 & 2)\ text {Віддзеркалити над$x$ -вісь, потім зрушення вліво на одну одиницю}\\
c)\ quad y=f (x) +1 & 3)\ текст {Зсув вправо на одну одиницю}\\
d)\ quad y=f (x+1) & 4) \ text {Віддзеркалити по$x$ -осі, потім зсунути вгору на одну одиницю}\\
e)\ quad y = f (-x) +1 & 5)\ text {Віддзеркалити над$x$ -вісь, потім зрушити вниз на одну одиницю}\\ f)\ quad y =
f (-x) -1 & 6)\ text {Зсув вниз на одну одиницю}\\ g)\ quad y = -f (x) +1 & 7)\ текст {Віддзеркалити над однією одиницею}\\
g)\ quad y = -f (x) +1 & 7)\ text {Віддзеркалити над $x$-вісь, відображати над$y$ -вісь, потім зсунути вгору на одну одиницю}\\
h)\ quad y = -f (x+1) & 8\ text {Зсув вліво на одну одиницю, відображати над$y$ -вісь, а потім зрушити вгору на одну одиницю}\\
i)\ quad y = -f (x) -1) & 9)\ text {Зсув вгору на одну одиницю}\\ j)\ quad y = f (-x) -1) & 9)\ text {Зсув вгору на одну одиницю}\\
j) +1) & 10)\ text {Віддзеркалити по$y$ -осі, потім зсунути вгору на одну одиницю}\\
k)\ quad y=-f (-x) & 11)\ text {Віддзеркалити над$y$ -осі, потім зсунути вниз на одну одиницю}\
\\ end {масив}

3) Зіставте кожен з описів з відповідним перетворення функції.
\ begin {масив} {cc}
a)\ quad y=f (x+2) +3 & 1)\ text {Зсув вліво 2 одиниці, потім зрушити вниз 3 одиниці}\\
b)\ quad y=f (x+3) +2 & 2)\ текст {Зсув вліво 3 одиниці, потім зсув вгору 2 одиниці}\\
c)\ quad y=f (x-2) +3 & 3)\ текст {Зсув вліво 3 одиниці, потім зрушення вгору 2 одиниці}\\
d)\ quad y = f (x-2) -3 & 4)\ text {Зсув вліво 3 одиниці, потім зрушити вниз 2 одиниці}\\
e)\ quad y=f (x+2) -3 & 5)\ text {Shift вправо 3 одиниці, потім зсув вниз 2 одиниці}\\
f)\ quad y=f (x-3) +2 & 6)\ text {Відображення над$y$ -віссю, потім зсув вгору 2 одиниці}\\
g)\ quad y = f (x-3) -2 & 7)\ text {Віддзеркалити над$x$ -осі, потім зрушити вправо 2 одиниці}\\
h)\ quad y = f (x+3) -2 & 8)\ text {Віддзеркалити над$x$ -вісь, потім зсунути вліво 2 одиниці}\\
i)\ quad y = -f (x+2) & 9)\ текст {Зсув вліво 2 одиниці, потім відображати над$y$ -осі}\\
j)\ quad y = -f (x-2) & 10)\ text {Shift вправо 2 одиниці, потім зрушення вгору 3 одиниці}\\
k)\ quad y=f (2-x) & 11)\ text {Shift вліво 2 одиниці, потім зрушення вгору 3 одиниці}
\\ quad y = f (-x) +2 & 12)\ текст {Зсув вправо 2 одиниці, потім зрушення вниз 3 одиниці}
\ end {масив}

Застосуйте перетворення, зазначені для кожної функції.
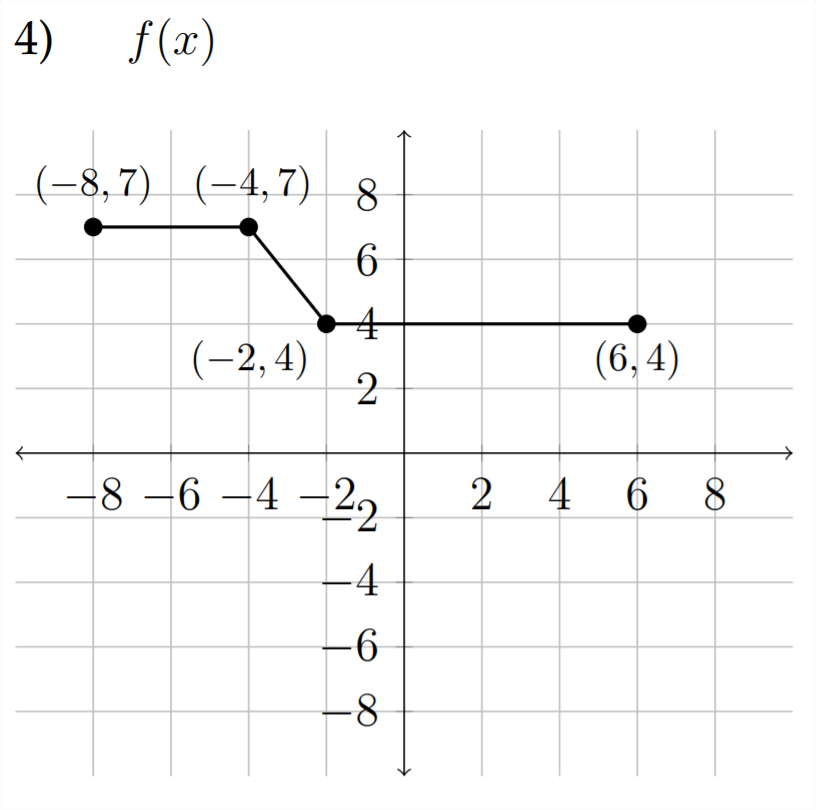
$clipboard_e763571b89dd30538d95b384b10a4bdf0.png$
а)$\quad f(x-3)$
б$\quad-f(x)+2$
) в)$\quad \frac{1}{2} f(x-1)$
г)$\quad f(-x)+1$
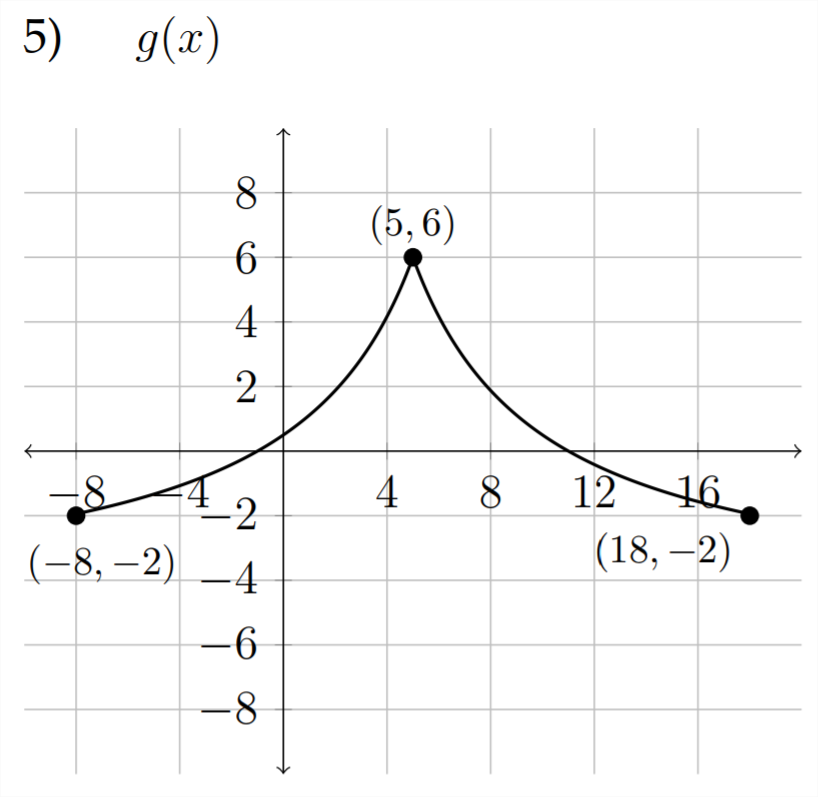
$clipboard_eaf108e96da326bd505a70cda92c9e49e.png$
а)$\quad g(x)-3$
б$\quad-g(x)-1$
) в)$\quad 2 g(x+2)$
г)$\quad g(2 x)-1$
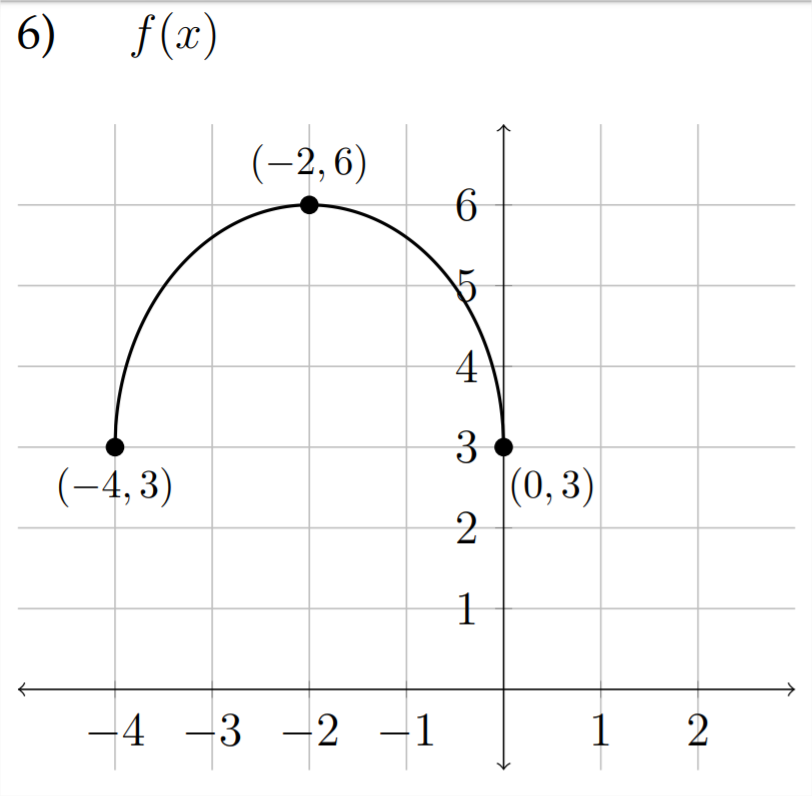
$clipboard_e7a2a4c14187e997b81b319f93be1f797.png$
а)$\quad f(x)+2$
б$\quad-f(x-1)$
) в)$\quad f(x-1)-3$
г)$\quad \frac{1}{3} f(x)+4$

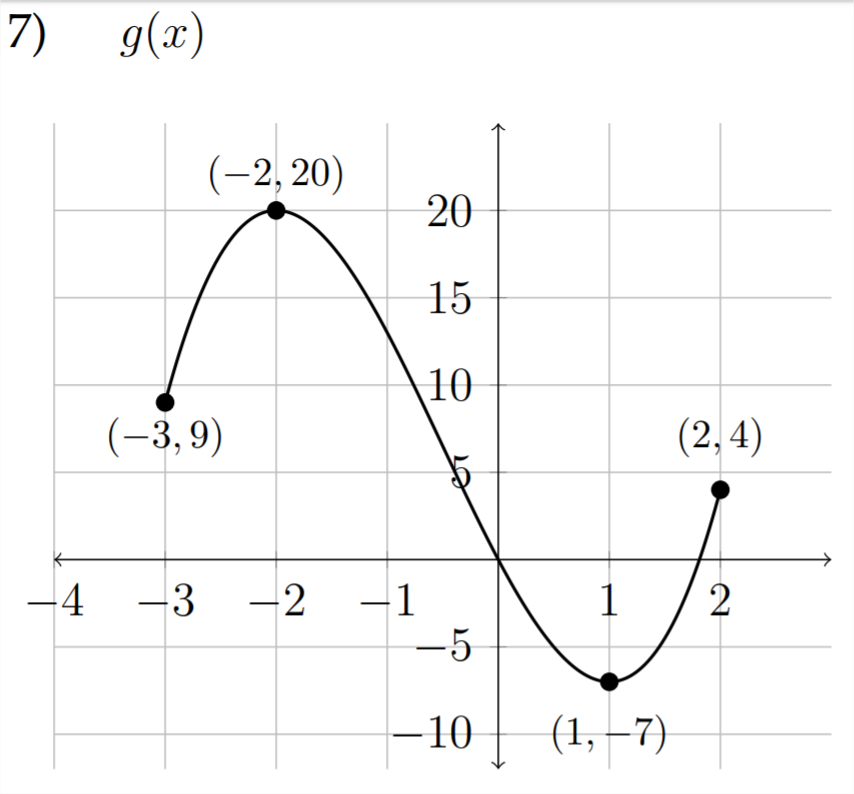
$clipboard_ef971dd6033506d049e078dd2bfd9ee88.png$
а)$\quad g(x-2)$
б$\quad-g(x)+1$
) в)$\quad 2 g(x-1)$
г)$\quad \frac{1}{2} g(x)-3$