4.9: Оптимізація

Last updated
Save as PDF

Page ID: 58777

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Одним з основних застосувань диференціального числення є оптимізація. Це процес знаходження максимальних або мінімальних значень функції для заданого співвідношення. Існує чотири типових типи проблем, які ми розглянемо в цьому розділі.
а) Аналітична оптимізація - ці завдання зазвичай використовують формулу відстані для визначення найближчої точки до певної кривої.

б) Геометрія/оптимізація витрат - ці проблеми, як правило, дають коробку або контейнер певної форми і просять або визначити найдешевшу вартість виготовлення з урахуванням конкретного обсягу або визначити найбільший обсяг з урахуванням конкретної вартості.

в) Оптимізація відстані - ці завдання зазвичай використовують два об'єкти, що рухаються під прямим кутом один до одного і визначають максимальну або мінімальну відстань між об'єктами.

г) Оптимізація відстань/витрат - ці проблеми зазвичай орієнтовані на ситуацію, в якій дві відстані під прямим кутом можна скоротити діагоналлю в певній точці, щоб мінімізувати витрати або час.

Аналітична оптимізація
\ [
d=\ sqrt {\ left (x_ {2} -x_ {1}\ праворуч) ^ {2} +\ left (y_ {2} -y_ {1}
\ справа) ^ {2}}\]
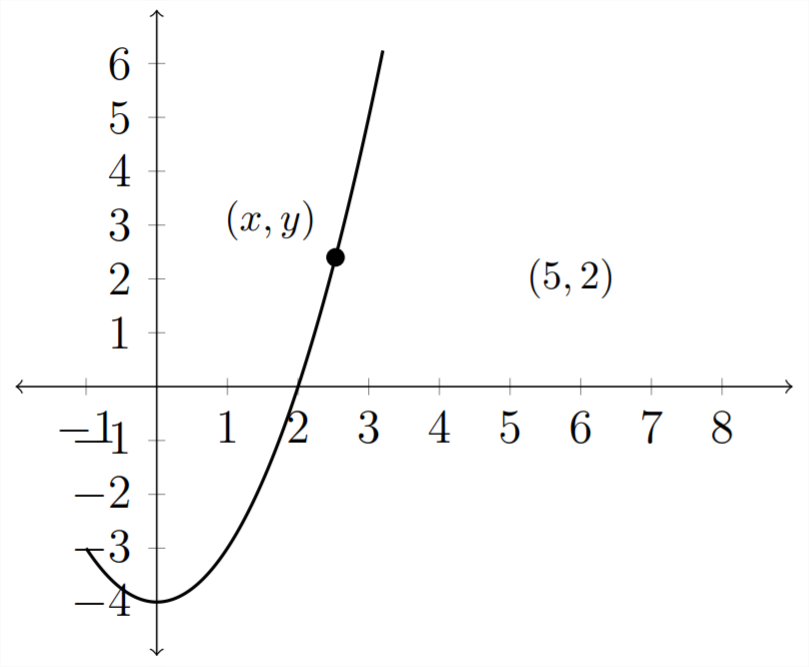
1) Висловлюємо відстань точки$(x, y)$ (в першому квадранті) на графі параболи$y=x^{2}-4$ від точка (5,2) як функція$x$
2) Використовуйте графік функції відстані$d(x)$ від частини I для визначення точки графіка параболи,$y=x^{2}-4$ яка найближча до точки (5,2)
3) Як далеко ця точка від точки (5,2)$?$
$clipboard_e77dd5a4742465589dcf46a0206809e77.png$
1) Використовуючи формулу відстані можна$d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}},$ сказати, що будь-яка точка на кривій$y=x^{2}-4$ - це відстань:
\ [
d=\ sqrt {(x-5) ^ {2} + (y-2) ^ {2}}
\]
від точки$(5,2) .$ Оскільки питання просить, щоб це було виражений як функція,$x,$ ми повинні замінити$y$ змінну на еквівалентний вираз за участю$x$
\ [
\ begin {масив} {c}
d=\ sqrt {(x-5) ^ {2} +\ left (x^ {2} -4-2\ справа) ^ {2}}\
\ text {or}\\
d=\ sqrt {(x-5 ) ^ {2} +\ ліворуч (x^ {2} -6\ праворуч) ^ {2}}
\ end {масив}
\]

2) Графік цієї функції відстані знаходиться нижче:
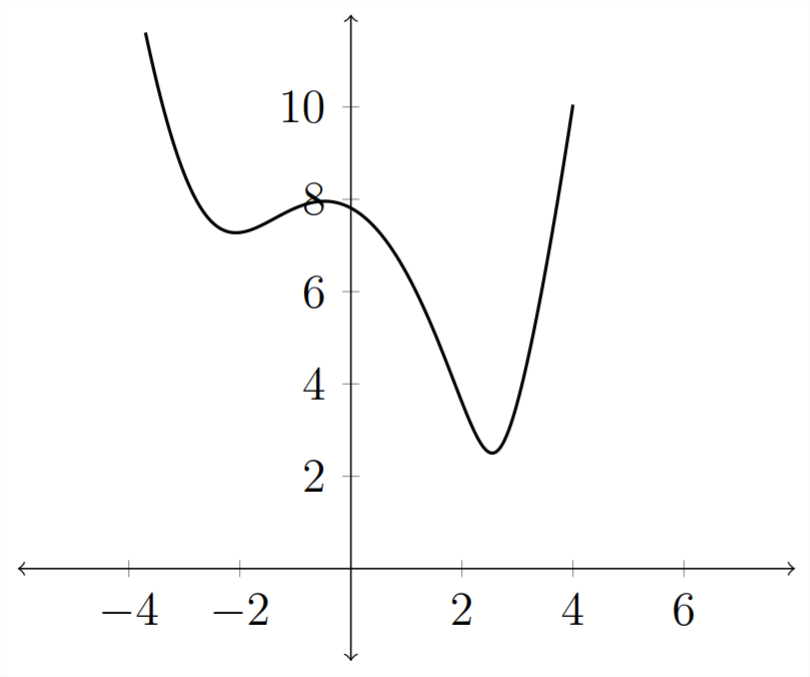
$clipboard_e3b603f080c13b1f6de005b109ebee647.png$
Зверніть увагу, що на цьому графіку$x$ вісь представляє$x$ значення з початкового графіка, але$y$ вісь на цьому графіку - це відстань точки на вихідній кривій від точки$(5,2) .$ Ми бачу, що ця функція відстані має чітке мінімальне значення, яке відбувається між$x=2$ і$x=4 .$ Ми можемо використовувати графічний калькулятор, щоб знайти це значення - в Обчислення ми б використали алгебру, щоб знайти це значення.
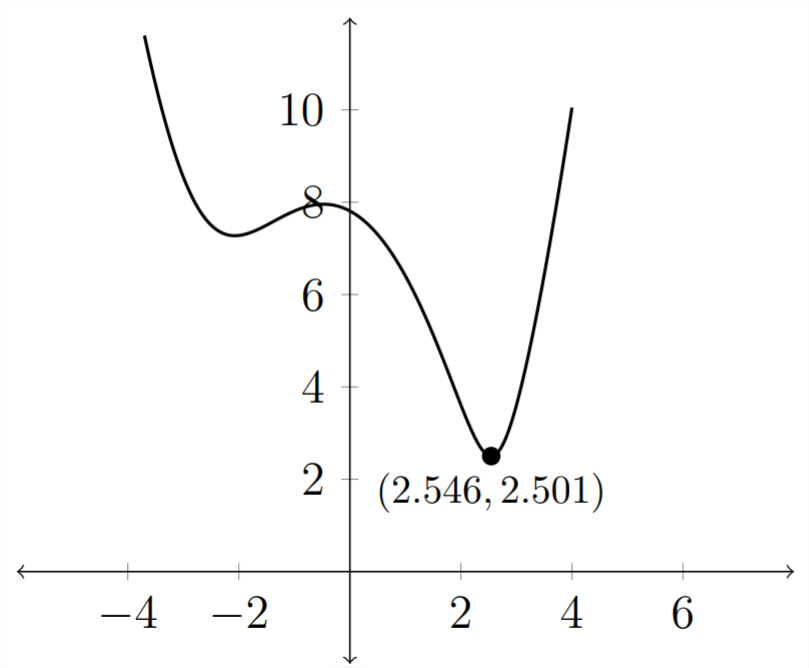
$clipboard_ed564b29313f15e8baf2048d0f743b1e1.png$
Обидва значення, зазначені в графіку, є приблизними. Значення$x \approx 2.546$ вказує на$x$ значення точки на вихідній кривій, яка найближча до точки (5,2).$y \approx 2.501$ Позначає відстань точки від точки (5,2),
оскільки$x$ значення точки на вихідній кривій, яка найближча до точки (5,2) приблизно це означає$2.546,$, що$y$ значення:
\ [
y=x^ {2} -4\ приблизно 2.546^ {2} -4\ приблизно 6.482-4\ приблизно 2.482
\]
Отже відповідь для частини 2 полягає в тому, що (2.546,2.482) є найближчою точкою на кривій$y=x^{2}-4$ до точки (5,2)
3) Ми вже визначили відстань, коли знайшли мінімальну точку на графіку відстані. Відстань становить близько 2,501 одиниць.

Вправи$4.9(a)$
1) З огляду на функцію$f(x)=4-x^{2}$, знайти$x$ і$y$ координати точки на кривій, яка найближча до точки$(7,3) .$ Як далеко від точки (7,3) знаходиться точка, яку ви знайшли?
2) З огляду на функцію$f(x)=6-x^{2},$ find$x$ і$y$ координати точки на кривій, яка найближча до точки$(1,1) .$ Як далеко від точки (1,1) знаходиться точка, яку ви знайшли?
3) З огляду на функцію$f(x)=x^{2}+2 x-5,$ find$x$ і$y$ координати точки
на кривій, яка найближча до точки$(-2,5) .$ Як далеко від точки (-2,5) знаходиться точка, яку ви знайшли?
4) З огляду на функцію$f(x)=x^{2}-5 x+8,$ find$x$ і$y$ координати точки на кривій, яка найближча до точки$(-2,2) .$ Як далеко від точки (-2,2) знаходиться точка, яку ви знайшли?
5) З огляду на функцію$f(x)=x^{3}-4 x^{2}+2 x+1,$ find$x$ і$y$ координати точки на кривій, яка найближча до точки$(2,1) .$ Як далеко від точки
(2,1) знаходиться точка, яку ви знайшли?
6) З огляду на функцію$f(x)=2 x^{3}-5 x-1,$ find$x$ і$y$ координати точки
на кривій, яка найближча до точки$(-2,8) .$ Як далеко від точки (-2,8) знаходиться точка, яку ви знайшли?
7) Прямокутник має один кут у 1-му квадранті на графіку$y=16-x^{2}$ одного кута біля початку та два інших кути на позитивній$x$ осі та позитивній$y$ осі.
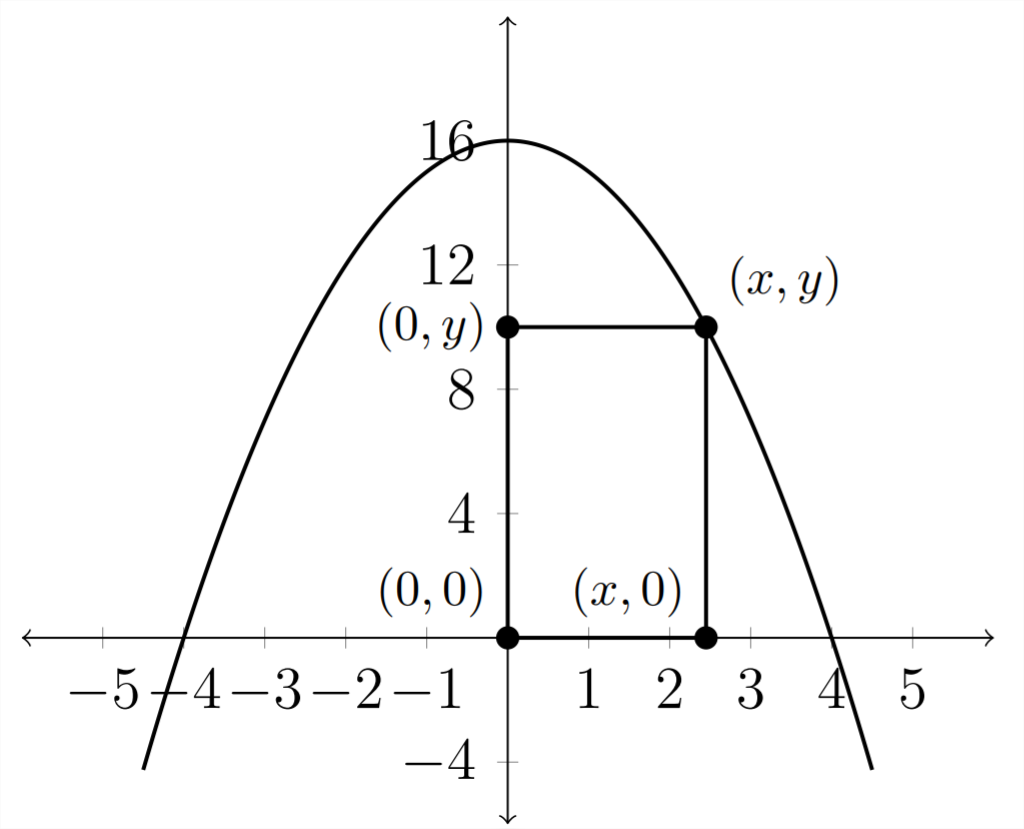
$clipboard_edd7efcab8fd1498b082c528ca5f3c240.png$
а) Висловіть$A$ площу прямокутника як функцію$x$.
б) Для якої$x$ величини площа найбільша?
в) Яка максимальна площа?

8) Прямокутник вписується в півколо радіусом 5 так, щоб два кути знаходилися на$x$ осі і два кути - на півколі.
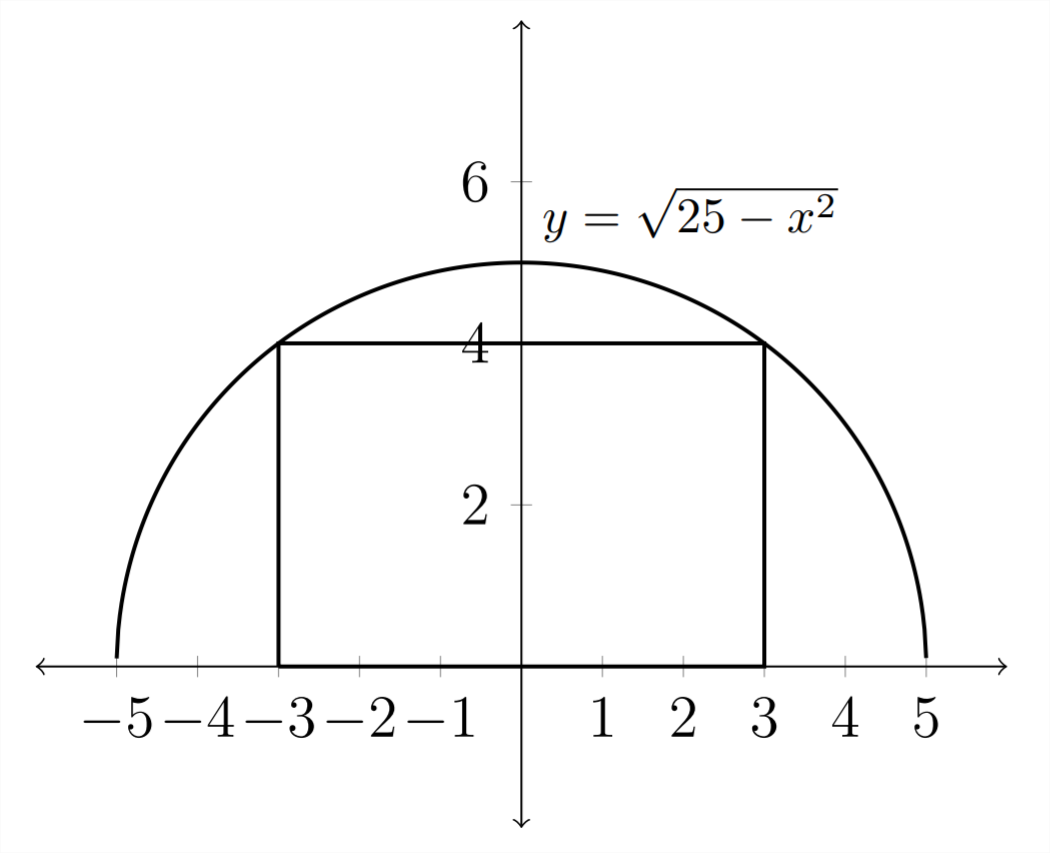
$clipboard_e652563c536276598174806a09ab77b0e.png$

Формула для графіка півкола -$y=\sqrt{25-x^{2}}$
а) Висловіть площу$A$ прямокутника як функцію$x$.
б) Для якої$x$ величини площа найбільша?
в) Яка максимальна площа?

Геометрія/оптимізація
витрат Закрита коробка з квадратною основою будується з матеріалу, який коштує$\$ 1$$\mathrm{ft}^{2}$ за чотири сторони та знизу та$\$ 5$$\mathrm{ft}^{2}$ за верхню. Які розміри коробки найбільшого обсягу, які можна спорудити для$\$ 72 ?$

Є два питання, з якими ми працюємо в цій задачі - обсяг коробки і площа поверхні коробки. Обсяг коробки важливий, тому що це те, що ми прагнемо максимізувати. Площа поверхні коробки важлива, тому що саме це буде контролювати вартість коробки - зверніть увагу, що витрати даються в перерахунку на$\mathrm{ft}^{2}$ квадратні фути, що пов'язано з площею поверхні.

Коробка має квадратну основу, але висота якогось іншого виміру -$h$. Так обсяг коробки буде довжиною$*$ шириною$*$ висотою, але так як коробка має квадратну основу, то довжина і ширина будуть однаковими - ми їх назвемо$x$. З цього ми бачимо, що обсяг можна виразити так:
\ [
v=x* x* h=x^ {2} h
\]
Для вартості коробки нам потрібно знати площу поверхні. Кожна сторона коробки повинна бути включена - основа і верх мають однакову площу ($x^{2}$), оскільки вони обидва квадрати, які є$x$ одиницями з кожного боку. Чотири сторони коробки - це всі прямокутники, які знаходяться$x$ за$h$ одиницями. Це означає, що кожен має площу$x * h-$ так всі чотири буде$4 * x * h$ або$4 x h$
Це робить площу поверхні коробки:
\ [
S=2 x^ {2} +4 x h
\]
Вартість коробки тоді буде:
\ [
C=x^ { 2} (\ $1) +x^ {2} (\ $5) +4 x h (\ $1)
\]
Тут ми бачимо, що один$x^{2}$ множиться на$\$ 1,$ тому, що нижня буде коштувати$\$ 1$ за,$\mathrm{ft}^{2},$ а інша$x^{2}$ множиться на$\$ 5,$ тому, що верхня вартість$\$ 5$ per$\mathrm{ft}^{2}$. Чотири сторони:$4 x h$ також множиться на\ $1.

Отже, наша остаточна формула вартості така:
\ [
C=6 x^ {2} +4 x h
\]
але ми вже знаємо, що хочемо витратитися$\$ 72$ на коробку, тому можна сказати, що:
\ [
72=6 x^ {2} +4 x h
\]
Це означає, що:
\ [
\ begin {масив} {c}
\ frac {72-6 x^ {2}} {4 x} =h\
\ text {or}\
\ frac {18} {x} -1.5 x=h
\ end {масив}
\]
Причина, чому це важливо, полягає в тому, що це дозволить нам висловити обсяг поле з точки зору$x .$ Пам'ятайте, що обсяг був:
\ [
v=x^ {2} h
\]
так що тепер ми можемо бачити, що:
\ [
\ begin {масив} {c}
v=x^ {2}\ left (\ frac {18} {x} -1.5 x\ праворуч)\
\ text {або}\\
V=18 x-1.5 x^ {3}
\ кінець {масив}
\]

Графік для цієї функції наведено нижче:

Ми бачимо на графіку, що максимальний обсяг, заданий вартістю,$\$ 72$ буде тоді, коли основа коробки становить 2 фути на 2 фути. Обсяг буде$24 \mathrm{ft}^{3}$ і висота складе 6 футів. Отже, відповідь на питання:$2 \mathrm{ft} \times 2 \mathrm{ft} \times 6 \mathrm{ft}$

Вправи$4.9$ (б)
1) Прямокутна ємність для зберігання з відкритим верхом має обсяг$10 \mathrm{m}^{3}$. Довжина його підстави в два рази більше ширини. Матеріал для підстави коштує$\$ 10$ квадратний метр. Борти вимагають матеріалу, який коштує$\$ 6$ квадратний метр. Знайдіть вартість матеріалів для найдешевшої такої тари.
2) Плакат повинен містити$108 \mathrm{cm}^{2}$ друковану продукцію, з полями$6 \mathrm{cm}$ кожного вгорі та внизу сторінки та з кожного$2 \mathrm{cm}$ боку сторінки. Яка мінімальна вартість плаката, якщо він буде виготовлений з матеріалу, який коштує$\$ 0.20$ квадратний сантиметр?
3) Якщо$1200 \mathrm{cm}^{2}$ з матеріалу є зробити коробку з квадратною основою і відкритим верхом, знайдіть максимально можливий обсяг коробки.
4)$\quad A$ коробка з квадратною основою і відкритим верхом повинна мати обсяг$32,000 \mathrm{cm}^{3}$ Знайти розміри коробки, що мінімізує кількість використовуваного матеріалу.
5) Нормандське вікно має форму півкола поверх прямокутника так, щоб діаметр півкола був таким же, як ширина прямокутника. З огляду на, що периметр вікна повинен бути$30 \mathrm{ft}$, знайдіть розміри вікна, які будуть пропускати найбільшу кількість сонячного світла (максимально збільшити площу).
6) Прямокутна коробка без верху повинна бути виготовлена з матеріалу вартістю$\$ 0.50$ квадратного фута. Ширина підстави становить 5 футів і вона буде мати обсяг$6 \mathrm{ft}^{3}$. Які розміри коробки мінімізують вартість? Яка вартість цього ящика?
Площа поверхні циліндра$=2 \pi r^{2}+2 \pi r h$
Обсяг циліндра$=\pi r^{2} h$
7) Циліндрична банка з верхом буде виготовлена з 200$^{2}$ дюймів олова. Якою була б висота і радіус банки максимального обсягу?
8) Циліндрична банка з верхом матиме обсяг$500 \mathrm{cm}^{3}$. Якщо сторони і нижня вартість$\$ 0.002$$\mathrm{cm}$ квадрата, а верхні витрати$\$ 0.0035$ на квадрат$\mathrm{cm},$ знайти розміри найменш дорогий банку, який буде мати обсяг$500 \mathrm{cm}^{3}$ Скільки коштує зробити цю банку?

Оптимізація відстані
Один корабель становить 10 миль на схід від буя і пливе на захід, до буя на 12 миль/год. Інший корабель знаходиться в 10 милі на південь від того ж буя і плавання через північ, також до буя на 7 миль/год.
а) Напишіть функцію, яка представляє відстань між двома кораблями з
$t,$ точки зору минулого часу в годинами.
б) Графік функції і визначення значення того,$t$ коли кораблі знаходяться найближче один до одного. Наскільки далеко один від одного знаходяться кораблі в цей час?
$t$Округлити значення до найближчого 100 го години.
Округлите відстань до найближчої десятої частки милі.
Ось діаграма, яка представляє проблему:
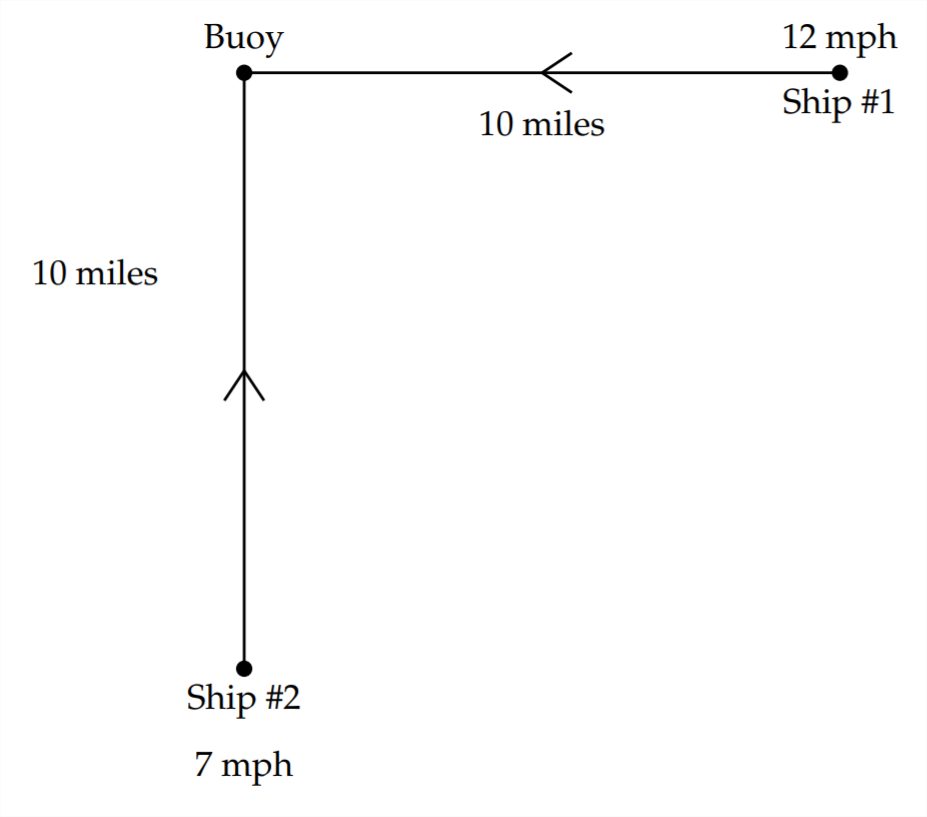
$clipboard_eb9e00c7329a1f1f445410b591e4a3238.png$
Відстань між двома кораблями вимірюється по діагоналі. Оскільки це створює прямокутний трикутник, ми можемо використовувати теорему Піфагора для представлення відстані між кораблями.
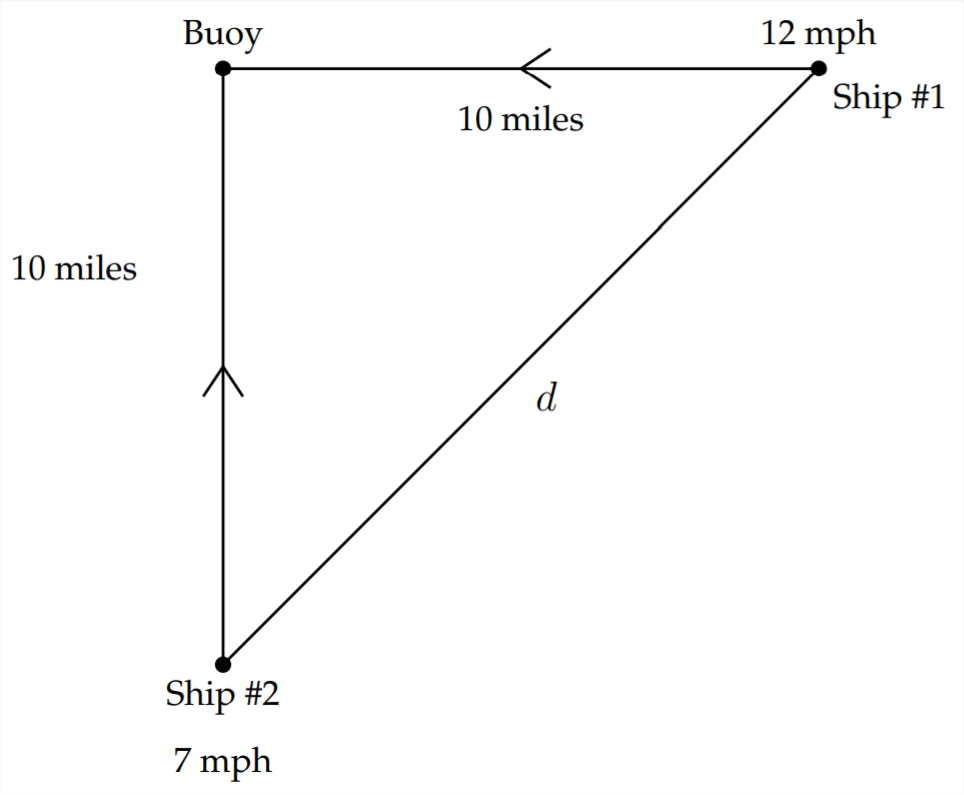
$clipboard_e74bee849393b3df7ec6a2df683b51955.png$

При цьому ноги прямокутного трикутника починаються як 10 миль, але вони стають коротшими, коли кораблі рухаються ближче до буя. Для корабля #1 відстань зменшується на 12 миль щогодини - це означає, що перший корабель пройде буй менш ніж за одну годину. Відстань між кораблем #1 і буєм можна представити як$(10-12 t)$ де$t$ знаходиться кількість годин, проведених у подорожі. Аналогічно відстань між кораблем #2 і буєм можна представити як$(10-7 t)$

Отже, використовуючи теорему Піфагора, ми можемо уявити відстань між кораблями в будь-який момент часу як:
\ [
d^ {2} =( 10-7 t) ^ {2} + (10-12 t) ^ {2}
\]
або
\ [
d=\ sqrt {(10-7 t) ^ {2} + (10-12 t) ^ {2}}
\]

Графік цієї функції відстані виглядає так:
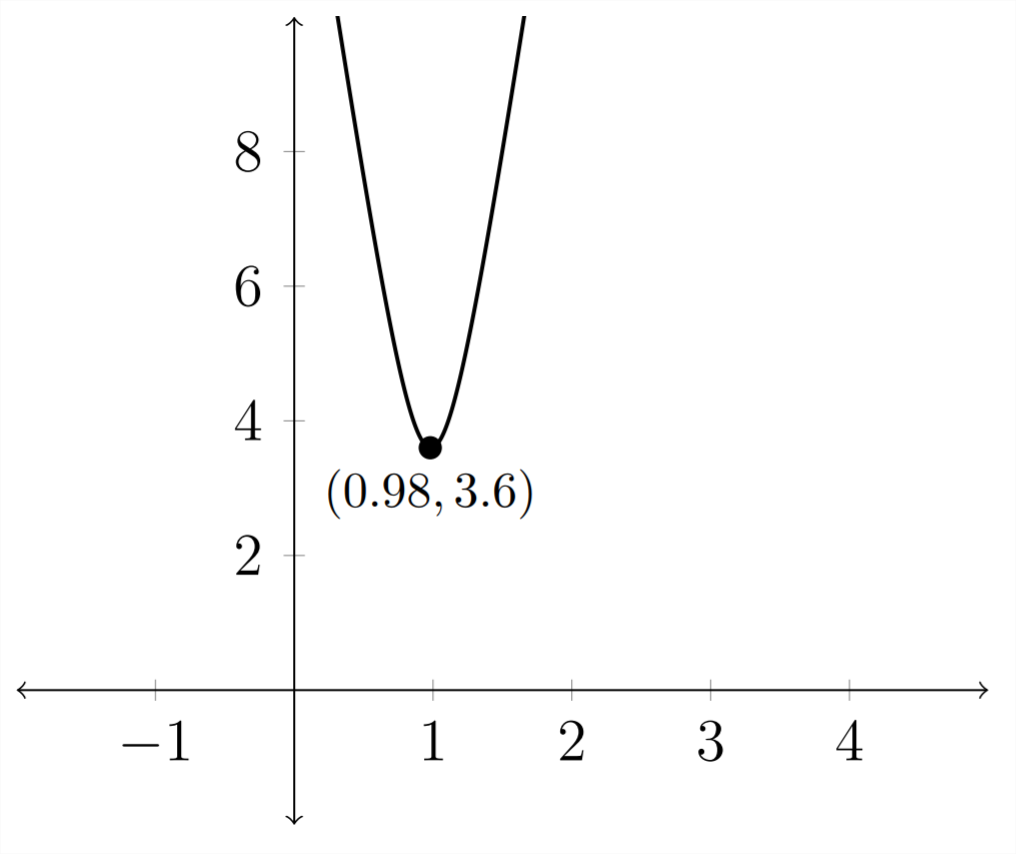
$clipboard_eb88a12d9da8ec2238680e51797cd86e5.png$
мінімальна точка на графіку відстані вказує час, в який кораблі знаходяться найближче один до одного. Після подорожі протягом 0,98 години кораблі будуть знаходитися на відстані приблизно 3,6 милі один від одного. Потім вони почнуть рухатися далі один від одного.

Вправи$4.9(c)$
1) Бігун починає бігати на північ від заданої точки, бігаючи зі швидкістю 5 метрів в секунду. При цьому другий бігун прямує на схід від тієї ж відправної точки, бігаючи зі швидкістю 8 метрів в секунду. Уявляють відстань між бігунами в залежності від часу$t,$, що минув. Скільки часу буде потрібно, щоб бігуни були на відстані 150 метрів один від одного?

2) Бігун починає бігати на північ від заданої точки, бігаючи зі швидкістю 10 метрів в секунду. При цьому другий бігун прямує на схід від тієї ж відправної точки, бігаючи зі швидкістю 7 метрів в секунду. Уявляють відстань між бігунами в залежності від часу$t,$, що минув. Скільки часу буде потрібно, щоб бігуни були на відстані 200 метрів один від одного?

3) На$1 \mathrm{pm}$ велосипеді 9 миль на північ від магазину морозива і їде на південь (до магазину морозива) на 15 миль/год. У той же час інший велосипедист знаходиться в 2 милі на схід від магазину морозива і їде на схід (подалі від магазину морозива) зі швидкістю 12 миль/год. Уявляють відстань між велосипедистів в будь-який момент часу після$1 \mathrm{pm}$. В який час відстань між гонщиками мінімальна? Наскільки вони знаходяться один від одного в цей момент?

4) Автомобіль залишає чотиристоронній перехрестя о 9:15 ранку, їде на південь зі швидкістю 70 миль/год. У той же час інший автомобіль знаходиться в 65 милі на захід від перехрестя, що їде на схід зі швидкістю 55 миль/год. Висловіть відстань між двома автомобілями як функцію часу, відколи вони покинули перехрестя. О котрій годині найближчі автомобілі? Наскільки далеко один від одного вони знаходяться в цей час?

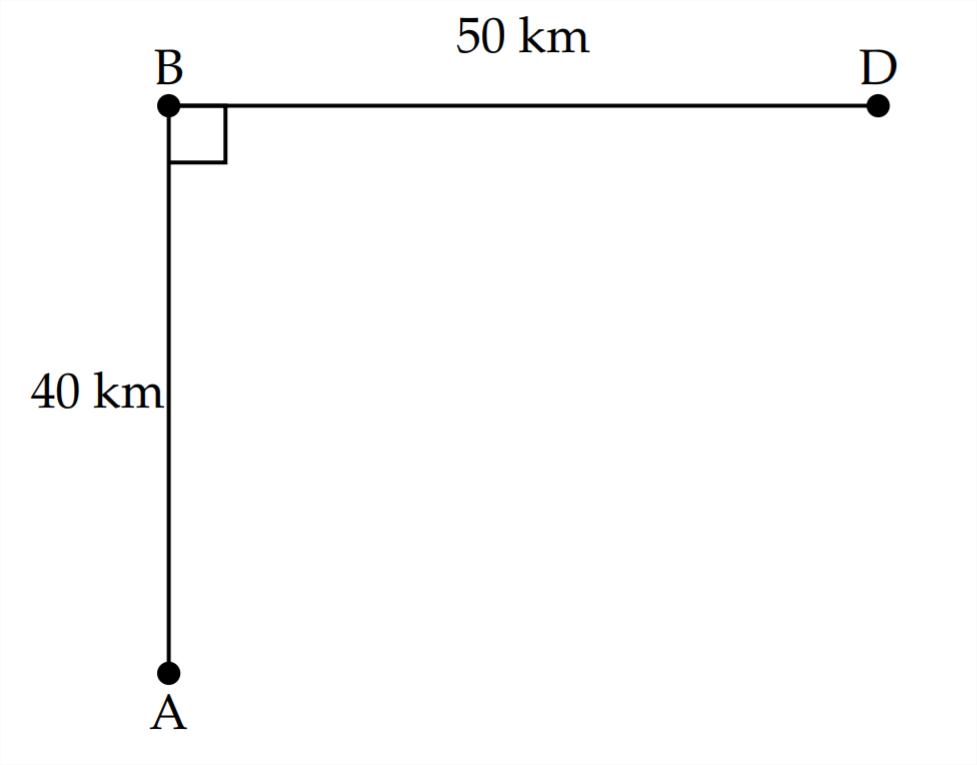
Опівдні дюна баггі знаходиться в пустелі в точці,$A$ зазначеній нижче. Точка$A$ йде$40 \mathrm{km}$ від асфальтованої дороги, яка охоплює$50 \mathrm{km}$ між точками$\mathrm{B}$ і$\mathrm{D}$

Якщо дюна баггі може проїхати 45 км/год в пустелі і 75 км/год на дорозі, де найкраще місце для того, щоб водієві покинути пустелю і повернути на дорогу, щоб мінімізувати час у дорозі?

О котрій годині водій прибуває до пункту,$D$ припускаючи, що він слідує шляхом протягом мінімального часу в дорозі?
$clipboard_e68c08dcf1e02297969accf18f1362a8d.png$
Один з варіантів полягає в тому, що дюна баггі може подорожувати по прямій лінії від А до Б (при 45 км/год), а потім подорожувати по асфальтованій дорозі від$\mathrm{B}$ до$\mathrm{D}$ (в$75 \mathrm{kph}$). Це займе$1.5 \mathrm{hrs}$
Інший варіант - баггі дюни подорожувати прямо від А до D на 45 км/год. Відстань тут приблизно$64 \mathrm{km}$ (знайдено за допомогою теореми Піфагора). Це означає, що час у дорозі становитиме близько 1.423 годин.

Оптимізація тут говорить про те, що, якби дюни баггі повинні були проїхати частину шляху в пустелі (по діагоналі) і решту шляху по асфальтованій дорозі, то може бути мінімальний час, який коротше, ніж 1.423 години. це займе йти прямо від$\mathrm{A}$ до$\mathrm{D}$
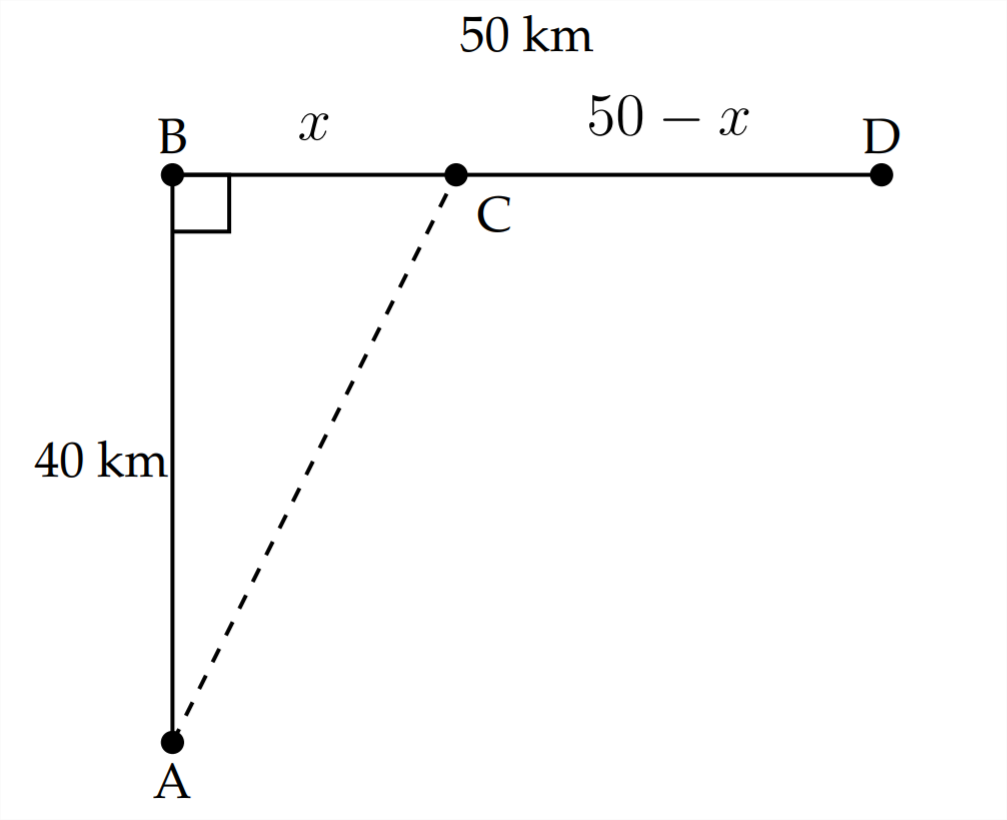
$clipboard_e2295318b695f61ac8d9ab88bb2320a63.png$
Якщо ми виражаємо відстань між$\mathrm{B}$ і$\mathrm{C}$ як$x,$ тоді відстань між$\mathrm{C}$ і D буде$50-x$. Відстань, пройдена в пустелі, - це відстань від А до,$C$ і це можна знайти за допомогою теореми Піфагора.
\ [
\ overline {A C} =\ sqrt {40^ {2} +x^ {2}} =\ sqrt {x^ {2} +1600}
\]
з тих$d=r * t,$ пір час, який потрібно проїхати задану відстань, буде$\frac{d}{r}=t$
У випадку цієї проблеми час для подорожі від А до С:
\ [
t_ {1} =\ frac {\ sqrt {x^ {2} +1600}} {45}
\]
Час подорожі$C$ до$D$:
\ [
t_ {2} =\ frac {50-x} {75}
\]
Отже, загальний час у дорозі буде:
\ [
t=t_ {1} + t_ {2} =\ розрив {x^ {2} +1600} {45} +\ гідророзриву {50-х} {75}
\]

Графік цієї функції знаходиться нижче:
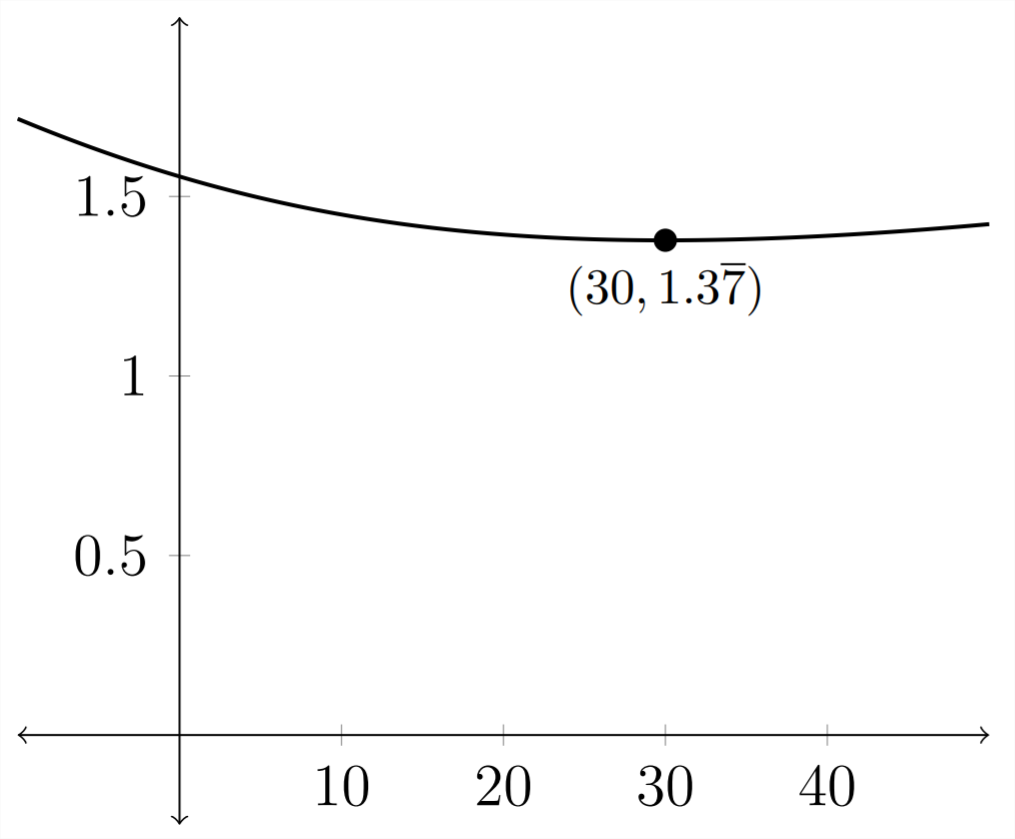
$clipboard_e2412b12667e8bcb0ec65a5eda119bfbd.png$
Важко побачити, але є мінімум для графіка де$x=30$ і$t=1.3 \overline{7}$

Вправи$4.9(d)$
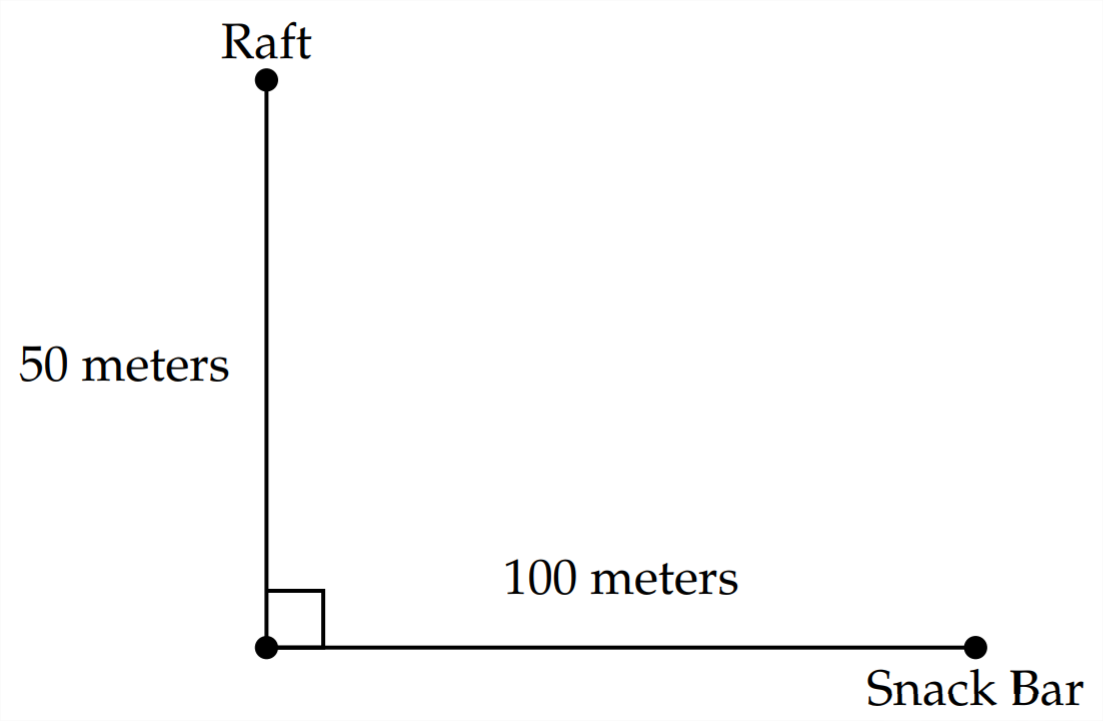
1) Жінка хоче доплисти до берега з плоту, який знаходиться в 50 метрах від берега, а потім бігти до закусочної, розташованої на 100 метрах вниз по береговій лінії. Жінка плаває 1 метр в секунду і бігає зі швидкістю 5 метрів в секунду. Де на береговій лінії вона повинна плавати, щоб мінімізувати час у дорозі?
$clipboard_ebe8f9a73ae39955568b3ebb25b6ab7ee.png$
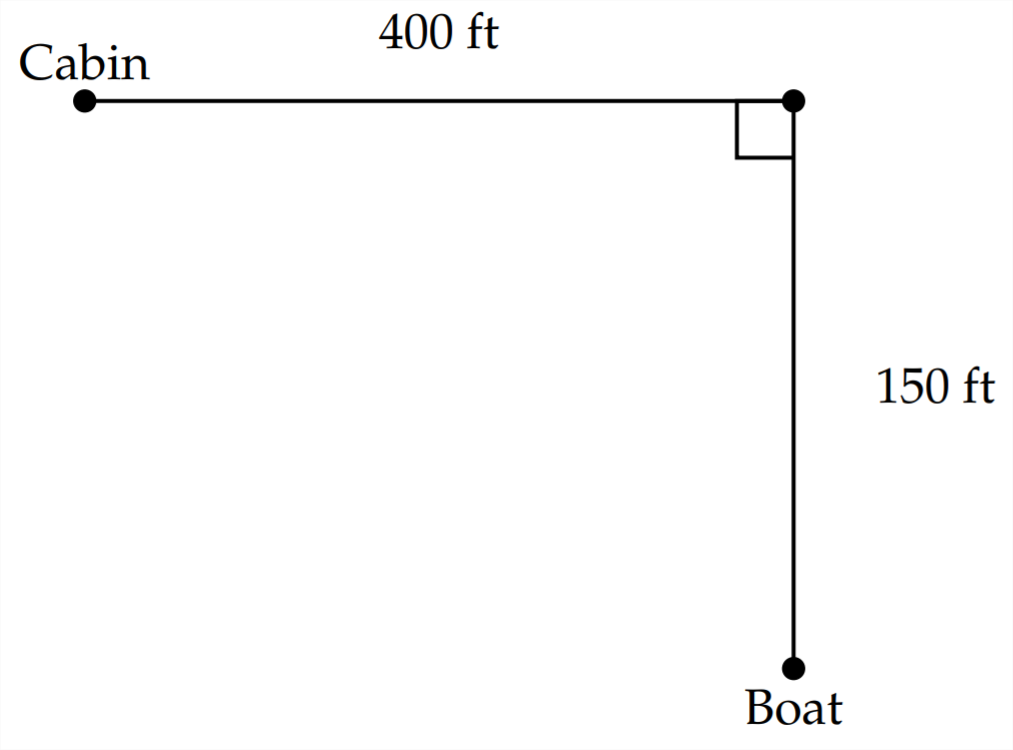
2) Чоловік знаходиться в човні на озері$150 \mathrm{ft}$ з берега. Він хоче повернутися в свою каюту. Він$400 \mathrm{ft}$ спускається по береговій лінії від салону. Він планує грести до берега, залишити човен, де він приземляється, а потім пробігти решту шляху до кабіни. Якщо він рядки 7 футів в секунду і працює 15 футів в секунду, де він повинен пляж човна, щоб мінімізувати час у дорозі?
$clipboard_e757f167e6800177b3679c37301149d65.png$
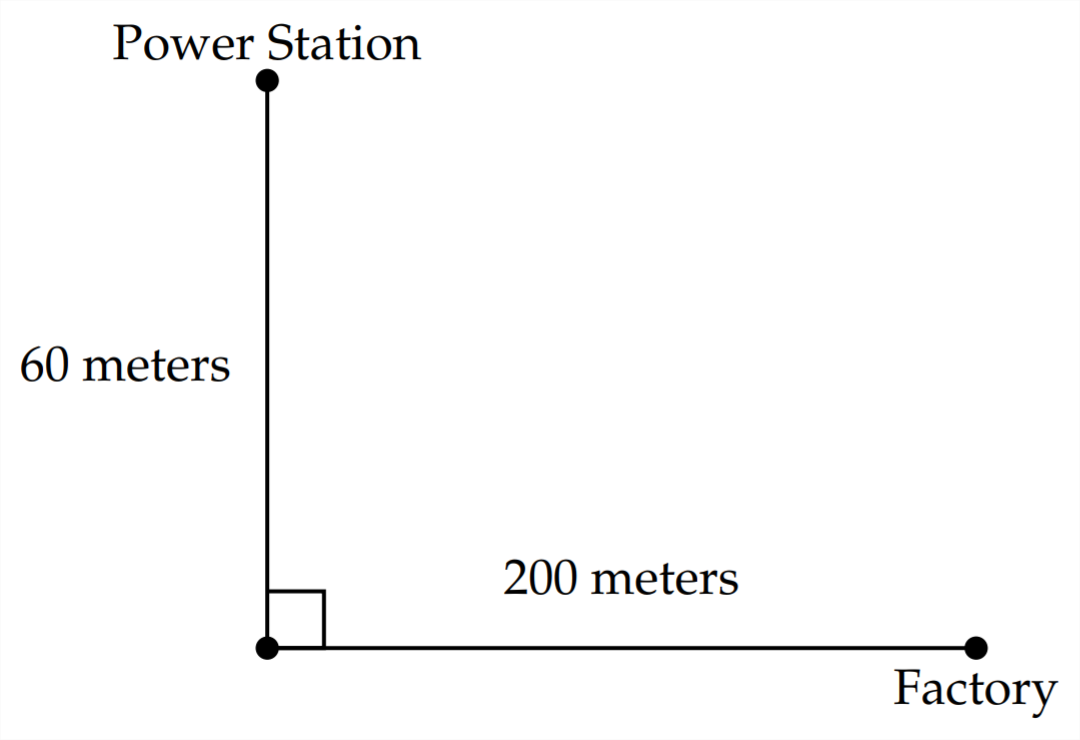
3) Електростанція і завод розташовані з протилежних боків річки шириною
60 метрів. Завод знаходиться в 200 метрах від точки на березі прямо навпроти електростанції. Між електростанцією і заводом повинна бути прокладена лінія електропередач. Це коштує$\$ 25$ за метр, щоб прокласти кабель в річці і$\$ 20$ за метр, щоб прокласти кабель на землі. Скільки кабелю потрібно прокласти в річці і скільки потрібно прокласти на суші, щоб мінімізувати витрати? Куди повинен виходити кабель на берег? Яка мінімальна вартість?
$clipboard_eaaccebcfb6fc58fd516de178e73e5110.png$
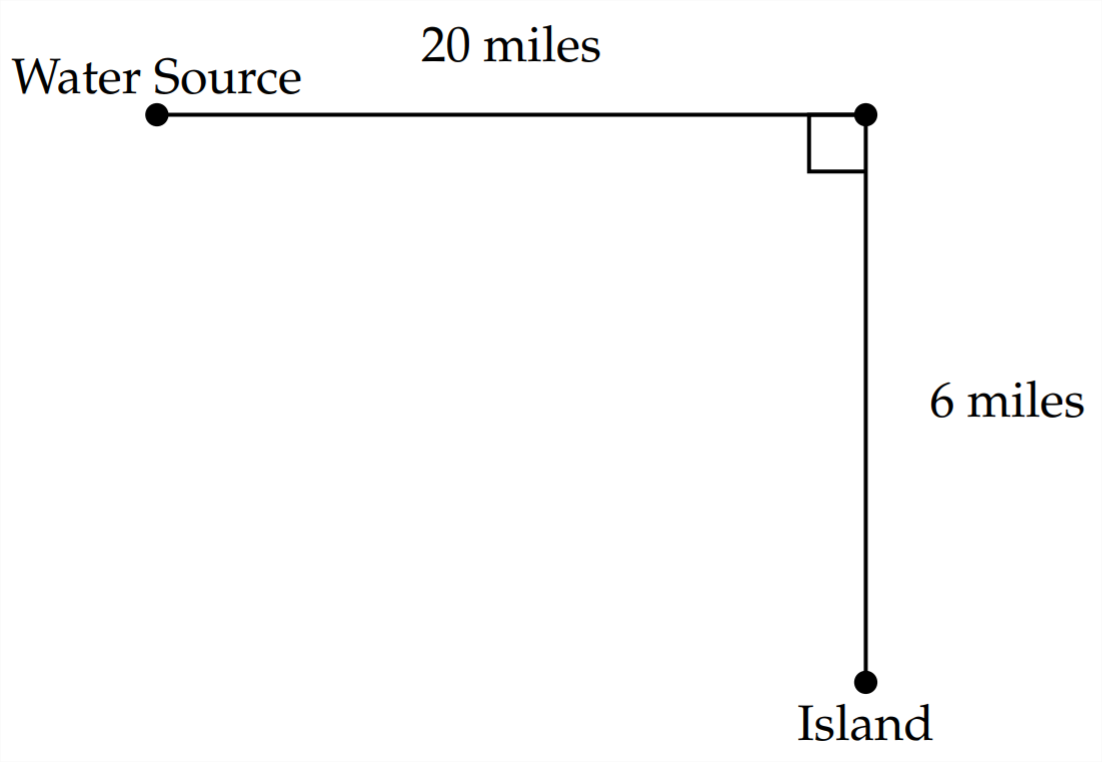
4) Прісноводний трубопровід будується до острова, який знаходиться в 6 милі від материка. Джерело води знаходиться на 20 милі вниз по узбережжю від точки на березі, яка знаходиться найближче до острова. Вартість прокладки трубопроводу уздовж берега -$\$ 8,000$ за милю, в той час як вартість прокладки трубопроводу в воді -$\$ 12,000$ за милю. Скільки повинен бути прокладений трубопровід у воді і скільки потрібно прокласти на суші, щоб мінімізувати витрати? Куди повинен виходити трубопровід від берега? Яка мінімальна вартість?
$clipboard_e29d8f6003738a82bac68edfa3b657840.png$