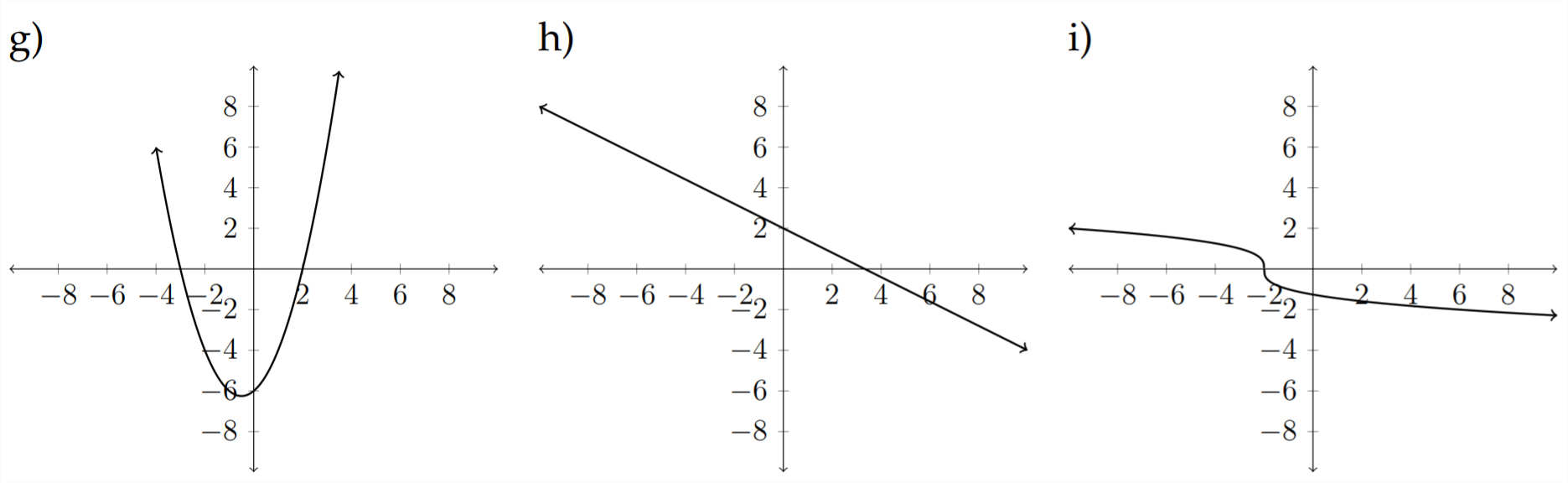4.5: Функції панелі інструментів

Last updated
Save as PDF

Page ID: 58809

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Вивчення загальних форм деяких загальних сімейств функцій може бути корисним при аналізі різних проблем. Це також може бути корисним у застосуванні ідей статистичної регресії. Статистична регресія зазвичай збирає набір точок даних і намагається пристосувати математичну функцію до точок даних. Вибір типу функції, яка буде найкращим чином відповідати даними, є важливим кроком у визначенні відповідної функції регресії.
Нижче наведено приклад лінійної регресії:
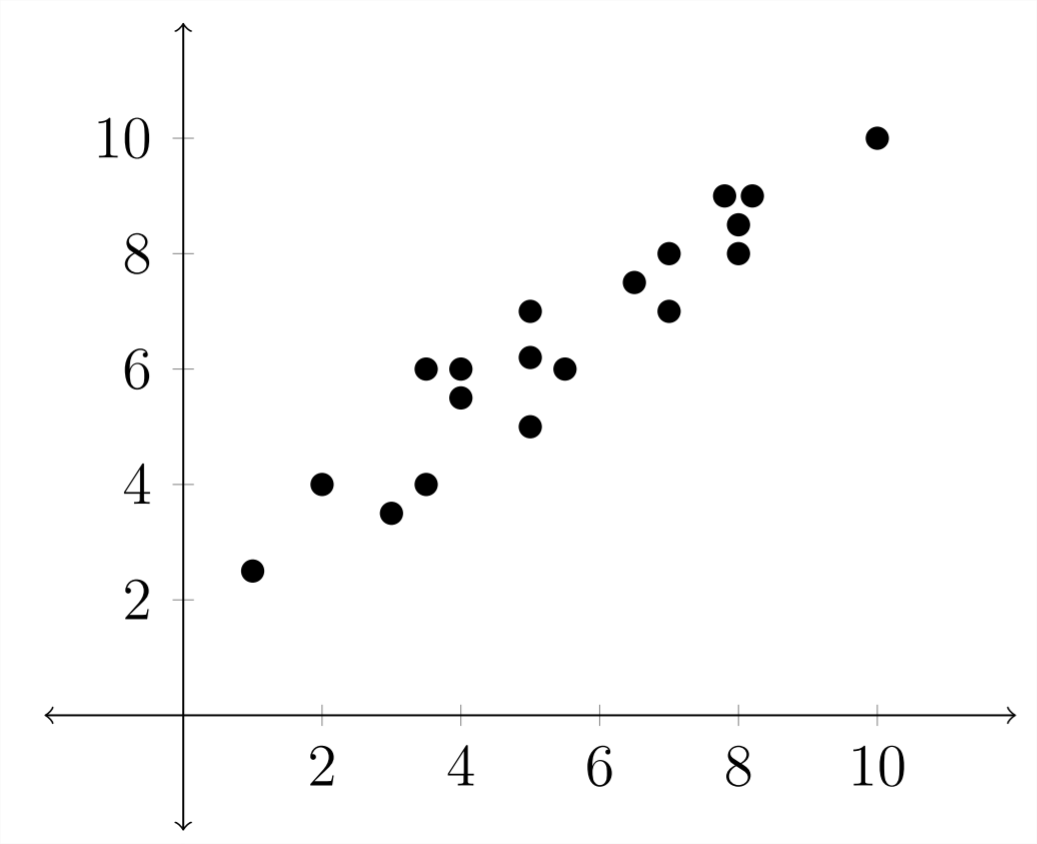
$clipboard_e92ff6e6b06d77f752cea4d3b716dd375.png$
На графіку нижче наведено приклад квадратичної регресії:
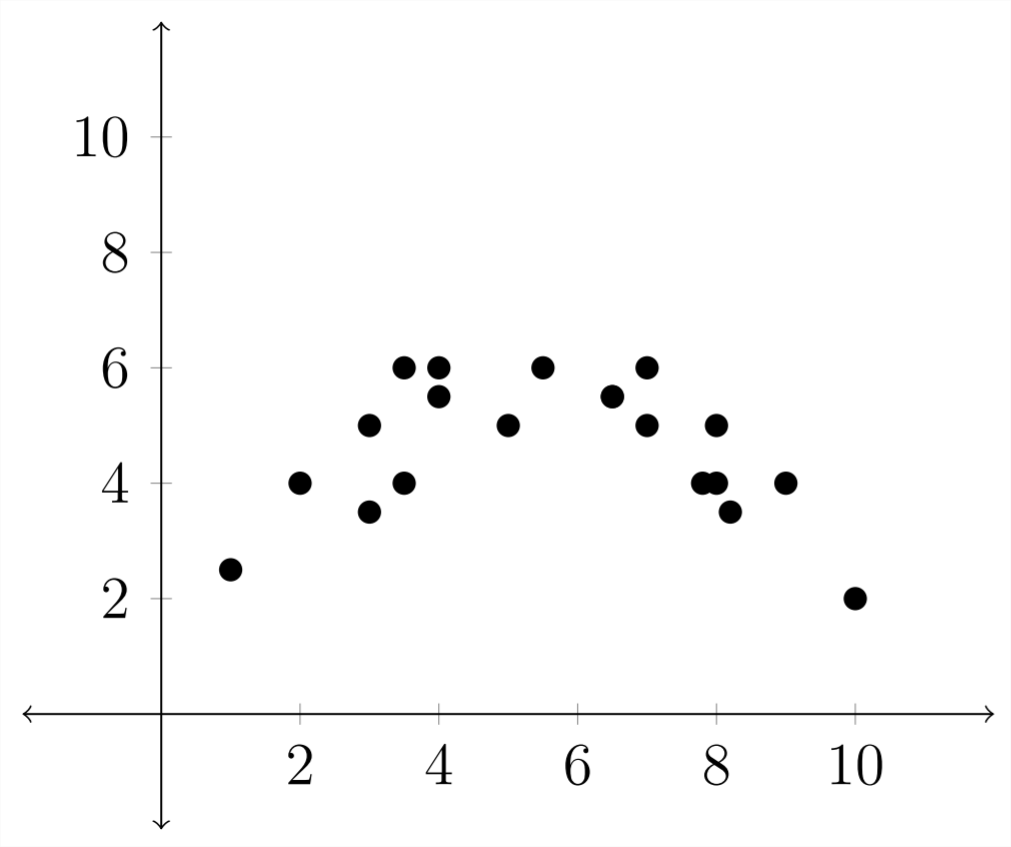
$clipboard_e4f6219ae160cd2347a566efc4cfc13b1.png$

Знайомство з типовою формою різних сімейств функцій може допомогти в аналізі експериментальних даних.
Стандартні сімейства функцій:
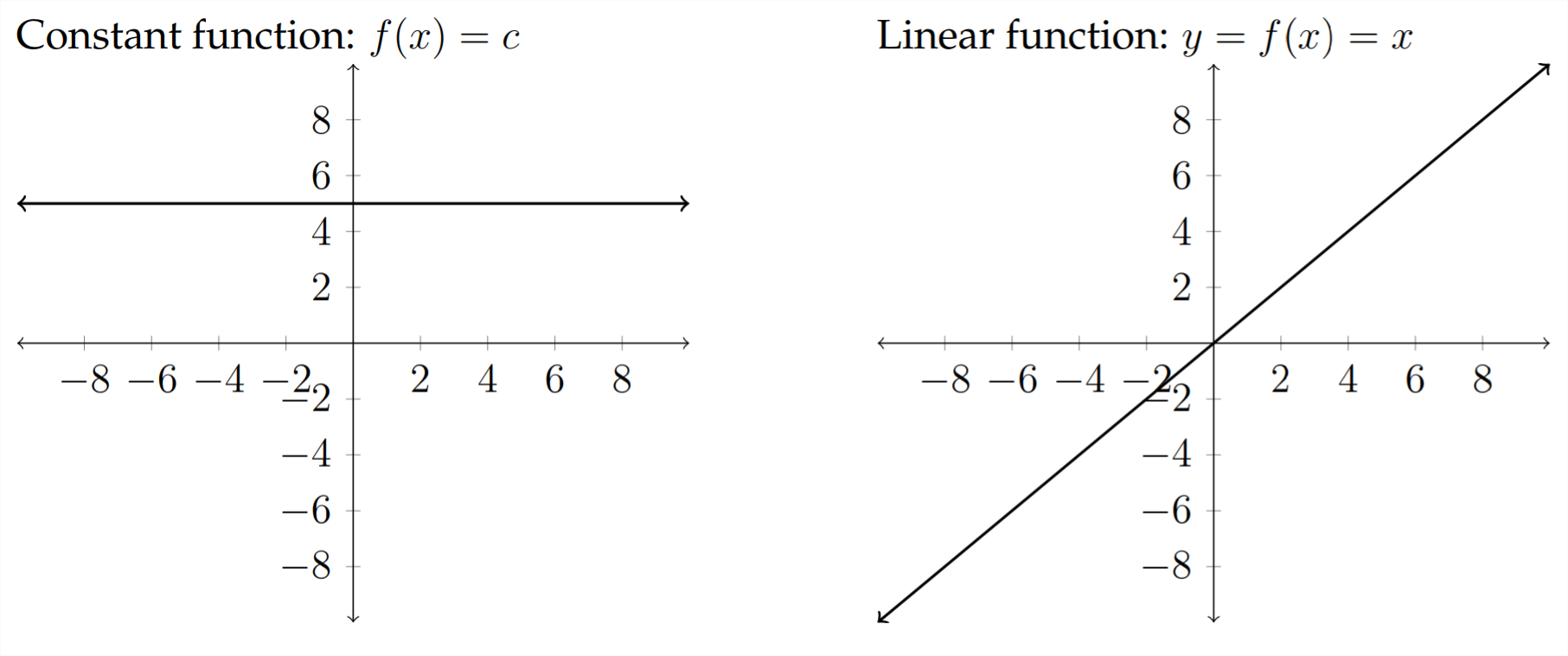
$clipboard_e84379dc841d116c1c9f1d82e057efbb4.png$
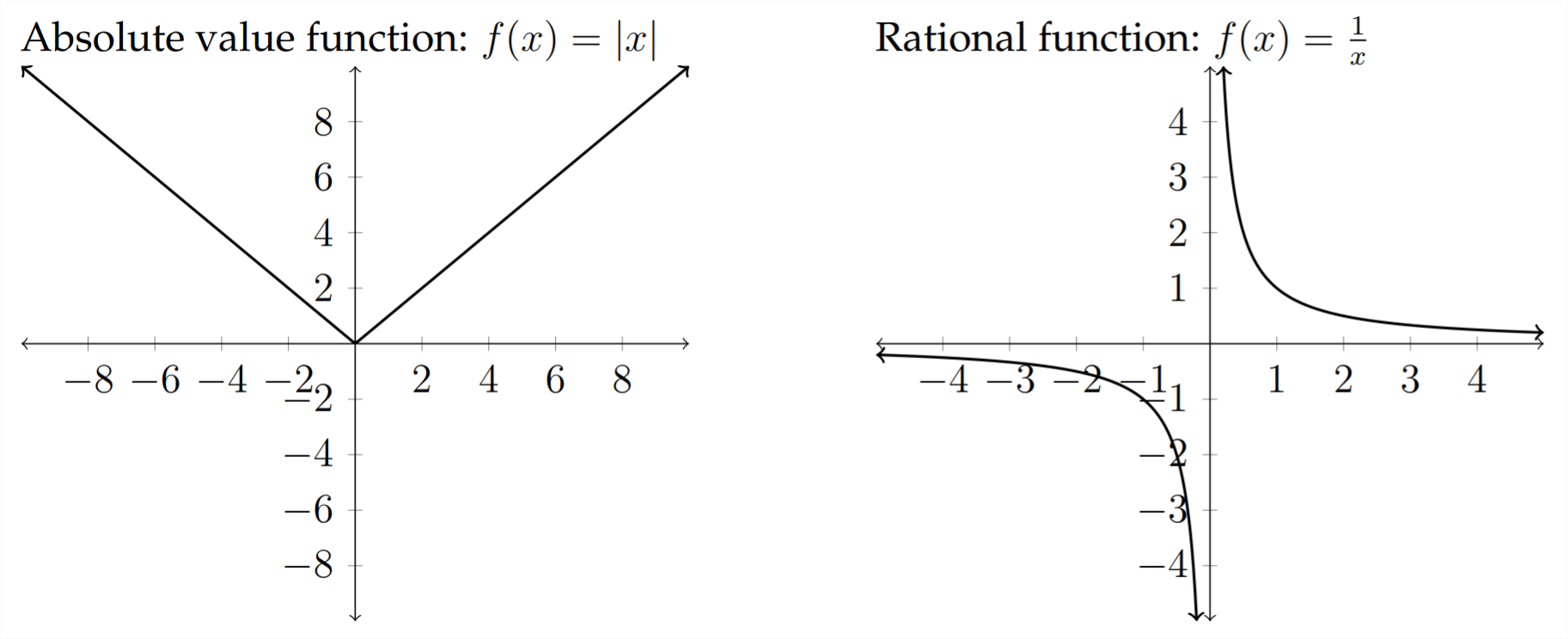
$clipboard_e9cfb271385bef3b95d4db2936d3a473c.png$
$clipboard_e4f837eba4dab5cbd4c18a3afc0cc4306.png$
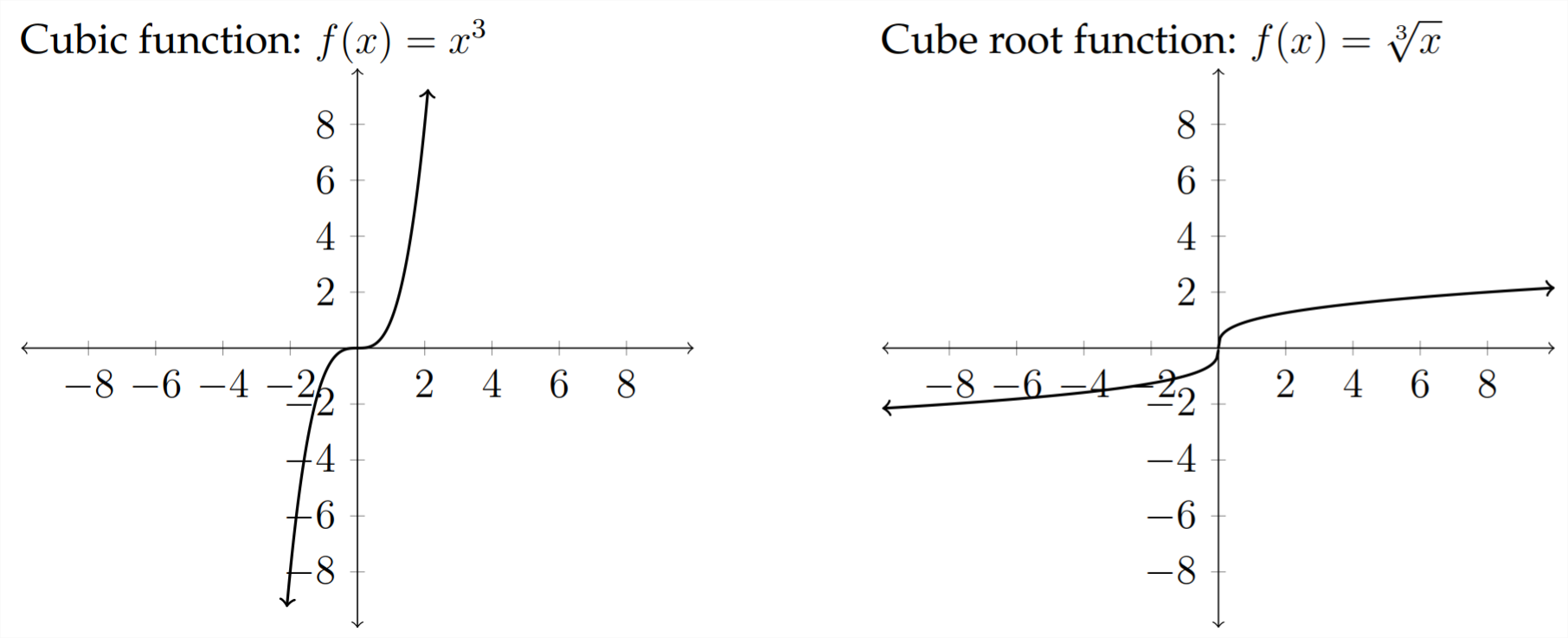
$clipboard_ea718e96f0f59b42c3494bafd4ad9ad51.png$
Деякі інші сімейства функцій, які ми не будемо обговорювати:

Експоненціальна функція:$\quad f(x)=a^{x}$
Логарифмічна функція:$f(x)=\log _{b} x$
Тригонометрична функція:$\quad f(x)=\sin x$

Вправи
4.5 Намалюйте графік для кожного з наступних перетворень.
1)$\quad f(x)=x^{2}+3$
2)$\quad f(x)=x^{2}-4$
3)$\quad f(x)=(x-5)^{2}+3$
4)$\quad f(x)=(x+1)^{2}-4$
5)$\quad f(x)=|x|-2$
6)$\quad f(x)=|x|+5$
7)$\quad f(x)=|x+3|-2$
8)$\quad f(x)=|x-1|+5$

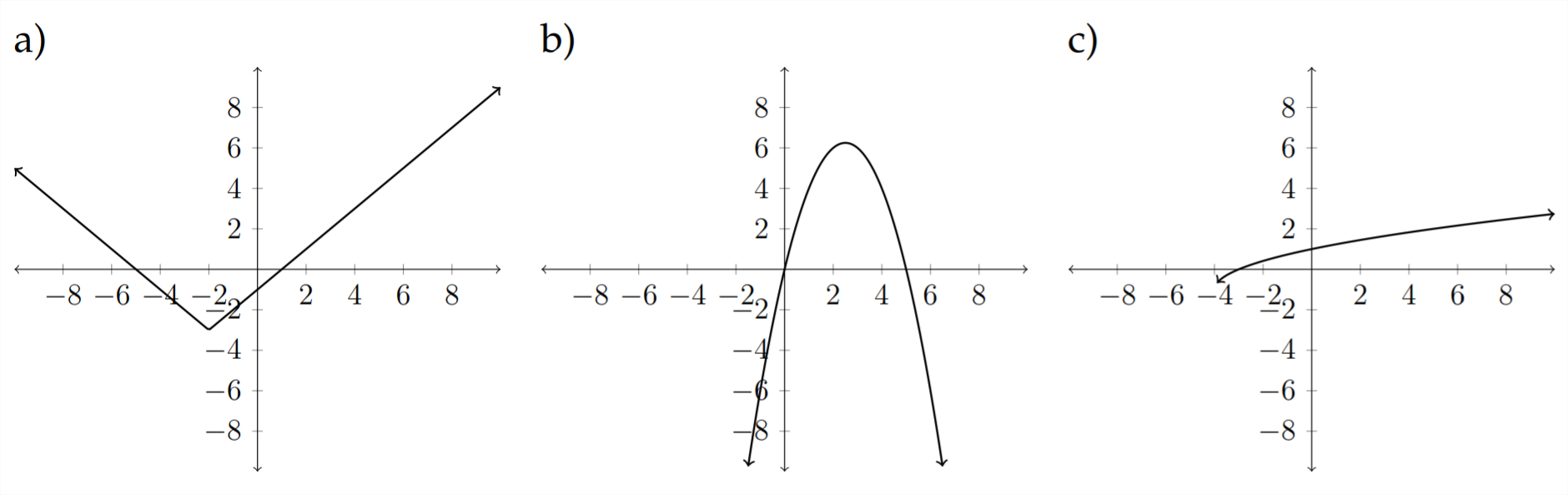
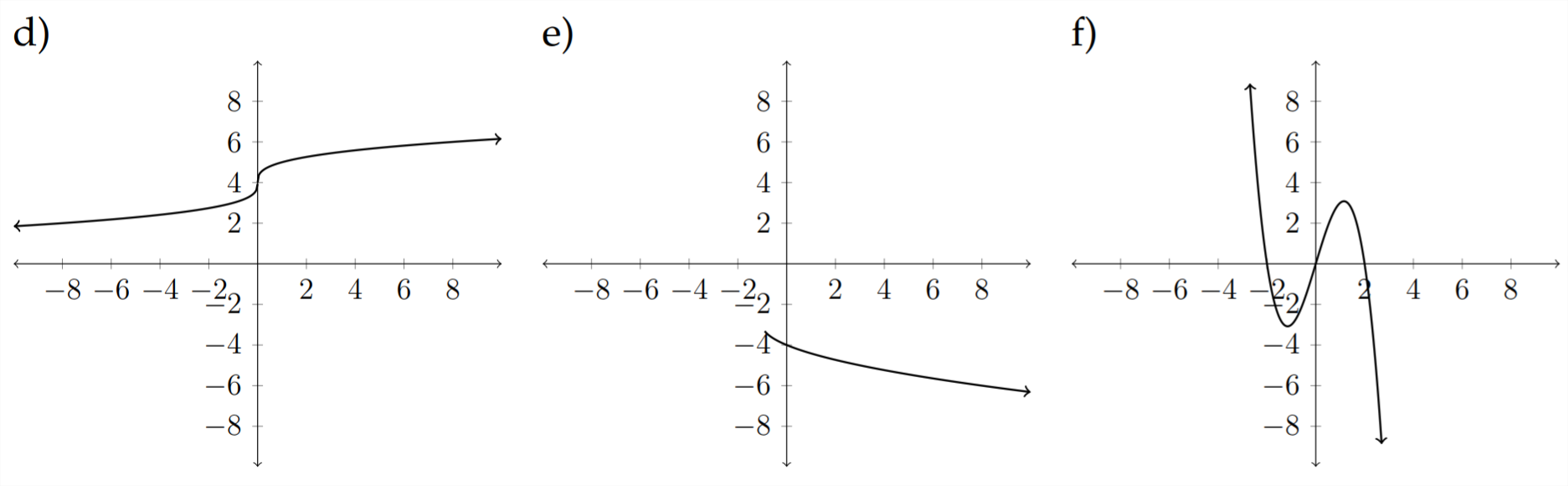
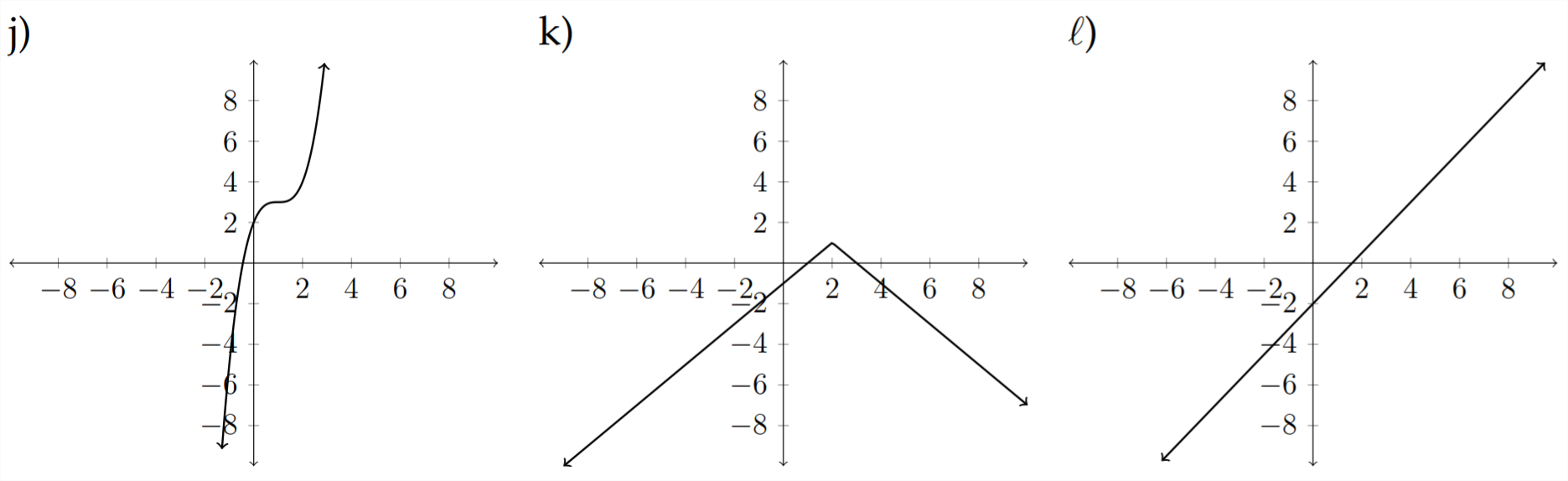
Зіставте кожне з наступних рівнянь з відповідним графіком.
9)$\quad f(x)=\sqrt{x+4}-1$
10)$\quad h(x)=x^{2}+x-6$
11)$\quad g(x)=|x+2|-3$
12)$\quad f(x)=4 x-x^{2}$
13)$\quad h(x)=-|x-2|+1$
14)$\quad g(x)=-\frac{3}{5} x+2$
15)$\quad h(x)=\sqrt[3]{x}+4$
16)$\quad f(x)=x^{3}-3 x^{2}+3 x+2$
17)$\quad g(x)=-\sqrt[3]{x+2}$
18) $\quad h(x)=-\sqrt{x+1}-3$
19)$\quad f(x)=\frac{5}{4} x-2$
20)$\quad f(x)=4 x-x^{3}$

$clipboard_ebb9a62b8c5ed71f527afa0ba943e368c.png$
$clipboard_e2c6bb433a9fb93a07d6f2847c770689f.png$
$clipboard_ef3516abb96cf1a28ed03ed79c6794546.png$
$clipboard_ef1af4e0402bd2bc31fe0863b5ea51ec5.png$