3.3: Домен і діапазон

Last updated
Save as PDF

Page ID: 59640

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Знайти область функції, визначеної рівнянням.
Графік кусково визначених функцій.

Якщо ви перебуваєте в настрої для страшного фільму, ви можете перевірити один з п'яти найпопулярніших фільмів жахів усіх часів - я Легенда, Ганнібал, Кільце, Недобра, і Закляття. Малюнок$\PageIndex{1}$ показує суму, в доларах, кожен з цих фільмів, гросових, коли вони були випущені, а також продажу квитків на фільми жахів в цілому по роках. Зверніть увагу, що ми можемо використовувати дані для створення функції суми кожного заробленого фільму або загального продажу квитків на всі фільми жахів по роках. Створюючи різні функції за допомогою даних, ми можемо ідентифікувати різні незалежні та залежні змінні, а також аналізувати дані та функції для визначення домену та діапазону. У цьому розділі ми розглянемо методи визначення області та діапазону функцій, таких як ці.

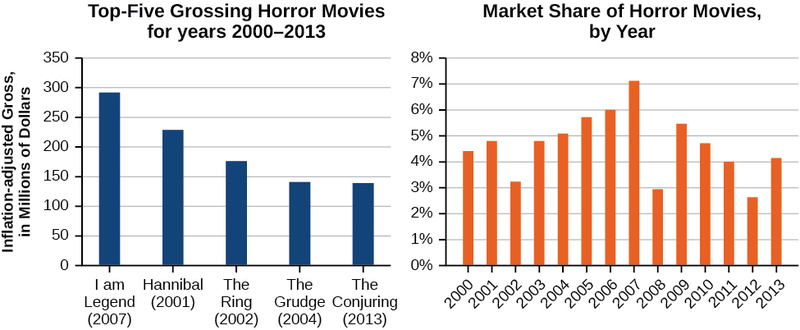
[Два графіка, де перший графік - п'ятірка касових фільмів жахів за роки 2000-2003 років та частка ринку фільмів жахів за роками — Малюнок$\PageIndex{1}$: Графік п'яти найкращих фільмів жахів за роки 2000-2003 років та графік частки ринку фільмів жахів за роками. На основі даних, зібраних www.the-numbers.com.

Пошук області функції, визначеної рівнянням

У Functions and Function Notation ми познайомилися з поняттями області та діапазону. У цьому розділі ми будемо практикувати визначення доменів і діапазонів для конкретних функцій. Майте на увазі, що при визначенні доменів та діапазонів нам потрібно враховувати, що фізично можливо або значуще в реальних прикладах, таких як продаж квитків та рік у прикладі фільму жахів вище. Потрібно також розглянути те, що математично дозволено. Наприклад, ми не можемо включити будь-яке вхідне значення, яке змушує нас взяти парний корінь від'ємного числа, якщо домен і діапазон складаються з дійсних чисел. Або у функції, вираженої у вигляді формули, ми не можемо включити будь-яке вхідне значення в області, що призвело б нас до поділу на 0.

Ми можемо візуалізувати домен як «зону утримання», яка містить «сировину» для «функціональної машини» та діапазон як іншу «зону утримання» для продуктів машини (рис.$\PageIndex{2}$).

альт — Малюнок$\PageIndex{2}$: Діаграма того, як функція пов'язує два відносини

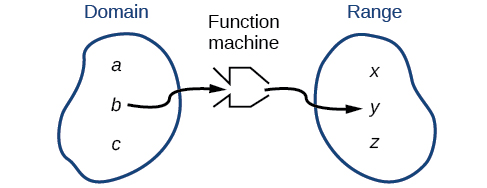
Ми можемо записати домен і діапазон в інтервальному позначенні, який використовує значення в дужках для опису набору чисел. У інтервальному позначенні ми використовуємо квадратну дужку [коли множина включає кінцеву точку та дужку (щоб вказати, що кінцева точка або не включена, або інтервал необмежений. Наприклад, якщо людина має 100 доларів, щоб витратити, йому потрібно буде висловити інтервал, який більше 0 і менше або дорівнює 100 і написати$\left(0, 100\right]$. Більш докладно поговоримо про інтервальні позначення пізніше.

Звернемо увагу на пошук області функції, рівняння якої забезпечено. Часто знаходження області таких функцій передбачає запам'ятовування трьох різних форм. По-перше, якщо функція не має знаменника або парного кореня, подумайте, чи можуть в області бути всі дійсні числа. По-друге, якщо у рівнянні функції є знаменник, виключіть значення в області, які змушують знаменник дорівнювати нулю. По-третє, якщо є парний корінь, подумайте про виключення значень, які зробили б радикальним і негативним.

Перш ніж ми почнемо, розглянемо умовності інтервальних позначень:

Найменший член з інтервалу записується першим.
Найбільший член в інтервалі пишеться другий, слідуючи за комою.
Дужки,$($ або$)$, використовуються для позначення того, що кінцева точка не включена, називається ексклюзивним.
Дужки,$[$ або$]$, використовуються для позначення того, що кінцева точка включена, називається включно.

Див. Рисунок$\PageIndex{3}$ для зведення інтервальних позначень.

Приклад$\PageIndex{1}$: Finding the Domain of a Function as a Set of Ordered Pairs

Знайдіть домен наступної функції:$\{(2, 10),(3, 10),(4, 20),(5, 30),(6, 40)\}$.

Рішення

Спочатку визначте вхідні значення. Вхідне значення є першою координатою в впорядкованій парі. Обмежень немає, так як впорядковані пари просто перераховані. Домен - це набір перших координат впорядкованих пар.

\[\{2,3,4,5,6\} \nonumber\]

Вправа$\PageIndex{1}$

Знайдіть домен функції:

\[\{(−5,4),(0,0),(5,−4),(10,−8),(15,−12)\} \nonumber\]

Відповідь: $\{−5, 0, 5, 10, 15\}$

Як: Задано функцію, записану у формі рівняння, знайдіть область.

Визначте вхідні значення.
Визначте будь-які обмеження на введення і виключіть ці значення з домену.
Напишіть домен в інтервальній формі, якщо це можливо.

Приклад$\PageIndex{2}$: Finding the Domain of a Function

Знайдіть домен функції$f(x)=x^2−1$.

Рішення

Вхідне значення, показане змінною x у рівнянні, зводиться в квадрат, а потім результат знижується на одиницю. Будь-яке дійсне число може бути зведене в квадрат, а потім зменшуватися на одиницю, тому обмежень по області цієї функції немає. Домен являє собою набір дійсних чисел.

У інтервальній формі домен f дорівнює$(−\infty,\infty)$.

Вправа$\PageIndex{2}$

Знайдіть домен функції:

\[f(x)=5−x+x^3 \nonumber\]

Відповідь: $(−\infty,\infty)$

Інструкція: За умови функції, записаної у формі рівняння, що включає дріб, знайдіть область

Визначте вхідні значення.
Визначте будь-які обмеження на введення. Якщо у формулі функції є знаменник, встановіть знаменник рівний нулю і вирішіть для x. Якщо формула функції містить парний корінь, встановіть радикад більше або дорівнює 0, а потім вирішуйте.
Запишіть домен в інтервальній формі, не забудьте виключити з домену будь-які обмежені значення.

Приклад$\PageIndex{3}$: Finding the Domain of a Function Involving a Denominator

Знайдіть домен функції$f(x)=\dfrac{x+1}{2−x}$.

Рішення

Коли є знаменник, ми хочемо включити тільки значення вхідних даних, які не змушують знаменник бути нулем. Отже, виставимо знаменник рівним 0 і вирішимо для х.

\[ \begin{align*} 2−x=0 \\[4pt] −x &=−2 \\[4pt] x&=2 \end{align*}\]

Тепер ми виключимо 2 з домену. Відповіді - це всі дійсні числа, де$x<2$ або$x>2$. Ми можемо використовувати символ, відомий як союз$\cup$, для об'єднання двох наборів. У інтервальних позначеннях записуємо рішення:$(−\infty,2)∪(2,\infty)$.

$[Лінійний графік f (x).]$

У інтервальній формі домен f дорівнює$(−\infty,2)\cup(2,\infty)$.

Вправа$\PageIndex{3}$

Знайдіть домен функції:

\[f(x)=\dfrac{1+4x}{2x−1} \nonumber\]

Відповідь: \[(−\infty,\dfrac{1}{2})\cup(\dfrac{1}{2},\infty) \nonumber\]

Як: За умови функції, записаної у формі рівняння, включаючи парний корінь, знайдіть домен.

Визначте вхідні значення.
Так як є парний корінь, виключіть будь-які дійсні числа, які призводять до негативного числа в радиканді. Встановіть радіканд більше або рівний нулю і вирішіть для x.
Рішення (и) є областю функції. Якщо є можливість, напишіть відповідь в інтервальній формі.

Приклад$\PageIndex{4}$: Finding the Domain of a Function with an Even Root

Знайдіть домен функції:

\[f(x)=\sqrt{7-x} \nonumber .\]

Рішення

Коли в формулі є парний корінь, виключаємо будь-які дійсні числа, які призводять до негативного числа в радиканді.

Встановіть радіканд більше або рівний нулю і вирішіть для x.

\[ \begin{align*} 7−x&≥0 \\[4pt] −x&≥−7\\[4pt] x&≤7 \end{align*}\]

Тепер ми виключимо будь-яке число більше 7 з домену. Відповіді всі дійсні числа менше або рівні 7, або$\left(−\infty,7\right]$.

Вправа$\PageIndex{4}$

Пошук домену функції

\[f(x)=\sqrt{5+2x}. \nonumber\]

Відповідь: \[\left[−2.5,\infty\right) \nonumber\]

Питання і відповіді: Чи можуть бути функції, в яких домен і діапазон взагалі не перетинаються?

Так. Наприклад, функція$f(x)=-\dfrac{1}{\sqrt{x}}$ має набір усіх позитивних дійсних чисел як область, а набір усіх від'ємних дійсних чисел - діапазон. Як більш екстремальний приклад, входи та виходи функції можуть бути абсолютно різними категоріями (наприклад, назви робочих днів як входів і чисел як виходів, як на графіку відвідуваності), в таких випадках домен і діапазон не мають спільних елементів.

Використання позначень для визначення домену та діапазону

У попередніх прикладах ми використовували нерівності та списки для опису області функцій. Ми також можемо використовувати нерівності або інші твердження, які можуть визначати набори значень або даних, щоб описати поведінку змінної в нотації set-builder. Наприклад,$\{x|10≤x<30\}$ описує поведінку x у позначеннях set-builder. $\{\}$Фігурні дужки читаються як «множина», а вертикальна смуга$|$ читається як «така, що», тому ми б читали$ \{x|10≤x<30\}$ як «набір значень x, такий, що 10 менше або дорівнює x, а x менше 30».

Рисунок$\PageIndex{4}$ порівнює позначення нерівності, множинні позначення та інтервальні позначення.

Рисунок$\PageIndex{4}$: Короткий зміст позначень для нерівностей, множинний конструктор та інтервал.

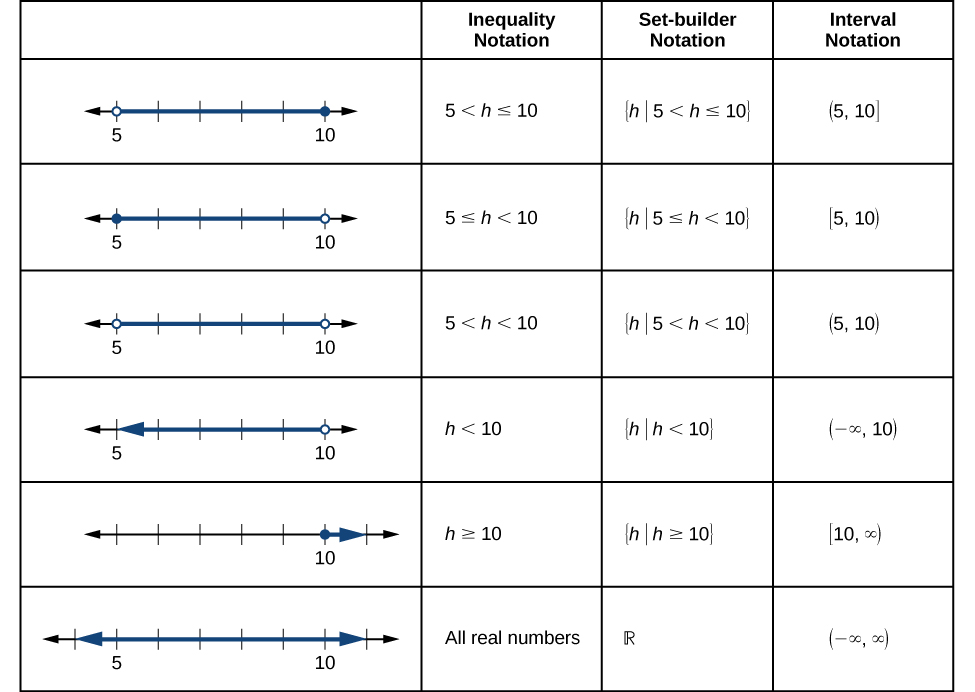
Для об'єднання двох інтервалів за допомогою позначення нерівності або позначення set-builder ми використовуємо слово «або». Як ми бачили в попередніх прикладах, ми використовуємо символ об'єднання$\cup$, для об'єднання двох незв'язаних інтервалів. Наприклад, об'єднання наборів$\{2,3,5\}$ і$\{4,6\}$ є безліччю$\{2,3,4,5,6\}$. Це сукупність всіх елементів, які належать до того чи іншого (або обох) вихідних двох множин. Для множин з кінцевою кількістю таких елементів елементи не повинні бути перераховані у порядку зростання числового значення. Якщо вихідні два набори мають деякі спільні елементи, ці елементи повинні бути перераховані лише один раз у наборі об'єднань. Для множин дійсних чисел на інтервалах іншим прикладом об'єднання є

\[\{x| |x|≥3\}=\left(−\infty,−3\right]\cup\left[3,\infty\right)\]

Позначення Set-Builder та інтервальні позначення

Позначення Set-builder - це метод вказівки набору елементів, що задовольняють певній умові. Він приймає форму,$\{x|\text{ statement about x}\}$ яка читається як: «множина всіх х таким чином, що твердження про х є істинним». Наприклад,

\[\{x|4<x≤12\} \nonumber\]

Інтервальне позначення - це спосіб опису множин, які включають всі дійсні числа між нижньою межею, яка може бути включена або не може бути включена, і верхньою межею, яка може бути включена або не може бути включена. Значення кінцевої точки вказані між дужками або дужками. Квадратна дужка вказує на включення до множини, а дужка - виключення з множини. Наприклад,

\[\left(4,12\right] \nonumber\]

$альт$ Задано лінійний графік, опишіть множину значень за допомогою інтервальних позначень.

Визначте інтервали, які потрібно включити в набір, визначивши, де важка лінія перекриває реальну лінію.
У лівому кінці кожного інтервалу використовуйте [з кожним кінцевим значенням, яке буде включено до множини (суцільна точка) або (для кожного виключеного кінцевого значення (відкрита точка).
У правому кінці кожного інтервалу використовуйте] з кожним кінцевим значенням, яке буде включено до множини (заповнена точка) або) для кожного виключеного кінцевого значення (відкрита точка).
Використовуйте символ об'єднання,$\cup$ щоб об'єднати всі інтервали в один набір.

Приклад$\PageIndex{5}$: Describing Sets on the Real-Number Line

Опишіть інтервали значень, показаних на малюнку,$\PageIndex{5}$ використовуючи позначення нерівності, множинні позначення та інтервальні позначення.

[Лінійний графік <span перекладати= — Малюнок$\PageIndex{5}$: Лінійний графік$1≤x≤3 \text{ or }x>5$.

Рішення

Щоб описати значення$x$, включені в показані інтервали, ми б сказали, «$x$це дійсне число більше або дорівнює 1 і менше або дорівнює 3, або дійсне число більше 5».

Нерівність

\[1≤x≤3 \text{ or }x>5 \nonumber\]

Позначення Set-Builder

\[\{x|1≤x≤3 \text{ or } x>5\}\nonumber\]

Інтервальні позначення

\[[1,3]\cup(5,\infty)\nonumber\]

Пам'ятайте, що при написанні або читанні інтервальних позначень використання квадратної дужки означає, що межа включена в множину. Використання дужки означає, що межа не включена в множину.

Вправа$\PageIndex{5}$

Задано рисунок$\PageIndex{6}$, вкажіть графічний набір у

слова
набір позначення будівельника
інтервальні позначення

[Лінійний графік -2<= x, -1<=x<3.] — Малюнок$\PageIndex{6}$: Лінійний графік$-2{\leq}x$,$-1{\leq}x<3$ .leq} x\),$-1{\leq}x<3$.

Відповідь на: Значення, які менше або рівні —2, або значення, які більше або рівні —1 і менше 3;
Відповідь б: $\{x|x≤−2 or −1≤x<3\}$
Відповідь c: $\left(−∞,−2\right]\cup\left[−1,3\right)$

Пошук домену та діапазону з графіків

Ще один спосіб ідентифікувати область і діапазон функцій - за допомогою графіків. Оскільки домен посилається на набір можливих вхідних значень, область графіка складається з усіх вхідних значень, показаних на осі x. Діапазон - це набір можливих вихідних значень, які відображаються на осі y. Майте на увазі, що якщо графік продовжується за межі частини графіка, яку ми можемо бачити, область та діапазон можуть бути більшими за видимі значення. Див$\PageIndex{7}$. Малюнок.

[Графік многочлена, який показує вісь x - це область, а вісь y - діапазон] — Рисунок$\PageIndex{7}$: Графік многочлена, який показує вісь x - область, а вісь y - діапазон

Ми можемо спостерігати, що граф простягається горизонтально від −5 вправо без обмежень, тому домен є$\left[−5,∞\right)$. Вертикальна протяжність графіка - це всі значення діапазону 5 і нижче, тому діапазон є$\left(−∞,5\right]$. Зауважте, що домен і діапазон завжди записуються від менших до більших значень, або зліва направо для домену, а знизу графіка до верхньої частини графіка для діапазону.

Приклад$\PageIndex{6A}$: Finding Domain and Range from a Graph

Знайдіть область і діапазон функції f, графік якої показаний на малюнку 1.2.8.

[Графік функції з (-3, 1].] — Малюнок$\PageIndex{8}$: Графік функції з (-3, 1].

Рішення

Ми можемо спостерігати, що горизонтальна протяжність графіка становить —3 до 1, тому область f є$\left(−3,1\right]$.

Вертикальний ступінь графіка дорівнює від 0 до —4, тому діапазон дорівнює$\left[−4,0\right)$. Див$\PageIndex{9}$. Малюнок.

[Графік попередньої функції показує область і діапазон.] — Малюнок$\PageIndex{9}$: Графік попередньої функції показує область і діапазон

Приклад$\PageIndex{6B}$: Finding Domain and Range from a Graph of Oil Production

Знайдіть область і діапазон функції f, графік якої показаний на рис$\PageIndex{10}$.

[Графік видобутку сирої нафти на Алясці, де вісь y становить тисячі барелів на день, а -вісь - роки.] — Рисунок$\PageIndex{10}$: Графік видобутку сирої нафти на Алясці, де вісь y становить тисячу барелів на день, а -вісь - роки (кредит: зміна роботи Управлінням енергетичної інформації США)

Рішення

Вхідна величина вздовж горизонтальної осі - «років», яку ми представляємо зі змінною t для часу. Вихідна кількість - «тисячі барелів нафти на день», яку ми представляємо зі змінною b для барелів. Графік може продовжувати ліворуч і праворуч за межами того, що розглядається, але на основі видимої частини графіка ми можемо визначити область як$1973≤t≤2008$ і діапазон як приблизно$180≤b≤2010$.

У інтервальних позначеннях домен є$[1973, 2008]$, а діапазон приблизно$[180, 2010]$. Для домену та діапазону ми наближаємо найменші та найбільші значення, оскільки вони не потрапляють точно на лінії сітки.

Вправа$\PageIndex{6}$

Задано рисунок$\PageIndex{11}$, визначити домен і діапазон за допомогою інтервальних позначень.

[Графік збільшення світового населення, де вісь y представляє мільйони людей, а вісь x - рік.] — Малюнок$\PageIndex{11}$: Графік збільшення світового населення, де вісь y представляє мільйони людей, а вісь x - рік.

Відповідь

домен =$[1950,2002]$

діапазон =$[47,000,000,89,000,000]$

$альт$ Чи може домен та діапазон функції бути однаковими?

Так. Наприклад, домен і діапазон функції кореня куба є сукупністю всіх дійсних чисел.

Пошук доменів та діапазонів функцій інструментарію

Тепер ми повернемося до нашого набору функцій інструментарію для визначення домену та діапазону кожної з них.

[Постійна функція f (x) = c.] — Малюнок$\PageIndex{12}$: Постійна функція$f(x)=c$.

Для постійної функції$ f(x)=c$ домен складається з усіх дійсних чисел, обмежень на введення немає. Єдиним вихідним значенням є константа$c$, тому діапазон - це набір$\{c\}$, який містить цей єдиний елемент. У інтервальних позначеннях це записується як$[c,c]$, інтервал, який і починається, і закінчується$c$.

$[Функція ідентичності f (x) =x.]$
Малюнок$\PageIndex{13}$: Функція ідентичності f (x) = x.

Для функції$f(x)=x$ ідентичності немає обмежень на$x$. І домен, і діапазон є сукупністю всіх дійсних чисел.

[Абсолютна функція f (x) =|x|.] — Малюнок$\PageIndex{14}$: Абсолютна функція$f(x)=|x|$.

Для функції$f(x)=|x|$ абсолютного значення немає обмежень на$x$. Однак, оскільки абсолютне значення визначається як відстань від 0, вихід може бути лише більшим або рівним 0.

[квадратична функція f (x) = x ^ 2] — Малюнок$\PageIndex{15}$: Квадратична функція$f(x)=x^2$.

Для квадратичної функції область - це всі дійсні числа$f(x)=x^2$, оскільки горизонтальна протяжність графіка - це ціла дійсна числова лінія. Оскільки графік не містить від'ємних значень для діапазону, діапазон є лише невід'ємними дійсними числами.

[Кубічна функція f (x) -x^3.] — Малюнок$\PageIndex{16}$: Кубічна функція$f(x)-x^3$.

Для кубічної функції доменом є всі дійсні числа$f(x)=x^3$, оскільки горизонтальна протяжність графіка - це ціла дійсна числова лінія. Те ж саме стосується вертикальної протяжності графіка, тому область і діапазон включають всі дійсні числа.

[Зворотна функція f (x) = 1/x.] — Малюнок$\PageIndex{17}$: Зворотна функція$f(x)=\dfrac{1}{x}$.

Для зворотної функції$f(x)=\dfrac{1}{x}$ ми не можемо розділити на 0, тому ми повинні виключити 0 з домену. Крім того, 1 поділений на будь-яке значення ніколи не може бути 0, тому діапазон також не буде включати 0. У нотації set-builder ми також могли б написати$\{x| x≠0\}$, набір всіх дійсних чисел, які не є нулем.

[Взаємна квадратна функція...] — Малюнок$\PageIndex{18}$: Функція зворотного квадрата$f(x)=\dfrac{1}{x^2}$

Для зворотної квадратної функції$f(x)=\dfrac{1}{x^2}$ ми не можемо розділити на 0, тому ми повинні виключити 0 з домену. Також немає x, який може дати вихід 0, тому 0 також виключається з діапазону. Зверніть увагу, що висновок цієї функції завжди позитивний через квадрат у знаменнику, тому діапазон включає тільки позитивні числа.

$[Функція квадратного кореня f (x) = sqrt (x).]$
Малюнок$\PageIndex{19}$: Функція квадратного кореня$f(x)=\sqrt{(x)}$.

Для функції квадратного кореня$f(x)=\sqrt{x}$ ми не можемо взяти квадратний корінь від'ємного дійсного числа, тому домен повинен бути 0 або більше. Діапазон також виключає негативні числа, оскільки квадратний корінь позитивного числа$x$ визначається як додатне, хоча квадрат негативного числа$−\sqrt{x}$ також дає нам$x$.

[Корінь куба функція f (x) =x^ (1/3).] — Малюнок$\PageIndex{20}$: Функція кореня куба$f(x)=\sqrt[3]{x}$.

Для функції$f(x)=\sqrt[3]{x}$ кореня куба домен і діапазон включають всі дійсні числа. Зауважте, що немає проблем з отриманням кубового кореня або будь-якого непарного цілого кореня з від'ємним числом, а отриманий результат є від'ємним (це непарна функція).

$альт$ Задано формулу для функції, визначають область і діапазон.

Виключити з домену будь-які вхідні значення, які призводять до поділу на нуль.
Виключити з домену будь-які вхідні значення, які мають нереальні (або невизначені) числові виходи.
Використовуйте допустимі вхідні значення для визначення діапазону вихідних значень.
Подивіться на графік функцій та значення таблиці, щоб підтвердити фактичну поведінку функції.

Пошук домену та діапазону за допомогою функцій інструментарію

Знайдіть домен і діапазон доменів$f(x)=2x^3−x$.

Рішення

Обмежень щодо домену немає, так як будь-яке дійсне число може бути кубовим, а потім відніматися з результату.

Домен є$(−\infty,\infty)$ і діапазон також$(−\infty,\infty)$.

Приклад$\PageIndex{7B}$: Finding the Domain and Range

Знайдіть домен і діапазон доменів$f(x)=\frac{2}{x+1}$.

Рішення

Ми не можемо оцінити функцію за −1, оскільки ділення на нуль не визначено. Домен є$(−\infty,−1)\cup(−1,\infty)$. Оскільки функція ніколи не дорівнює нулю, ми виключаємо 0 з діапазону. Асортимент є$(−\infty,0)\cup(0,\infty)$.

Приклад$\PageIndex{7C}$: Finding the Domain and Range

Знайдіть домен і діапазон доменів$f(x)=2 \sqrt{x+4}$.

Рішення

Ми не можемо взяти квадратний корінь від'ємного числа, тому значення всередині радикала має бути невід'ємним.

$x+4≥0$коли$x≥−4$

Домен$f(x)$ is$[−4,\infty)$.

Потім знаходимо діапазон. Ми знаємо$f(−4)=0$, що, і значення функції збільшується зі$x$ збільшенням без будь-якої верхньої межі. Робимо висновок, що діапазон f дорівнює$\left[0,\infty\right)$.

Аналіз

Малюнок$\PageIndex{19}$ представляє функцію$f$.

" src="https://math.libretexts.org/@api/dek..._01_02_020.jpg">

Рисунок$\PageIndex{19}$: Графік функції квадратного кореня в$(-4, 0)$.

Вправа$\PageIndex{7}$

Пошук домену та діапазону

$f(x)=\sqrt{−2−x}$.

Відповідь

домен:$\left(−\infty,-2\right]$

Діапазон:$\left[0,\infty\right)$

Графічні кусково визначені функції

Іноді ми стикаємося з функцією, яка вимагає більше однієї формули для отримання заданого результату. Наприклад, у функціях інструментарію ми ввели функцію абсолютного значення$f(x)=|x|$. З областю всіх дійсних чисел і діапазоном значень, більших або рівних 0, абсолютне значення може бути визначено як величина, або модуль, значення дійсного числа незалежно від знака. Це відстань від 0 на числовому рядку. Усі ці визначення вимагають, щоб вивід був більшим або рівним 0.

Якщо ми вводимо 0, або додатне значення, вихід такий же, як і вхід.

\[ f(x)=x \; \text{ if } \; x≥0 \nonumber \]

Якщо ми вводимо від'ємне значення, вихід протилежний входу.

\[ f(x) = -x \; \text { if } \; x < 0 \nonumber \]

Оскільки для цього потрібні два різні процеси або частини, функція абсолютного значення є прикладом кускової функції. Кускова функція - це функція, в якій більше однієї формули використовується для визначення вихідних даних над різними частинами області.

Ми використовуємо кускові функції для опису ситуацій, в яких правило або зв'язок змінюється, коли вхідне значення перетинає певні «межі». Наприклад, ми часто стикаємося з ситуаціями в бізнесі, для яких вартість за штуку певного товару знижується, коли замовлене число перевищує певну вартість. Податкові дужки - ще один реальний приклад кускових функцій. Для прикладу розглянемо просту систему оподаткування, при якій доходи до 10 000 доларів оподатковуються під 10%, а будь-який додатковий дохід оподатковується під 20%. Податок на загальний дохід S буде$0.1S$ якщо$S≤$10,000$ і$$1000+0.2(S−$10,000)$ якщо$S>$10,000$.

Кусково функція

Кускова функція - це функція, в якій для визначення вихідних даних використовується більше однієї формули. Кожна формула має свій домен, а область функції - об'єднання всіх цих менших доменів. Ми відзначаємо цю ідею так:

\[f(x)= \begin{cases} \text{formula 1} & \text{if x is in domain 1} \\ \text{formula 2} &\text{if x is in domain 2} \\ \text{formula 3} &\text{if x is in domain 3}\end{cases} \nonumber \]

У кусковому позначенні функція абсолютного значення дорівнює

\[|x|= \begin{cases} x & \text{if $x \geq 0$} \\ -x &\text{if $x<0$} \end{cases} \nonumber \]

$альт$ Задано кускову функцію, запишіть формулу і визначте домен для кожного інтервалу.

Визначте інтервали, для яких застосовуються різні правила.
Визначте формули, які описують, як обчислити вихід з вхідних даних в кожному інтервалі.
Використовуйте фігурні дужки та if-оператори для запису функції.

Приклад$\PageIndex{8A}$: Writing a Piecewise Function

Музей стягує 5 доларів США з людини за екскурсію з групою від 1 до 9 осіб або фіксовану плату в розмірі 50 доларів США для групи з 10 і більше людей. Напишіть функцію, що стосується кількості людей$n$, до вартості,$C$.

Рішення

Будуть потрібні дві різні формули. Для$n$ -значень під 10,$C=5n$. Для значень n, які дорівнюють 10 або більше,$C=50$.

\[C(n)= \begin{cases} 5n & \text{if $n < 10$} \\ 50 &\text{if $n\geq10$} \end{cases} \nonumber \]

Аналіз

Функція представлена на рис$\PageIndex{20}$. Графік являє собою діагональну лінію від$n=0$ до$n=10$ і постійну після цього. У цьому прикладі дві формули узгоджуються в місці зустрічі$n=10$, де, але не всі кускові функції мають цю властивість.

[Графік С (n).] — Малюнок$\PageIndex{20}$

Приклад$\PageIndex{8B}$: Working with a Piecewise Function

Компанія стільникового телефону використовує функцію нижче, щоб визначити вартість, C, в доларах для g гігабайт передачі даних.

\[C(g)= \begin{cases} 25 & \text{if $0<g<2$} \\ 25+10(g-2) &\text{if $g\geq2$} \end{cases} \nonumber \]

Знайдіть вартість використання 1,5 гігабайт даних і вартість використання 4 гігабайт даних.

Рішення

Щоб дізнатися вартість використання 1,5 гігабайт даних$C(1.5)$, ми спочатку подивимося, в яку частину домену потрапляє наш вхід. Оскільки 1.5 менше 2, ми використовуємо першу формулу.

\[C(1.5)=$25 \nonumber \]

Щоб знайти вартість використання 4 гігабайт даних, C (4), ми бачимо, що наш вхід 4 більше 2, тому використовуємо другу формулу.

\[C(4)=25+10(4−2)=$45 \nonumber \]

Аналіз

Функція представлена на рис$\PageIndex{21}$. Ми можемо бачити, де функція змінюється від постійної до зміщеної і розтягнутої ідентичності в$g=2$. Ми будуємо графіки для різних формул на загальному наборі осей, переконавшись, що кожна формула застосовується на належній області.

[Графік C (g)] — Малюнок$\PageIndex{21}$

$альт$ Задано кускову функцію, намалюйте графік.

Вкажіть на осі x межі, визначені інтервалами на кожному фрагменті домену.
Для кожного фрагмента області, графік на цьому інтервалі, використовуючи відповідне рівняння, що відноситься до цього фрагмента. Не графуйте дві функції протягом одного інтервалу, оскільки це порушить критерії функції.

Приклад$\PageIndex{8C}$: Graphing a Piecewise Function

Намалюйте графік функції.

\[f(x)= \begin{cases} x^2 & \text{if $x \leq 1$} \\ 3 &\text{if $1<x\leq2$} \\ x &\text{if $x>2$} \end{cases} \nonumber \]

Рішення

Кожна з функцій компонента є з нашої бібліотеки функцій інструментарію, тому ми знаємо їх форми. Ми можемо уявити собі графіки кожної функції, а потім обмежити графік до зазначеної області. У кінцевих точках області ми малюємо відкриті кола, щоб вказати, де кінцева точка не включена через нерівність менше або більше, ніж; ми малюємо замкнуте коло, де кінцева точка включена через нерівність менше, ніж або рівне або більше, ніж або рівне.

$\PageIndex{20}$На малюнку показані три складові частини кускової функції, розміщені на окремих системах координат.

$[Графік кожної частини кускової функції f (x)]$
Малюнок$\PageIndex{20}$: Графік кожної частини кускової функції f (x)

(а)$ f(x)=x^2$ якщо$x≤1$; (б)$f(x)=3$ якщо$1< x≤2$; (c)$f(x)=x$ якщо$x>2$

Тепер, коли ми накидали кожен шматок окремо, ми об'єднуємо їх в одній координатній площині. Див$\PageIndex{21}$. Малюнок.

[Графік всієї функції.] — Малюнок$\PageIndex{21}$: Графік всієї функції.

Аналіз

Зверніть увагу, що графік дійсно проходить тест вертикальної лінії навіть в точках$x=1$$(1,3)$ і$x=2$ тому, що точки і не$(2,2)$ є частиною графіка функції, хоча$(1,1)$ і$(2, 3)$ є.

Вправа$\PageIndex{8}$

Графік наступної кускової функції.

\[f(x)= \begin{cases} x^3 & \text{if $x < -1$} \\ -2 &\text{if $-1<x<4$} \\ \sqrt{x} &\text{if $x>4$} \end{cases} \nonumber \]

Відповідь: $[Графік f (x).]$
Малюнок$\PageIndex{22}$

$альт$ Чи можна застосувати більше однієї формули з кускової функції до значення в області?

Ні. Кожному значенню відповідає одне рівняння в кусковій формулі.

Ключові поняття

Область функції включає всі дійсні вхідні значення, які не змусять нас спробувати невизначену математичну операцію, наприклад, ділення на нуль або взяття квадратного кореня від'ємного числа.
Домену функції можна визначити шляхом перерахування вхідних значень набору впорядкованих пар.
Домену функції також можна визначити шляхом ідентифікації вхідних значень функції, записаної як рівняння.
Інтервальні значення, представлені на числовому рядку, можуть бути описані за допомогою позначення нерівності, нотації множинного конструктора та інтервальних нотацій.
Для багатьох функцій область і діапазон можна визначити за графіком.
Розуміння функцій інструментарію може бути використано для пошуку домену та діапазону пов'язаних функцій.
Кускова функція описується більш ніж однією формулою.
Кусково функція може бути позначена за допомогою кожної алгебраїчної формули на призначеному піддомені.

Виноски

1 Цифри: де зустрічаються дані та кінобізнес. «Історія касових зборів для фільмів жахів». http://www.the-numbers.com/market/genre/Horror. Доступ до 24/3/2014
2 www.eia.gov/ДНАВ/ПЕТ/Гіст/Леа... s=MCRFPak2&F = A.

Глосарій

інтервальні позначення: метод опису множини, який включає всі числа між нижньою межею і верхньою межею; нижня і верхня значення перераховані між дужками або дужками, квадратна дужка, що вказує включення в набір, і дужки, що вказують виключення

кусково функція: функція, в якій для визначення вихідних даних використовується більше однієї формули

набір позначення будівельника: метод опису множини правилом, якому підкоряються всі його члени; він набуває вигляду {x| оператор about x}