8.8: Додатки

П'ятиступінчастий метод

Зараз ми в змозі вивчити деякі застосування раціональних рівнянь. Деякі з цих проблем матимуть практичне застосування, а інші призначені як розробники логіки.

Ми будемо застосовувати п'ятикроковий метод для вирішення словесних задач.

П'ятиступінчастий метод

П'ятиступінчастий метод

1. Представляють всі невідомі величини в терміні x або якоїсь іншої літери.
2. Переведіть словесні фрази на математичні символи і сформуйте рівняння.
3. Розв'яжіть це рівняння.
4. Перевірте рішення, підставивши результат в початкову постановку задачі.
5. Напишіть висновок.

Пам'ятайте, крок 1 дуже важливий: завжди

Ввести змінну.

Набір зразків A

Приклад$\PageIndex{1}$

Коли одне і те ж число додається до нумератора і знаменника дробу$\dfrac{3}{5}$, то результат якщо$\dfrac{7}{9}$. Що таке число, яке додається?

Крок 1: Нехай$x =$ число додається.

\ (\ begin {масив} {Flushleft}
\ текст {Крок 2:} &\ dfrac {3+x} {5+x} &=\ dfrac {7} {9}\
\ текст {Крок 3:} &\ dfrac {3+x} {5+x} &=\ dfrac {7} {9} &\ text {Виключене значення} -5\
&&&\ text {Помножити кожен член на} 9 (5+ x)\\
& 9 (5 + х)\ cdot\ dfrac {3 + х} {5 + х} &= 9 (5 + х)\ cdot\ dfrac {7} {9}\\
& 9 (3 + x) &= 7 (5 + x)\\
& 27 + 9x &= 35 + 7x\\
& 2x &= 8\\
& x &= 4 &\ text {Перевірте це потенційне рішення}\
\ text {Крок 4:} &\ dfrac {3 + 4} {5 + 4} &=\ dfrac {7} {9} &\ text {Так, це правильно}\
\ текст {Крок 5: Додано число} 4
\ end {масив}\)

Практика Set A

Це ж число додається до чисельника і знаменника дробу$\dfrac{4}{9}$. Результат є$\dfrac{2}{3}$. Що таке число, яке додається?

Завдання практики$\PageIndex{1}$

Крок 1: Нехай$x =$

Крок 2:

Крок 3:

Крок 4:

Крок 5: Додано число - __.

Відповідь

Додано число - 6.

Набір зразків B

Приклад$\PageIndex{2}$

Дві третини числа додаються до зворотного числа врожайності$\dfrac{25}{6}$. Що таке число?

Крок 1: Нехай$x =$ число.

Крок 2: Нагадаємо, що зворотним числом$x$ є число$\dfrac{1}{x}$.

$\dfrac{2}{3} \cdot x + \dfrac{1}{x} = \dfrac{25}{6}$

\ (\ begin {масив} {Flushleft}
\ текст {Крок 3:} &\ dfrac {2} {3}\ cdot x +\ dfrac {1} {x} &=\ dfrac {25} {6} &\ текст {РК-дисплей} 6x\ текст {. Помножте кожен член на} 6x\\
& 6x\ ddot\ drac {2} {3} x + 6x\ ddot\ drac {1} {x} &= 6x\ ddot\ drac {25} {6}\
& 4x^2 + 6 &= 25x &\ text {Розв'яжіть це бездробове квадратне рівняння для отримання потенційних розв'язків. (Використовуйте властивість нульового фактора.) \\
& 4x^2 - 25x + 6 &= 0\\
& (4x - 1) (x - 6) &= 0\\
& x &=\ dfrac {1} {4}, 6 &\ text {Перевірте ці потенційні рішення}
\ end {масив}\)

Крок 4: Підставляючи вихідне рівняння, може бути, що обидва рішення перевіряють.

Крок 5: Є два рішення:$\dfrac{1}{4}$ і$6$.

Практика Set B

Завдання практики$\PageIndex{2}$

Сім половин числа, доданих до зворотного числа, виходить$\dfrac{23}{6}$. Що таке число?

Крок 1: Нехай$x =$

Крок 2:

Крок 3:

Крок 4:

Крок 5: Число є.

Відповідь

Є два числа:$\dfrac{3}{7}, \dfrac{2}{3}$

Набір зразків C

Приклад$\PageIndex{3}$

Людина А, працюючи поодинці, може залити бетонну доріжку за 6 годин. Людина Б, працюючи поодинці, може залити ту ж доріжку за 4 години. Скільки часу знадобиться обом людям, щоб залити бетонну доріжку, що працює разом?

Крок 1: Нехай$x =$ кількість годин, щоб залити бетонну доріжку, що працює разом (оскільки це те, що ми шукаємо).

Крок 2: Якщо людина А може виконати роботу за 6 годин, А може завершити$\dfrac{1}{6}$ роботу за 1 годину. Якщо людина Б може виконати роботу за 4 години, B може завершити$\dfrac{1}{4}$ роботу за 1 годину. Якщо A і B, працюючи разом, можуть виконати роботу за$x$ годинами, вони можуть завершити$\dfrac{1}{x}$ роботу за 1 годину. Помістивши ці три факти у форму рівняння, ми маємо:

$\dfrac{1}{6} + \dfrac{1}{4} = \dfrac{1}{x}$

\ (\ почати {масив} {Flushleft}
\ текст {Крок 3:} &\ dfrac {1} {6} +\ dfrac {1} {4} &=\ dfrac {1} {x} &\ text {Виключене значення 0}\\
& 12x\ cdot\ dfrac {1} {6} +\ dfrac {12x}\ cdot\ dfrac {1} {4} &= 12x\ ddot\ dfrac {1} {x}\\
& 2x + 3x &= 12 &\ текст { Розв'яжіть це бездробове рівняння для отримання потенційних розв'язків}\\

& 5x &= 12\\ & x &=\ dfrac {12} {5}\ text {або} x=2\ dfrac {2} {5} &\ text {Перевірте це потенційне рішення.}
\\ text {Крок 4:} &\ dfrac {1} {6} +\ dfrac {1}} &=\ dfrac {1} {x}\\
&\ dfrac {1} {6} +\ dfrac {1} {4} =\ dfrac {\ frac {1} {12}} {5}. &\ text {Це правильно? }\\
&\ dfrac {1} {6} +\ dfrac {1} {4} &=\ dfrac {5} {12} &\ текст {РК-дисплей} 12\ текст {. Чи правильно це? }\\
&\ dfrac {2} {12} +\ dfrac {3} {12} &=\ dfrac {5} {12} &\ text {Це правильно? }\\
&\ dfrac {5} {12} &=\ dfrac {5} {12} &\ text {Так, це правильно}
\ end {масив}\)

Крок 5: Працюючи разом, А і В можуть залити бетонну доріжку за$2\dfrac{2}{5}$ години.

Практика Set C

Завдання практики$\PageIndex{3}$

Людина А, працюючи поодинці, може залити бетонну доріжку за 9 годин. Людина Б, працюючи поодинці, може залити ту ж доріжку за 6 годин. Скільки часу знадобиться обом людям, щоб залити бетонну доріжку, що працює разом?

Крок 1:

Крок 2:

Крок 3:

Крок 4:

Крок 5: Робота разом, A і B.

Відповідь

Працюючи разом, А і В можуть залити бетонну доріжку в$3\dfrac{3}{5}$ годину.

Набір зразків D

Приклад$\PageIndex{4}$

Впускний патрубок може заповнити резервуар для води за 12 годин. Вихідний патрубок може злити бак за 20 годин. Якщо обидві труби відкриті, скільки часу знадобиться для заповнення бака?

Крок 1: Нехай x = кількість годин, необхідних для заповнення бака.

Крок 2: Якщо вхідна труба може заповнити резервуар за$12$ години, вона може заповнити$\dfrac{1}{12}$ резервуар за$1$ годину.

Якщо вихідний патрубок може злити бак за 20 годин, він може злити$\dfrac{1}{20}$ з бачка за$1$ годину.

Якщо обидві труби відкриті, на заповнення бака потрібні$x$ години. Так$\dfrac{1}{x}$ бак буде заповнений через$1$ годину.

Так як вода додається (впускний патрубок) і віднімається (вихідний патрубок) отримуємо

$\dfrac{1}{12} - \dfrac{1}{20} = \dfrac{1}{x}$

\ (\ begin {масив} {Flushleft}
\ текст {Крок 3:} &\ dfrac {1} {12} -\ dfrac {1} {20} &=\ dfrac {1} {x} &\ text {Виключене значення} 0\ text {. РК-дисплей} 60x\ текст {. Помножте кожен член на} 60x. \\
& 60x\ cdot\ dfrac {1} {12} - 60x\ cdot\ dfrac {1} {20} &= 60x\ cdot\ dfrac {1} {x}\
& 5x - 3x &= 60 &\ text {Розв'яжіть це бездробове рівняння для отримання потенційних розв'язків.}\\
& 2x &= 60\ & x &= 30\
& x &= 30 &\ текст { Перевірте це потенційне рішення}\
\ text {Крок 4:} &\ dfrac {1} {12} -\ dfrac {1} {20} &=\ dfrac {1} {x}\\
&\ dfrac {1} {12} -\ dfrac {1} {20} &=\ dfrac {1} {30} &\ text {LCD} 60 текст {. Чи правильно це? }\\
&\ dfrac {5} {60} -\ dfrac {3} {60} &=\ dfrac {1} {30} &\ text {Це правильно? }\\
&\ dfrac {1} {30} &=\ dfrac {1} {30} &\ text {Так, це правильно}
\ end {масив}\)

Крок 5: При відкритих обох трубах знадобиться кілька$30$ годин, щоб заповнити резервуар для води.

Практика Set D

Завдання практики$\PageIndex{4}$

Вхідний патрубок може заповнити резервуар для води за 8 годин, а випускна труба може злити бак за 10 годин. Якщо обидві труби відкриті, скільки часу знадобиться для заповнення бака?

Крок 1:

Крок 2:

Крок 3:

Крок 4:

Крок 5:

Відповідь

На заповнення ємності буде потрібно 40 годин.

Набір зразків E

Приклад$\PageIndex{5}$

Для виконання певної роботи людина A 3 години довше, ніж людина B. Працюючи разом, обидва можуть завершити роботу за 2 години. Скільки часу потрібно кожній людині, щоб завершити роботу, працюючи поодинці?

Крок 1: Нехай$x=$ час, необхідний для B, щоб завершити роботу, працюючи самостійно. Потім$(x+3) =$ час, необхідний для А, щоб завершити роботу, працюючи поодинці.

\ (\ почати {масив} {змив}
\ текст {Крок 2:} &\ dfrac {1} {x} +\ dfrac {1} {x+3} &=\ dfrac {1} {2}\\ текст {Крок 3:} &
\ dfrac {1} +\ dfrac {1} +\ dfrac {1} {x+3} &dfrac {1} {2} &\ text {Два виключені значення} 0\ text {і} -3\ text {. РК-дисплей} 2x (x+3)\\
& 2x (x+3)\ точка\ dfrac {1} {x} + 2x (x+3)\ точка\ dfrac {1} {x+3} &= 2x (x+3)\ ddot\ dfrac {1}\\
& 2 (x+3) + 2x &= x (x+3)\
& 2x+ 6 + 2x &= x ^ 2 + 3x &\ text {Це квадратне рівняння, яке можна вирішити за допомогою нуль- властивість фактора}\\
& 4x + 6 &= x ^ 2+ 3x\\
& x^2 - x - 6 &= 0\\
& (x-3) (x+2) &= 0\\
& (x-3) (x+2) &= 0\\
& x &= 3, -2 &\ text {Перевірте ці потенційні рішення}
\ end {масив}\)

Крок 4: Якщо$x = -2$ рівняння перевіряє, але навіть не має фізичного сенсу.

Якщо$x = 3$, рівняння перевіряє

$x = 3$і$x + 3 = 6$.

Крок 5: Людина Б може виконувати роботу за$3$ години, а людина А може виконувати роботу за$6$ години.

Практика Set E

Завдання практики$\PageIndex{5}$

Для виконання певного завдання людині А потрібно 4 години менше, ніж людина Б. Працюючи разом, обидва можуть виконати завдання за$\dfrac{8}{3}$ години. Скільки часу потрібно кожній людині, щоб виконати завдання, працюючи самостійно?

Крок 1:

Крок 2:

Крок 3:

Крок 4:

Крок 5:

Відповідь

Особа А, 4 год для виконання завдання; особа Б, 8 год виконати завдання.

Набір зразків F

Приклад$\PageIndex{6}$

Ширина прямокутника - це$\dfrac{1}{3}$ його довжина. Знайдіть розміри (довжину і ширину), якщо периметр дорівнює$16$ см.

Крок 1: Нехай$x=$ довжина. Потім$\dfrac{x}{3}=$ ширина.

Крок 2: Робимо ескіз прямокутника.

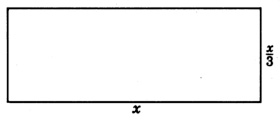
Периметр фігури - це загальна довжина навколо фігури.

\ (\ почати {масив} {Flushleft}
& x +\ dfrac {x} {3} + х +\ dfrac {x} {3} &= 16\\
& 2x +\ dfrac {2x} {3} &= 16
\\\ текст {Крок 3:} & 2x +\ dfrac {2x} {3} &= 16\\ текст {РК-дисплей {3} є} 3\\
& 3\ крапка 2х+ 3\ точка\ drac {2x} {3} &= 3\ точка 16\\
& 6x + 2x &= 48\\
& 8x &= 48\\
& x &= 6 &\ text {Перевірте це потенційне рішення.}
\\ text {Крок 4:} & 6 +\ dfrac {6} {3} +\ dfrac {6} {3} &= 16 &\ текст {Це правильно?}
& 6 + 2 + 6 + 2 &= 16 &\ текст {Це правильно?} \\
& 16 &= 16 &\ text {Так, це правильно.}
\ end {масив}\)

Так як$x = 6, \dfrac{x}{3} = \dfrac{6}{3} = 2$

Крок 5: Довжина$=6$ см і ширина$=2$ см.

Практика Набір F

Завдання практики$\PageIndex{6}$

Ширина прямокутника - це$\dfrac{1}{12}$ його довжина. Знайдіть розміри (довжину і ширину), якщо периметр$78$ футів.

Крок 1:

Крок 2:

Крок 3:

Крок 4:

Крок 5:

Відповідь

довжина = 36 футів, ширина = 3 фути.

Вправи

Для наступних завдань вирішуйте за допомогою п'ятикрокового методу.

Вправа$\PageIndex{1}$

Коли одне і те ж число додається як до чисельника, так і до знаменника дробу$\dfrac{3}{7}$, результат буде$\dfrac{2}{3}$. Що таке число?

Відповідь

Число додано є$5$.

Вправа$\PageIndex{2}$

Коли одне і те ж число додається як до чисельника, так і до знаменника дробу$\dfrac{5}{8}$, результат буде$\dfrac{3}{4}$. Що таке число?

Вправа$\PageIndex{3}$

Коли одне і те ж число додається як до чисельника, так і до знаменника дробу$\dfrac{3}{8}$, результат буде$\dfrac{1}{6}$. Що таке число?

Відповідь

Число додано є$−2$.

Вправа$\PageIndex{4}$

Коли одне і те ж число додається як до чисельника, так і до знаменника дробу$\dfrac{7}{9}$, результат буде$\dfrac{2}{3}$. Що таке число?

Вправа$\PageIndex{5}$

Коли одне і те ж число віднімається як до чисельника, так і знаменника дробу$\dfrac{1}{10}$, результат є$\dfrac{2}{3}$. Що таке число?

Відповідь

Число віднімається дорівнює$−17$.

Вправа$\PageIndex{6}$

Коли одне і те ж число віднімається як до чисельника, так і знаменника дробу$\dfrac{3}{4}$, результат є$\dfrac{5}{6}$. Що таке число?

Вправа$\PageIndex{7}$

Третина числа додається до зворотної кількості врожайності$\dfrac{13}{6}$. Що таке число?

Відповідь

$x= \dfrac{1}{2}, 6$

Вправа$\PageIndex{8}$

Чотири п'яті числа додаються до зворотної кількості врожайності$\dfrac{81}{10}$. Що таке число?

Вправа$\PageIndex{9}$

Половина числа додається до подвоєного зворотного числа$2$. Що таке число?

Відповідь

$2$

Вправа$\PageIndex{10}$

Одна четверта частина числа, що додається до чотирьох разів зворотного числа, дає$\dfrac{-10}{3}$. Що таке число?

Вправа$\PageIndex{11}$

Одна впускна труба може заповнити бак за 8 годин. Ще одна вхідна труба може заповнити бак за 5 годин. Скільки часу потрібно обом трубам, що працюють разом, щоб заповнити бак?

Відповідь

$3\dfrac{1}{13}$годин.

Вправа$\PageIndex{12}$

Одна труба може злити басейн за 12 годин. Інша труба може злити басейн за 15 годин. Скільки часу потрібно обидві труби, що працюють разом, щоб зливати басейн?

Вправа$\PageIndex{13}$

Змішувач може заповнити раковину у ванній за 1 хвилину. Злив може спорожнити раковину за 2 хвилини. Якщо і кран, і злив відкриті, скільки часу знадобиться для заповнення раковини?

Відповідь

дві хвилини

Вправа$\PageIndex{14}$

Змішувач може заповнити ванну за$6\dfrac{1}{2}$ лічені хвилини. Злив може спорожнити ванну за$8\dfrac{1}{3}$ лічені хвилини. Якщо і кран, і злив відкриті, скільки часу знадобиться для заповнення ванни?

Вправа$\PageIndex{15}$

Впускний патрубок може заповнити бак за 5 годин. Випускна труба може спорожнити бак за 4 години. Якщо обидві труби відкриті, чи можна заповнити бак? Поясніть.

Відповідь

Ні. $x=−20$годин.

Вправа$\PageIndex{16}$

Впускний патрубок може заповнити бак в$a$ одиниці часу. Випускна труба може спорожнити бак в$b$ одиниці часу. Якщо обидві труби відкриті, скільки одиниць часу потрібно для заповнення бака? Чи є обмеження на$a$ і$b$?

Вправа$\PageIndex{17}$

Кур'єр-хлопець, який працює один, може доставити весь свій товар за 6 годин. Ще один доставник, який працює один, може доставити такий же товар за 5 годин. Скільки часу буде потрібно хлопцям, щоб доставити всі товари, що працюють разом?

Відповідь

$2\dfrac{8}{11}$годин.

Вправа$\PageIndex{18}$

Космічний човник космонавт може виконати певний експеримент за 2 години. Ще один космонавт космічного човника, який не так знайомий з експериментом, може виконати його за$2\dfrac{1}{2}$ години. Працюючи разом, скільки часу знадобиться обом космонавтам, щоб виконати експеримент?

Вправа$\PageIndex{19}$

Одна людина може виконати завдання на 8 годин раніше, ніж інша людина. Працюючи разом, обидві людини можуть виконати завдання за 3 години. Скільки годин потрібно кожній людині, щоб виконати завдання, працюючи самостійно?

Відповідь

Перша особа: 12 годин; друга особа: 4 години

Вправа$\PageIndex{20}$

Знайдіть два послідовних цілих числа, такі, що дві третини меншого числа, доданого до іншого, дають 11.

Вправа$\PageIndex{21}$

Знайти два послідовних цілих числа, такі, що три чверті меншого числа, доданого до іншого, дають 29.

Відповідь

16,17

Вправа$\PageIndex{22}$

Ширина прямокутника - це$\dfrac{2}{5}$ його довжина. Знайти розміри, якщо периметр 42 метри.

Вправа$\PageIndex{23}$

Ширина прямокутника - це$\dfrac{3}{7}$ довжина. Знайдіть розміри, якщо периметр дорівнює 60 футам.

Відповідь

ширина = 9 футів; довжина = 21 фут

Вправа$\PageIndex{24}$

Дві сторони трикутника мають однакову довжину. Третя сторона в два рази довше, ніж будь-яка з двох інших сторін. Периметр трикутника - 56 дюймів. Яка довжина кожної сторони?

Вправа$\PageIndex{25}$

У трикутнику друга сторона на 3 дюйми довша, ніж перша сторона. Третя сторона -$\dfrac{3}{4}$ довжина другої сторони. Якщо периметр 30 дюймів, як довго кожна сторона?

Відповідь

сторона 1 = 9 дюймів; сторона 2 = 12 дюймів; сторона 3 = 9 дюймів

Вправа$\PageIndex{26}$

Тиск за рахунок поверхневого натягу в сферичній краплі рідини$T$ задається тим$P=\dfrac{2T}{r}$, де знаходиться поверхневий натяг рідини і$r$ радіус краплі. Якщо рідина є бульбашкою, вона має дві поверхні, і поверхневий натяг задається

$P = \dfrac{2T}{r} + \dfrac{2T}{r} = \dfrac{4T}{r}$

(а) Визначте тиск через поверхневий натяг в межах мильної бульбашки радіусом 2 дюймів і поверхневого натягу 28.
(b) Визначте радіус міхура, якщо тиск через поверхневий натяг становить 52, а поверхневий натяг - 39.

Вправа$\PageIndex{27}$

Рівняння$\dfrac{1}{p} + \dfrac{1}{q} = \dfrac{1}{f}$$p$ пов'язує відстань об'єкта від об'єктива і відстань зображення$q$ від об'єктива до$f$ фокусної відстані об'єктива.

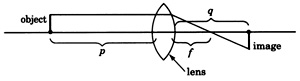
(a) Визначте фокусну відстань об'єктива, в якому об'єкт на відстані 10 футів створює зображення на відстані 6 футів.
(b) Визначте, наскільки далеко об'єкт знаходиться від об'єктива, якщо фокусна відстань об'єктива становить 6 дюймів, а відстань зображення - 10 дюймів.
(c) Визначте, наскільки далеко буде зображення від об'єктива з фокусною відстанню$4\dfrac{4}{5}$ см, а об'єкт знаходиться на відстані 12 см від об'єктива.

Відповідь

а)$f = \dfrac{15}{4}$ футів.

б)$p = 15$ дюймів.

в)$q = 8$ см.

Вправа$\PageIndex{28}$

Людина А може виконати завдання за 4 години, людина Б може виконати завдання за 6 годин, а людина С може виконати завдання за 3 години. Якщо всі три людини працюють разом, скільки часу знадобиться, щоб виконати завдання?

Вправа$\PageIndex{29}$

Три вхідні труби можуть заповнити накопичувальний бак за 4, 6 і 8 годин відповідно. Скільки часу займуть всі три труби, щоб заповнити бак?

Відповідь

$1\dfrac{11}{13}$годин

Вправа$\PageIndex{30}$

Впускний патрубок може заповнити бак за 10 годин. Бак має дві зливні труби, кожна з яких може спорожнити бак за 30 годин. Якщо всі три труби відкриті, чи можна заповнити бак? Якщо так, то скільки часу це займе?

Вправа$\PageIndex{31}$

Впускний патрубок може заповнити бак за 4 години. Бак має три зливні труби. Дві зливні труби можуть спорожнити бак за 12 годин, а третя може спорожнити бак за 20 годин. Якщо всі чотири труби відкриті, чи можна заповнити бак? Якщо так, то скільки часу це займе?

Відповідь

30 годин

Вправи для огляду

Вправа$\PageIndex{32}$

Фактор$12a^2 + 13a - 4$.

Вправа$\PageIndex{33}$

Знайти нахил лінії, що проходить через точки$(4, -3)$ і$(1, -6)$.

Відповідь

$m=1$

Вправа$\PageIndex{34}$

Знайдіть частку:$\dfrac{2 x^{2}-11 x-6}{x^{2}-2 x-24} \div \dfrac{2 x^{2}-3 x-2}{x^{2}+2 x-8}$

Вправа$\PageIndex{35}$

Знайдіть різницю:$\dfrac{x+2}{x^{2}+5 x+6}-\dfrac{x+1}{x^{2}+4 x+3}$

Відповідь

$0$

Вправа$\PageIndex{36}$

Розв'яжіть рівняння$\dfrac{9}{2m-5} = -2$