4.1.10: Застосування закону косинусів
- Page ID
- 54670
Відносини між трьома сторонами та кутом для непрямих трикутників.
Допомагаючи мамі спекти одного дня, ви двоє отримуєте незвичайну ідею. Ви хочете розрізати пиріг на шматочки, а потім заморозити по поверхні кожного шматочка. Ви починаєте з вирізання шматочка торта, але ви не зовсім правильно розрізаєте скибочку. Він закінчується косим трикутником, зі стороною 5 дюймів, стороною 6 дюймів та кутом\(70^{\circ} \) між сторонами, які ви виміряли. Чи можете ви допомогти мамі визначити довжину третьої сторони, щоб вона могла зрозуміти, скільки глазурі загасити?
Закон косинусів
Закон Косинуса є фантастичним продовженням теореми Піфагора до косих трикутників. У цьому розділі ми покажемо кілька цікавих способів використання цієї формули для аналізу реальних ситуацій.
Давайте розглянемо кілька проблем, де ми використовуємо Закон косинусів.
1. У грі в більярд гравець повинен покласти вісім м'яч в ліву нижню кишеню столу. В даний час вісім м'яч знаходиться на відстані 6.8 футів від нижньої лівої кишені. Однак через положення битка вона повинна відбити постріл з правого бокового бампера. Якщо вісім м'яч знаходиться на відстані 2,1 фута від місця на бампері їй потрібно вдарити і утворює\(168^{\circ} \) кут з кишенею і плямою на бампері, під яким кутом кулю потрібно залишити бампер?
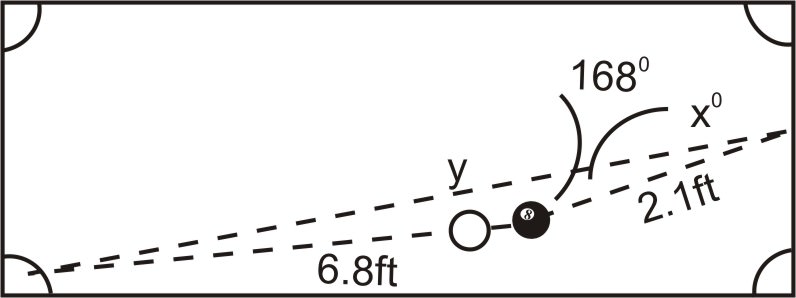
Примітка: Це насправді трюк постріл виконується обертанням вісім м'яч, і вісім м'яч насправді не буде подорожувати по прямих траєкторіях. Однак, щоб спростити задачу, припустимо, що вона рухається по прямих лініях.
У наведеному вище сценарії у нас є випадок SAS, а це означає, що нам потрібно використовувати Закон Косинусів, щоб розпочати вирішення цієї проблеми. Закон косинусів дозволить знайти відстань від плями на бампері до кишені (у). Як тільки ми дізнаємося y, ми можемо використовувати Закон Синеса, щоб знайти кут (X).
\(\begin{aligned} y^2 &=6.8^2+2.1^2−2(6.8)(2.1) \cos 168^{\circ} \\ y^2 &=78.59\\ y&=8.86 \text{ feet} \end{aligned}\)
2. Відстань від плями на бампері до кишені - 8,86 футів. Тепер ми можемо використовувати цю відстань і Закон синусів, щоб знайти кут X. Оскільки ми знаходимо кут, ми стикаємося з випадком SSA, що означає, що ми не могли б мати рішення, одне рішення або два рішення. Однак, оскільки ми знаємо всі три сторони, ця проблема дасть тільки одне рішення.
\ (\ почати {вирівняний}
\ dfrac {\ sin 168^ {\ circ}} {8.86} &=\ dfrac {\ sin X} {6.8}
\ dfrac {6.8\ sin 168^ {\ circ}} {8.86} &=\ sin X\\
0.1596 &\ приблизно\ гріх B\
\ кут B &8.77^ {circ}
\ end {вирівняний}\)
У попередньому прикладі ми розглянули, як ми можемо використовувати Закон Синеса та Закон Косинусів разом для вирішення проблеми, пов'язаної зі справою SSA. У цьому розділі ми розглянемо ситуації, коли ми можемо використовувати не тільки Закон Синуса і Закон Косинуса, а й теорему Піфагора і тригонометричні співвідношення. Ми також розглянемо ще одну реальну програму, що стосується справи SSA.
3. Троє вчених встановлюють обладнання для збору даних на місцевій горі. Відстань від готелю Person 2 до готелю Person 1 становить 13,5 метрів від готелю Person 3. Особа 1 розміщена за 72,6 метрів від гори. Гори утворюють\(103^{\circ} \) кут з особою 1 та особою 3, тоді як Особа 2 утворює\(92.7^{\circ} \) кут з особою 1 та особою 3. Знайдіть кут, утворений особою 3 з особою 1 та горою.
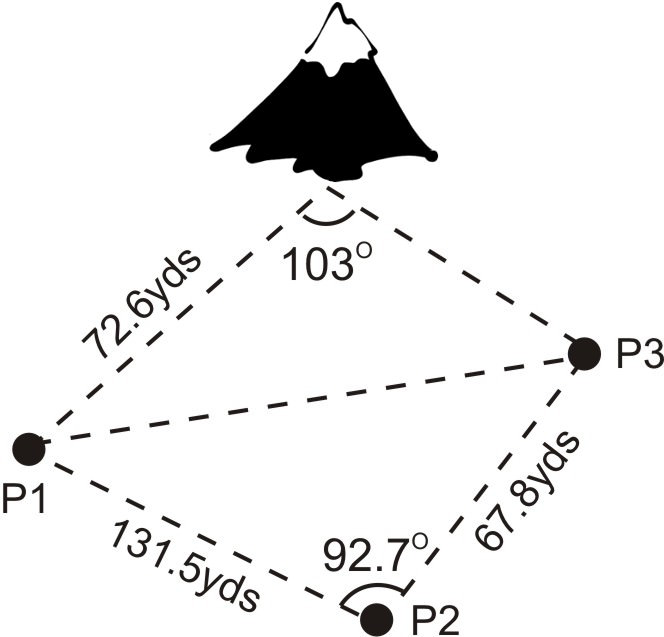
У трикутнику, утвореному трьома людьми, ми знаємо дві сторони і включений кут (SAS). Ми можемо використовувати Закон Косинусів, щоб знайти решту сторони цього трикутника, який ми будемо називати x, як тільки ми дізнаємося х, ми будемо дві сторони і не включений кут (SSA) в трикутнику, утвореному особою 1, особою 2, і горою. Потім ми зможемо використовувати Закон Синеса для обчислення кута, утвореного Людиною 3 з особою 1 та горою, яку ми будемо називати\(Y\).
Щоб знайти\(x\):
\(\begin{aligned} x^2 &=131.5^2+67.8^2−2(131.5)(67.8)\cos 92.7\\ x^2 &=22729.06397\\ x&=150.8 \text{ yds} \end{aligned}\)
Тепер, коли ми знаємо\(x=150.8\), ми можемо використовувати Закон Синеса, щоб знайти\(Y\). Оскільки це випадок SSA, нам потрібно перевірити, чи не матимемо у нас рішення, одного рішення чи двох рішень. Так як\(150.8>72.6\), ми знаємо, що у нас буде тільки одне рішення цієї проблеми.
\ (\ почати {вирівняний}
\ dfrac {\ sin 103} {150.8} &=\ dfrac {\ sin Y} {72.6}
\ dfrac {72.6\ sin 103} {
150.8} &=\ sin Y\\\\ sin Y\\\
28.0 &\ приблизно\ кут Y
\ кінець {вирівняний}\)
4. Кеті будує повітряний змій у формі трикутника.
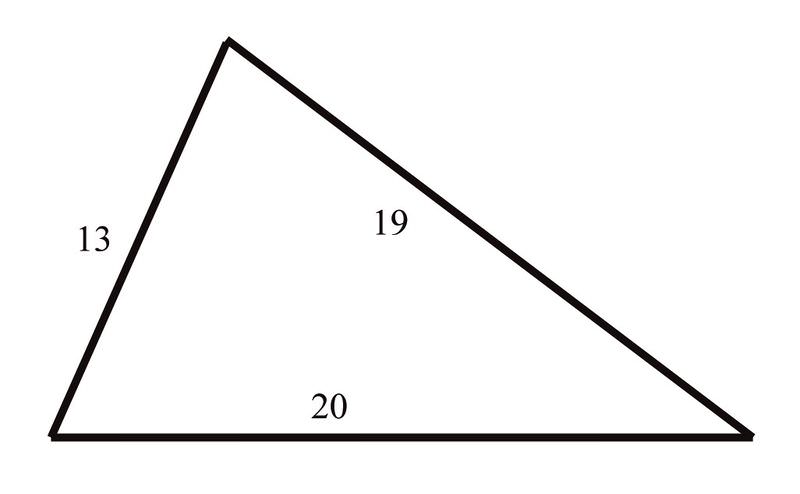
Вона знає, що довжини сторін a = 13 дюймів, b = 20 дюймів, а c = 19 дюймів. Яка міра кута між сторонами "\(a\)" і "\(b\)«?
Так як вона знає довжину кожної зі сторін трикутника, вона може скористатися Законом Косинусів, щоб знайти потрібний кут:
\ (\ почати {вирівняний}
c^ {2} &=a^ {2} +b^ {2} -2 (a) (b)\ cos C\\
19^ {2} &=13^ {2} +20^ {2} - (2) (13) (20) (20)\ cos C\\
361 &=169+400-520\ cos C\\ -208
=-520\ -208 = -520\ cos C
\\ cos C &= 0,4\\
C &\ приблизно 66,42^ {\ circ}
\ end {вирівняний}\)
Раніше вас просили визначити довжину третьої сторони.
Рішення
Ви можете використовувати Закон затишку, щоб допомогти мамі дізнатися довжину третьої сторони на шматку торта:
\ (\ почати {вирівняний}
c^ {2} &=a^ {2} +b^ {2} -2 a b\ cos С\\
c^ {2} &=5^ {2} +6^ {2} + (2) + (5) (6)\ cos 70^ {\ circ}\\
c^ {2} &=25+36+60 (.342)\\
c^ {2} &=81,52\\
c &\ приблизно 9.03
\ кінець {вирівняний}\)
Шматок пирога трохи більше 9 дюймів завдовжки.
Ви вирізаєте трикутник для школи, який виглядає так:
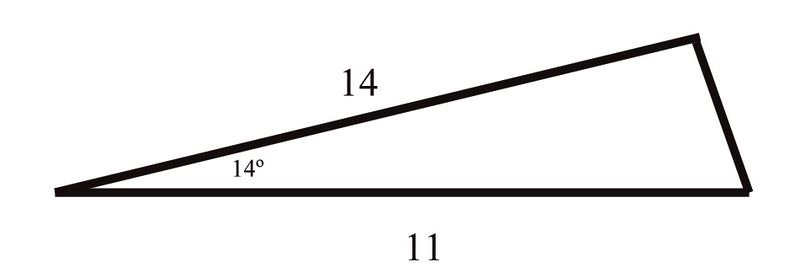
Знайдіть сторону\(c\) (яка є стороною, протилежною\(14^{\circ} \) куту) і\(\angle B \) (яка є кутом, протилежним стороні, яка має довжину 14).
Рішення
Ви знаєте, що дві сторони мають довжину 11 і 14 дюймів, і що кут між ними є\(14^{\circ} \). Ви можете скористатися цим, щоб знайти довжину третьої сторони:
\ (\ почати {вирівняний}
c^ {2} &=a^ {2} +b^ {2} -2 a b\ cos\ тета\\
c^ {2} &=121+196- (2) (11) (14) (.97)\\
c^ {2} &=121+196-307.384\
c^ {2} &=9.16\
c&3.03
\ end {вирівняний}\)
І за допомогою цього ви можете використовувати Закон Синеса для вирішення під невідомим кутом:
\ (\ почати {вирівняний}
\ dfrac {\ sin 14^ {\ circ}} {3.03} &=\ dfrac {\ sin B} {11}\
\ sin B&=\ dfrac {11\ sin 14^ {\ circ}} {3.03}
\\ sin B = 878\
B =\ sin ^ {-1} (.0307) =61.43^ {\ circ}
\ кінець {вирівняний}\)
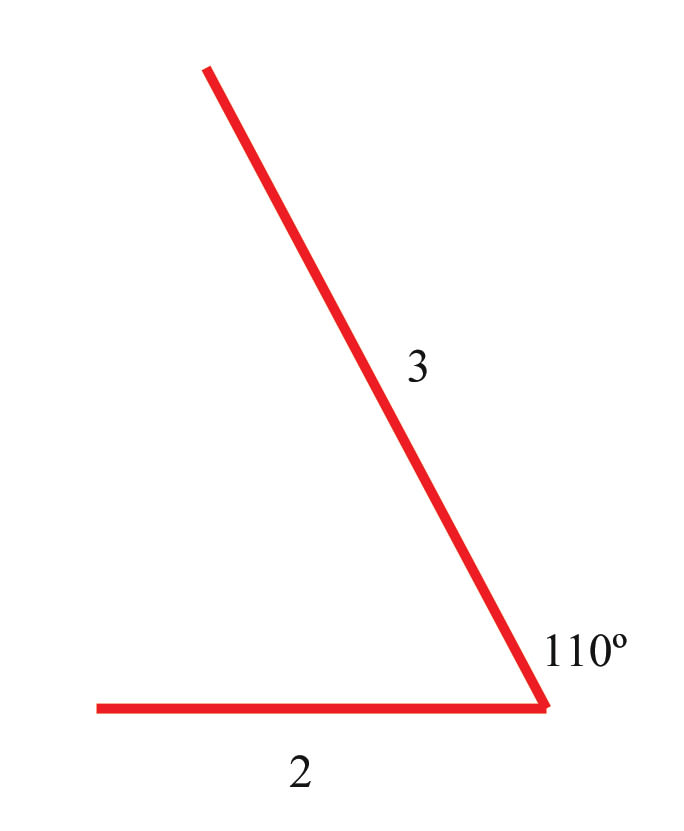
Під час піших прогулянок одного дня ви ходите 2 милі в одному напрямку. Потім ви\(110^{\circ} \) повертаєте ліворуч і пройдете ще 3 милі. Ваш шлях виглядає так:
Рішення
Коли ви знову повернетеся наліво, щоб завершити трикутник, який є вашим пішохідним шляхом протягом дня, як далеко вам доведеться пройти, щоб завершити третю сторону? Який кут слід повернути, перш ніж почати ходити додому?
Так як ви знаєте довжини двох ніжок трикутника, разом з кутом між ними, ви можете скористатися Законом Косинусів, щоб дізнатися, наскільки далеко вам доведеться пройти по третій ніжці:
\ (\ почати {вирівняний}
c^ {2} &=a^ {2} +b^ {2} +2 а б\ cos 70^ {\ circ}\\
c^ {2} &= 4+1+ (2) (2) (1) (.342)\\
c^ {2} &= 6.368\\
c&=\ sqrt {6.368}\ приблизно 2.52
\ кінець {вирівняний}\)
Тепер у вас є достатньо інформації, щоб вирішити внутрішній кут трикутника, який є додатковим до кута, який потрібно повернути:
\ (\ почати {вирівняний}
\ dfrac {\ sin A} {a} &=\ dfrac {\ sin B} {\ sin B}
\\ dfrac {\ sin 70^ {\ circ}} {\ dfrac {\ sin B} {2}\\ sin B}
\\ sin B =\ dfrac {2\ sin 70^ {\ circ}} {2.52} =\ dfrac {1.879} {2.52} =746\
B&=\ sin ^ {-1} (.746) =48,25^ {\ circ}
\ кінець { вирівняні}\)
Кут\(48.25^{\circ} \) - внутрішній кут трикутника. Так що перед початком будинку слід\(90^{\circ} +(90^{\circ} −48.25^{\circ} )=90^{\circ} +41.75^{\circ} =131.75^{\circ} \) повернути ліворуч.
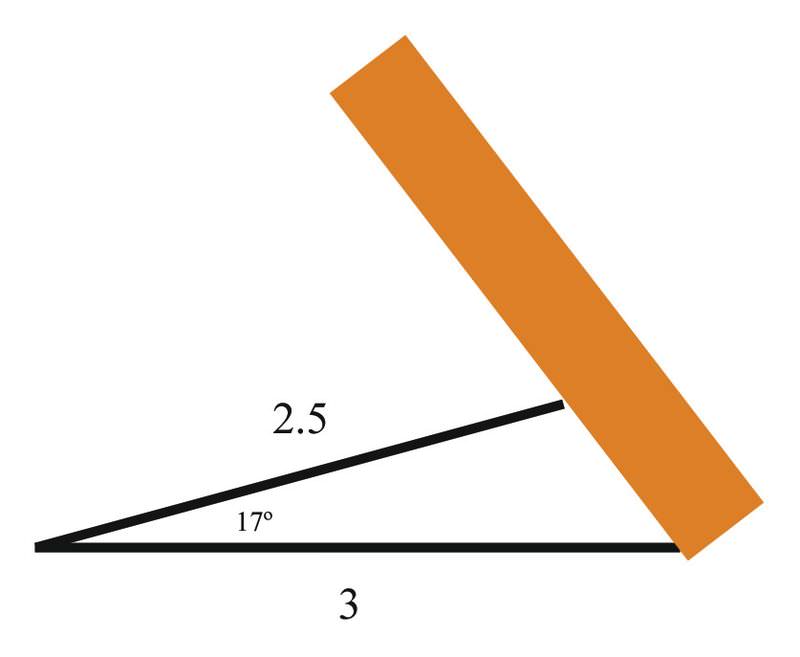
Опора на будівельному майданчику використовується для утримання дошки так, щоб вона складала трикутник, ось так:
Рішення
Якщо кут між опорою і землею є\(17^{\circ} \), довжина опори становить 2,5 метра, а відстань між тим, де дошка торкається землі і дном опори, становить 3 метри, як далеко вздовж дошки торкається опора? Який кут між дошкою і землею?
Спочатку слід використовувати Закон косинусів, щоб вирішити відстань від землі до місця, де опора зустрічається з дошкою:
\(\begin{aligned} c^2&=a^2+b^2+2ab \cos 17^{\circ} \\ c^2&=6.25+9+(2)(2.5)(3)\cos 17^{\circ} \\ c^2&=6.25+9+(2)(2.5)(3)(.956) \\ c^2&=26.722 \\ c&\approx 5.17 \end{aligned}\)
А тепер можна скористатися Законом Синеса:
\ (\ почати {вирівняний}
\ dfrac {\ sin A} {a} &=\ dfrac {\ sin B} {b}
\\ dfrac {\ sin 17^ {\ circ}} {\ dfrac {\ sin B} {2.5}\\
sin B &=\ dfrac {2.5\ sin 17^ {\ circ}} {5.17} =.1414\\
B&=\ sin ^ {-1} (.1414) =8.129^ {\ circ}
\ кінець {вирівняний}\)
Рецензія
В\(\Delta ABC\),\(a=12\),,\(b=15\), і\(c=20\).
- Знайти\(m\angle A\).
- Знайти\(m\angle B\).
- Знайти\(m\angle C\).
В\(\Delta DEF\),\(d=25\),,\(e=13\), і\(f=16\).
- Знайти\(m\angle D\).
- Знайти\(m\angle E\).
- Знайти\(m\angle F\).
В\(\Delta KBP\),\(k=19\),,\(\angle B=61^{\circ} \), і\(p=12\).
- Знайти довжину\(b\).
- Знайти\(m\angle K\).
- Знайти\(m\angle P\).
- Під час піших прогулянок одного дня ви йдете на 5 миль на схід, потім поверніть ліворуч і пройдіть ще 3 милі на\(30^{\circ} \) захід від півночі. У цей момент ви хочете повернутися додому. Як далеко ви від дому, якщо ви повинні були йти по прямій лінії?
- Паралелограм має сторони 20 і 31 фут, і кут\(46^{\circ} \). Знайти довжину більшої діагоналі паралелограма.
- Дірк хоче знайти довжину довгої будівлі від одного боку (точки\(A\)) до іншої (точки\(B\)). Він стоїть поза будівлею (в точці\(C\)), де він знаходиться на відстані 500 футів від точки\(A\) і 220 футів від точки\(B\). Кут при\(C\) є\(94^{\circ} \). Знайдіть довжину будівлі.
Визначити, чи можна кожен трикутник чи ні.
- \(a=12\),\(b=15\),\(c=10\)
- \(a=1\),\(b=5\),\(c=4\)
- \(\angle A=32^{\circ}\),\(a=8\),\(b=10\)
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 5.11.
Лексика
| Термін | Визначення |
|---|---|
| У комплекті Кут | Вхідний кут в трикутник - це кут між двома відомими сторонами. |
| закон косинусів | Закон косинусів - це правило, що стосується сторін трикутника з косинусом одного з його кутів. Закон косинусів говорить про те\(c^2=a^2+b^2−2ab\cos C\),\(C\) де кут поперек з боку\(c\). |
| SAS | SAS означає сторону, кут, сторону, і відноситься до того, що дві сторони і включений кут трикутника відомі. |
| ССС | SSS означає сторону, сторону, сторону і відноситься до того, що всі три сторони трикутника відомі в задачі. |
Додаткові ресурси
Відео: Розв'язування трикутників u\ sin g Закон Косинусів - Приклад 1
Практика: Застосування закону косинусів