2.5.8: Довжина хорди

Last updated
Save as PDF

Page ID: 54788

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Двічі радіус умножує синус половини кута в радіанах.

Вас попросили допомогти молодшим учням у вашій школі з класом фізичного виховання. Під час роботи одного дня вас просять взяти парашут, з яким студенти можуть грати. Коли студенти грають, один з них ходить через невелику частину парашута, а не під ним, як вона повинна. Якщо жолоб має форму кола з радіусом 6 метрів, а шлях, який студент пройшов через жолоб\(50^{\circ}\), покрив кут, яка довжина шляху вона пройшла через парашут?

Ви можете згадати з ваших досліджень геометрії, що акорд - це сегмент, який починається і закінчується на колі.

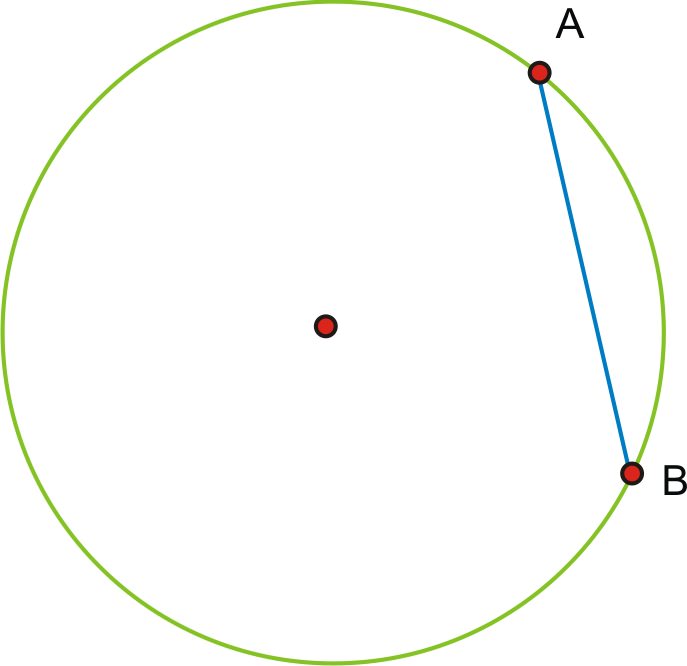
F-д_Ф 8631744 Е410526D47 де 89Е 731061872868809 FF84433АААААА0ЕЕЕ2+зображення_крихіткий+зображення_крихітка_крихітка_jpg — Малюнок\(\PageIndex{1}\)

\(\overline{AB}\)це акорд в колі.

Ми можемо обчислити довжину будь-якої хорди, якщо знаємо міру кута і довжину радіуса. Оскільки кожна кінцева точка хорди знаходиться на колі, відстань від центру до A та B збігається з довжиною радіуса.

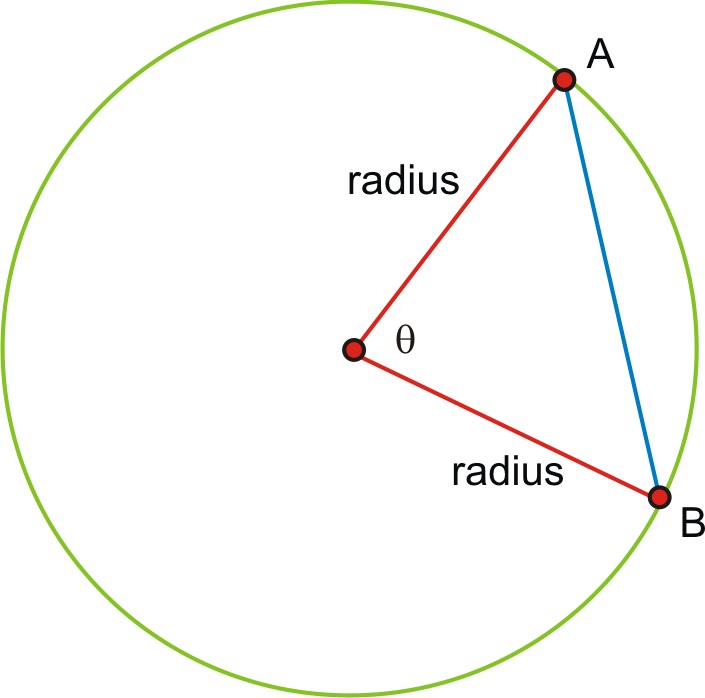
F-д_ФДА 746Е73385Е476Е8759Е 59Ф47Б461Д568к372А25943Д0Ф7С391566+зображення_крихіткий+зображення_крихіткий.jpg — Малюнок\(\PageIndex{2}\)

Далі, якщо ми розділимо кут, бісектриса кута повинна бути перпендикулярною хорді і бісекція його (ми залишимо доказ цього вашому класу Geometry). Це утворює прямокутний трикутник.

Ф-Д_7ЕС880А0626Б7724016Б64Д48825АДБ011Д5А327Е6АФФБ38С666662E518+зображення_крихіткий+зображення_крихіткий.jpg — Малюнок\(\PageIndex{3}\)

Тепер ми можемо використовувати просте синусоїдальне співвідношення, щоб знайти половину акорди, званої c тут, і подвоїти результат, щоб знайти довжину акорду.

\(\begin{aligned} \sin\dfrac{\theta}{2}&=\dfrac{c}{r} \\ c&=r\times \sin\dfrac{\theta}{2}\end{aligned}\)

Отже, довжина хорди дорівнює:

\(2c=2r \sin\dfrac{\theta}{2}\)

Пошук довжини акорду

1. Знайдіть довжину хорди кола радіусом 8 см і центральним кутом\(110^{\circ}\). Приблизний ваш відповідь до найближчого мм.

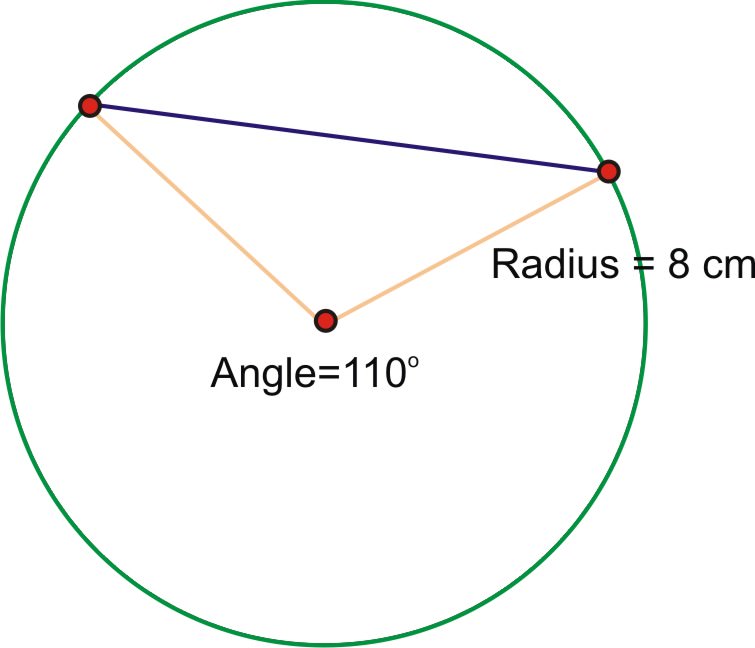
Ф-Д_59ФФ4ДФ Б27Ф31С1АЕ 41БКБК202ФА25867 БЕБ9АФ63А270Б108БА87+зображення_крихіткий+зображення_крихіткий.jpg — Малюнок\(\PageIndex{4}\)

Спочатку ми повинні перетворити кутову міру в радіани:

\(110\times \dfrac{\pi }{180}=\dfrac{11\pi }{18}\)

Використовуючи формулу, половина довжини хорди повинна дорівнювати радіусу кола, що дорівнює синусу половини кута.

\(\begin{aligned} \dfrac{11\pi }{18}\times \dfrac{1}{2}=\dfrac{11\pi }{36} \\ 8\times \sin \dfrac{11\pi }{36} \end{aligned}\)

Помножте цей результат на 2.

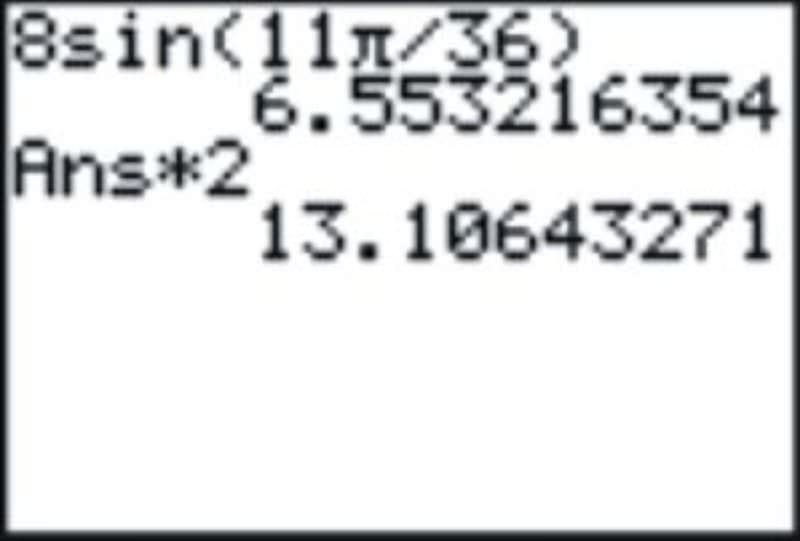
Ф-Д_4609 ФБД 627ФД7Ф04Б535Ф2БФ9Е2Б16159ЕАААААЕ4Б2072Ф03Б27А1+зображення_крихіткий+зображення_крихіткий.JPG — Малюнок\(\PageIndex{5}\)

Так, довжина хорди становить приблизно 13,1 см.

2. Знайти довжину хорди кола радіусом 2 м, що має центральний кут\(90^{\circ}\).

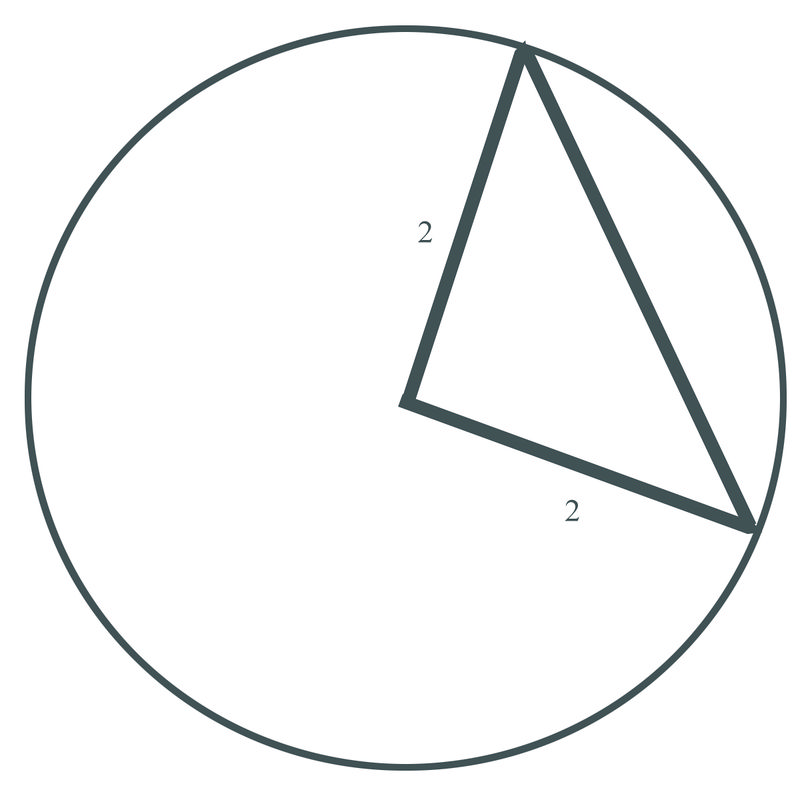
F-д_4Б604 плоский 55д921 ДДБ7473А77Е1132А51С9Ф448ФБ57А499ДДБД146+зображення_крихіткий+зображення_крихіткий.jpg — Малюнок\(\PageIndex{6}\)

Спочатку перетворіть кут в радіани:

\(90\times \dfrac{\pi }{180}=\dfrac{\pi }{2}\)

\(\dfrac{\pi }{2}\times \dfrac{1}{2}=\dfrac{\pi }{4} \\ 2\times \sin \dfrac{\pi }{4}\)

Помножте цей результат на 2.

Таким чином, відповідь становить приблизно 2,83 метра.

3. Знайти довжину хорди кола радіусом 1 м і центральним кутом\(170^{\circ}\).

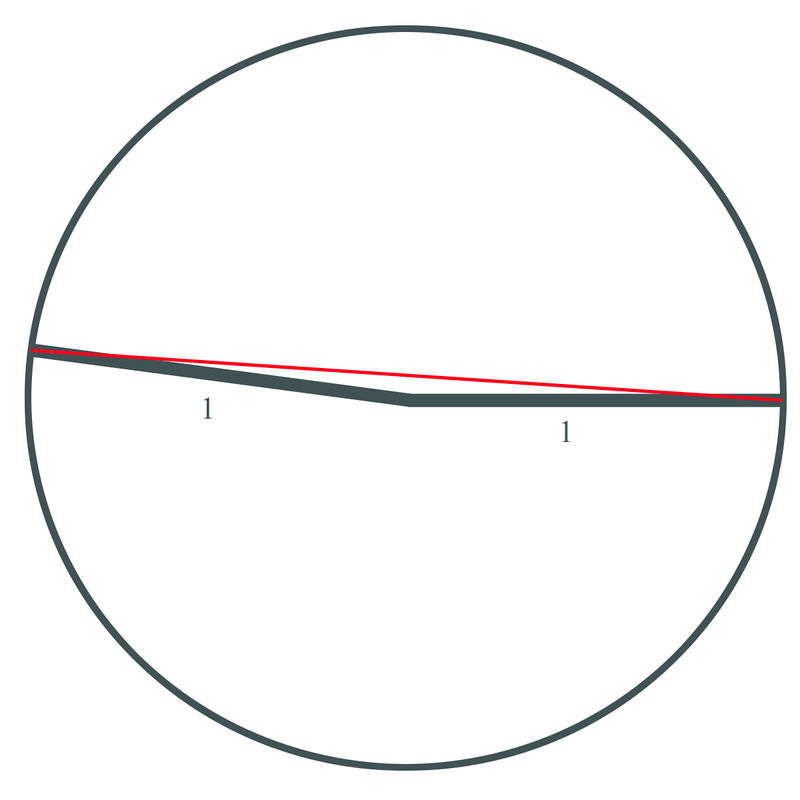
Ф-Д_Б3ДФ 05А 8Е24624Ф85А25579Е660Д41845Е4ДБКБС5А5Ф8838А6Ф5Д74+зображення_крихіткий+зображення_крихіткий.jpg — Малюнок\(\PageIndex{7}\)

Спочатку ми повинні перетворити кутову міру в радіани:

\(170\times \dfrac{\pi }{180}=\dfrac{17\pi }{18}\)

\(\begin{aligned} \dfrac{17\pi }{18} \times \dfrac{1}{2}&= \dfrac{17\pi }{36} \\1\times \sin \dfrac{17\pi }{36}&=.996\end{aligned}\)

Помножте цей результат на 2.

Отже, довжина дуги приблизно дорівнює 1,992

Зверніть увагу, що довжина хорди становить майже 2 метри, що було б діаметром кола. Якби кут був 180 градусів, хорда була б просто відстань по всьому колу, що проходить через середину, яка є діаметром.

Приклад\(\PageIndex{1}\)

Раніше вас запитали, яка довжина шляху вона пройшла через парашут.

Рішення

За допомогою рівняння довжини хорди в руці можна обчислити відстань, яку студент пробіг через парашут:

Спочатку перетворіть міру в градусах в радіани:

\(50\times \dfrac{\pi }{180} \approx .27\pi\)

\(2r \sin \dfrac{\theta}{2}=(2)(6)\sin \dfrac{.27\pi }{2}=12 \sin.135\pi \approx 4.94 \text{ meters}\)

Приклад\(\PageIndex{2}\)

Якщо ви запускаєте шматок струни через пончик, який ви їсте, і радіус між кінцевими точками струни до центру пончика становить 4 дюйми, як довго це рядок, якщо кут змітається акордом\(20^{\circ}\)?

Рішення

Ви можете використовувати рівняння\(C=2r\sin\left(\dfrac{\theta}{2}\right)\) для вирішення цієї проблеми: (Не забудьте перетворити кути в радіани)

\(\begin{aligned} C&=2r\sin \left(\dfrac{\theta}{2}\right) \\ C&=(2)(4)\sin\left(\dfrac{.349}{2}\right) \\ C&=8(.1736) \\ C&=1.388 \text{ inches}\end{aligned}\)

Приклад\(\PageIndex{3}\)

Ви їсте вечерю одну ніч з сім'єю в місцевому італійському ресторані. Шматок спагетті робить акорд по всій вашій тарілці. Ви знаєте, що довжина пасма спагетті становить 5 дюймів, а радіус пластини - 7 дюймів. Який кут змітає акорд?

Рішення

Так як радіус пластини і довжина хорди відомі, можна вирішити для кута:

\ (\ почати {вирівняний}
C & = 2 r\ sin\ ліворуч (\ dfrac {\ тета} {2}\ вправо)\
\ dfrac {C} {2 r} &=\ sin\ ліворуч (\ dfrac {\ тета} {2}\ справа)\\ sin ^ {-1}
\ ліво (\ dfrac {c} {2 r}\ праворуч) &=\ dfrac {c} {2 r}\ праворуч) &=\ dфракція {\ тета} {2}
\\ sin ^ {-1}\ ліворуч (\ dfrac {5} {14}\ праворуч) &=\ dfrac {\ тета} {2}\\
.365&=\ dfrac {\ тета} {2}\
\ тета&=.73
\ кінець {вирівняний}\)

Кут, що охоплюється спагетті, становить 0,73 радіана.

Приклад\(\PageIndex{4}\)

Якщо ви намалюєте акорд по колу і зробите акорд поперек нього, який має довжину 15 дюймів, змітаючи кут\(\pi \) радіанів, який радіус кола ви намалювали?

Рішення

Використовуючи рівняння для довжини хорди:

\(\begin{aligned} c&=2r \sin(\dfrac{\theta }{2}) \\ 15&=(2r)\sin(\dfrac{\pi }{2}) \\ r&=7.5 \end{aligned}\)

Як бачите, радіус кола дорівнює 7,5 дюймів. Це те, що слід очікувати, так як акорд змітає кут\(\pi \). Це означає, що він змітає половину кола, так що хорда фактично йде по всьому діаметру кола. Так якщо хорда йде по діаметру і має довжину 15 дюймів, то радіус кола повинен бути 7,5 дюймів.

Рецензія

Знайти довжину хорди кола радіусом 1 м і центральним кутом\(100^{\circ}\).
Знайти довжину хорди кола радіусом 8 км і центральним кутом\(130^{\circ}\).
Знайти довжину хорди кола з радіусом 4 в і центральним кутом\(45^{\circ}\).
Знайти довжину хорди кола з радіусом 3 фути і центральним кутом\(32^{\circ}\).
Знайдіть довжину хорди кола радіусом 2 см і центральним кутом\(112^{\circ}\).
Знайти довжину хорди кола з радіусом 7 в і центральним кутом\(135^{\circ}\).

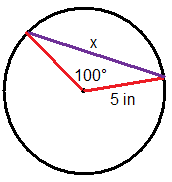
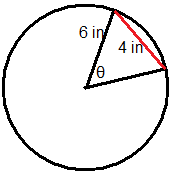
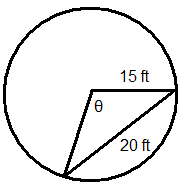
Вирішіть для відсутньої змінної в кожному колі.

Малюнок\(\PageIndex{8}\)
Малюнок\(\PageIndex{9}\)
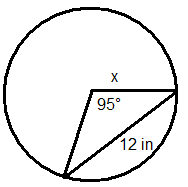
Малюнок\(\PageIndex{10}\)
Малюнок\(\PageIndex{11}\)
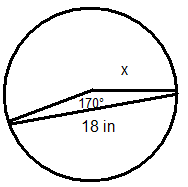
Малюнок\(\PageIndex{12}\)
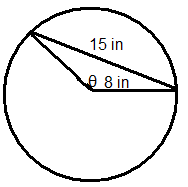
Малюнок\(\PageIndex{13}\)

Використовуйте картинку нижче для питань 13-15.

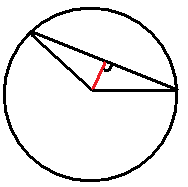
F-D_2A1F103878 CDD34C55CA9A6AC 67111db94d330d2FBAE68C2344F9+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{13}\)

Припустимо, ви знали довжину хорди, довжину радіуса і центральний кут вищевказаного кола. Опишіть один із способів знайти довжину червоного відрізка за допомогою теореми Піфагора.
Припустимо, ви знали довжину хорди, довжину радіуса і центральний кут вищевказаного кола. Опишіть один із способів знайти довжину червоного відрізка за допомогою косинуса.
Що потрібно знати для того, щоб знайти площу відрізка (ділянку кола між хордою і краєм кола)? Опишіть, як знайти площу цього регіону.

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 2.7.

Лексика

Термін	Визначення
Акорд	Хорда - це пряма лінія по колу, що перетинає коло в двох місцях, але не проходить через центр кола.

Додаткові ресурси

Інтерактивний елемент

Відео: Акорди

Практика: Довжина акорду