Skip to main content
LibreTexts - Ukrayinska

2.5.7: Площа сектора

  1. Last updated
  2. Save as PDF
  • Page ID
    54778

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Половина радіуса в квадраті разів дорівнює куту в радіанах.

    Під час обіду з друзями одного дня ви вирішите отримати пиріг. У шкільній їдальні продається пироги, якщо ви купуєте весь пиріг замість окремого скибочки. Так як ви і ваші друзі плануєте з'їсти весь пиріг в будь-якому випадку, ви із задоволенням зробите покупку.

    Ви вирішите відрізати собі шматочок. Коли ви вийняли свій розділ пирога, один з ваших друзів заперечує, що ви вирізали більше, ніж ваша справедлива частка. Якщо радіус пирога шість дюймів, а кут, утворений кінцем клина пирога\(30^{\circ}\), є, яка площа вашого пирога шматок? Це більше, ніж ваша справедлива частка, якщо є п'ять людей (включаючи вас), що розділяють пиріг?

    Площа сектору

    Однією з найпоширеніших геометричних формул є площа кола:

    \(A=\pi r^2\)

    У плані кутового повороту це площа, створена\(2\pi \) радіанами.

    \(2\pi \text{ rad}=\pi r^2 \text{ area}\)

    Половина кола, або\(\pi \) радіанове обертання створить переріз, або сектор кола, рівний половині площі або:

    \(\dfrac{1}{2} \pi r^2\)

    Таким чином, кут 1 радіан буде визначати площу сектора, рівну:

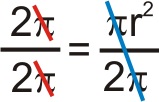
    Ф-Д_С1Ф180А718БК 6413 ФЕ766А 5319 ЕЕК ліжко 440С3ФЧ1Ф87ДД53ЕБ10963E+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{1}\)

    \(1=\dfrac{1}{2}r^2\)

    З цього ми можемо визначити площу сектора, створеного будь-яким кутом,\(\theta \) радіанами, бути:

    \(A=\dfrac{1}{2}r^2\theta\)

    Знаходження району

    1. Культури часто вирощують за допомогою техніки, яка називається центровим зрошенням, що призводить до кругової форми полів.

    F-D517963F0614E487E44FE982CEB92 BCCA593312083CE29220D10F9+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_jpg
    Малюнок\(\PageIndex{2}\)

    Ось супутниковий знімок, зроблений над полями в Канзасі, які використовують цей тип зрошувальної системи.

    F-D_475594C8F1D40081294EF2242B5909906818FE15C13D9DCCE231BC76+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_jpg
    Малюнок\(\PageIndex{3}\)

    Якщо зрошувальна труба довжиною 450 м, якою площею можна зрошувати після обертання\(\dfrac{2\pi }{3}\) радіанів?

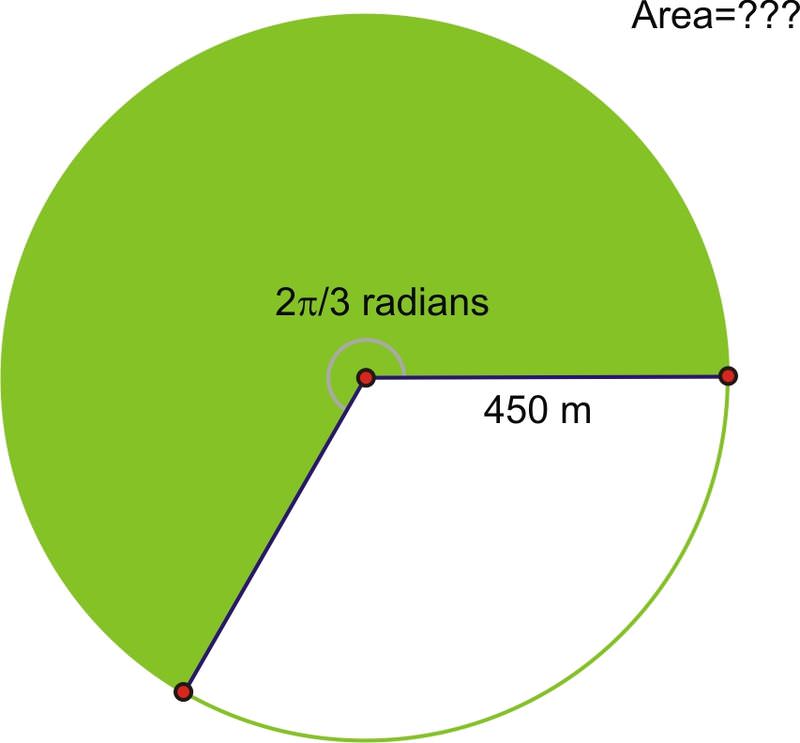
    Ф-Д_71 ДБ15048270833568 ДКС7ФФ ФА848Ф04С773Ф5ФА7С10ЕДБ127КДФ7Ф7Ф8+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{4}\)

    Використовуючи формулу:

    \(\begin{aligned} A&=\dfrac{1}{2}r^2\theta \\ A&=\dfrac{1}{2}(450)^2\left(\dfrac{2\pi }{3}\right)\end{aligned}\)

    Ф-Д_556870750А89846БД6Д3157Е00Б40734864Ф55ДБ1ФК25Е300Б3БАЕ0С+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{5}\)

    Площа становить приблизно 212 058 квадратних метрів.

    2. У пончика посередині отвір радіусом 1 см, а відстань від центру отвору до зовнішнього краю пончика - 3 см. Яка площа сектора 14 пончика?

    Ф-Д_2А73218 АФК 3Е2С2226ДФ 79CDB88768369204Д5Е07Б415Д409026ФД75+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{6}\)

    Формула для площі сектора є\(A=\dfrac{1}{2}r^2\theta \). За допомогою цієї формули знайти площу сектора від центру назовні дає:

    \(\begin{aligned} A &=\dfrac{1}{2}r^2 \theta \\ A &=\dfrac{1}{2}3^2 \dfrac{\pi }{2}\\ A&=\dfrac{9\pi }{4} \end{aligned}\)

    Тепер необхідно відняти площу сектора, який є частиною отвору, а значить, не частиною пончика:

    \(\begin{aligned} A &= \dfrac{1}{2}r^2 \theta \\ A &=\dfrac{1}{2} (1)^2 \dfrac{\pi }{2}\\ A&=\pi 4 \end{aligned}\)

    Площа сектора пончиків:\(A=\dfrac{9\pi }{4}−\dfrac{\pi }{4}=\dfrac{8\pi }{4}=2\pi\)

    3. Водій подорожує круговою доріжкою, яка має радіус дії 70 метрів. Якщо кут від стартової лінії до її поточної позиції дорівнює\(\dfrac{\pi }{3}\) радіанам, яка площа сектора простежується її автомобілем?

    Ф-Д_74АД 32С39455078058 АДБА 23574644 КБ4557А2А14Е899 Е7Е9Е22+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{7}\)

    Площа сектору становить:\(A=\dfrac{1}{2}r^2\theta \). Це призводить нас до:

    \(\begin{aligned} A &=\dfrac{1}{2}r^2\theta \\ A &=\dfrac{1}{2}(70)^2 \dfrac{\pi }{3}\\ A&\approx 73.3 \text{ meters} \end{aligned}\)

    Приклад\(\PageIndex{1}\)

    Раніше вас запитали, яка площа вашого шматка пирога.

    Рішення

    Тепер ви знаєте, що рівняння для площі кола, зметеного деяким кутом, таке:

    \(A=\dfrac{1}{2}r^2\theta\)

    Застосовуючи це до шматочка пирога, у вас є область:

    \(A=\dfrac{1}{2}\times 62\times \dfrac{\pi }{6}=3\pi \)

    А загальна площа пирога становить:

    \(\pi r^2=36\pi\)

    Щоб дізнатися, яка ваша справедлива порція пирога, помножте загальну площу на вашу дріб:

    \(\dfrac{1}{5} \times 36\pi =7.2\pi\)

    А оскільки шматок, який ви взяли, має розмір лише 3\ pi, ви точно не берете занадто багато!

    Приклад\(\PageIndex{2}\)

    Якщо радіус сектора становить 5 футів, а сектор змітає кут\(43^{\circ}\), знайдіть область сектора.

    Рішення

    Оскільки ви це знаєте\(A=\dfrac{1}{2}r^2\theta \), ви можете вирішити для області (не забудьте перетворити градуси кута в радіани):

    \(\begin{aligned} A&=\dfrac{1}{2}r^2\theta \\ A&=\dfrac{1}{2} (25)(.75) \\ A&=9.375 \end{aligned}\)

    Приклад\(\PageIndex{3}\)

    Якщо пиріг клин має площу 15 квадратних дюймів, а пиріг має радіус 9 дюймів, знайдіть кут, змітається сектором.

    Рішення

    Оскільки ви це знаєте\(A=\dfrac{1}{2}r^2\theta \), ви можете вирішити для кута, змітається сектором (не забувайте, що кут буде вимірюватися в радіанах):

    \(\begin{aligned} A&=\dfrac{1}{2}r^2\theta \\ 15&=\dfrac{1}{2} (81)(\theta ) \\ \theta &=\dfrac{(2)(15)}{81} \\ \theta &=.37 \end{aligned}\)

    Приклад\(\PageIndex{4}\)

    Якщо у вас є шматок круглого торта, який має площу 20 квадратних дюймів, і ви знаєте, що шматок змітає кут\(25^{\circ}\), знайдіть радіус торта.

    Рішення

    Оскільки ви це знаєте\(A=\dfrac{1}{2}r^2\theta \), ви можете вирішити для радіуса пирога (не забудьте перетворити градуси кута в радіани):

    \(\begin{aligned} A&=\dfrac{1}{2}r^2\theta \\ 20&=\dfrac{1}{2}(r^2)(.436) \\ r^2&=\dfrac{(2)(20)}{.436 }\\ r^2&=91.743 \\ r&=9.58 \end{aligned}\)

    Рецензія

    1. Якщо радіус сектора становить 8 дюймів, а центральний кут сектора -\(40^{\circ}\), знайдіть площу сектора.
    2. Якщо радіус сектора становить 12 дюймів, а центральний кут сектора -\(\dfrac{\pi }{6}\) радіани, знайдіть площу сектора.
    3. Якщо радіус сектора становить 6 дюймів, а центральний кут сектора -\(140^{\circ}\), знайдіть площу сектора.
    4. Якщо радіус сектора становить 5 дюймів, а центральний кут сектора -\(\dfrac{5\pi }{3}\) радіани, знайдіть площу сектора.
    5. Якщо радіус сектора становить 10 дюймів, а центральний кут сектора -\(100^{\circ}\), знайдіть площу сектора.
    6. Якщо пиріг клин має площу 10 квадратних дюймів, а пиріг має радіус 6 дюймів, знайдіть кут, змітається сектором.
    7. Якщо пиріг клин має площу 15 квадратних дюймів, а пиріг має радіус 4 дюйми, знайдіть кут, змітається сектором.
    8. Якщо пиріг клин має площу 12 квадратних дюймів, а пиріг має радіус 3 дюйми, знайдіть кут, змітається сектором.
    9. Якщо у вас є шматок круглого торта, який має площу 20 квадратних дюймів, і ви знаєте, що шматок змітає кут\(\dfrac{\pi }{3}\) радіанів, знайдіть радіус пирога.
    10. Якщо у вас є шматок круглого пирога, який має площу 100 квадратних дюймів, і ви знаєте, що шматок змітає кут\(50^{\circ}\), знайти радіус торта.
    11. Якщо у вас є шматок круглого пирога, який має площу 35 квадратних дюймів, і ви знаєте, що шматок змітає кут\(\dfrac{2\pi }{5}\) радіанів, знайдіть радіус пирога.
    12. Якщо у вас є шматок круглого торта, який має площу 20 квадратних дюймів, і ви знаєте, що шматок змітає кут\(30^{\circ}\), знайдіть радіус торта.

    Піца має радіус 10 в. Використовуйте цю інформацію, щоб відповісти на питання 13-15.

    1. Зріз видаляється. Довжина скоринки відсутнього скибочки становить 3 дюйма. Яка площа відсутнього зрізу?
    2. Ви їсте три штуки з центральним кутом\(\dfrac{4\pi }{5}\). Яку площу піци ви їли?
    3. Велика піца має радіус дії 12 дюймів. Яка площа половини великої піци?

    Огляд (Відповіді)

    Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 2.6.

    Лексика

    Термін Визначення
    Сектор Сектор кола - це частина кола, що міститься між двома радіусами кола. Сектори можна вимірювати в градусах.

    Додаткові ресурси

    Відео: Довжина дуги і площа сектора

    Практика: Область сектору