2.1.2: Функції трига калькулятора

Тригонометричні співвідношення на основі сторін прямокутних трикутників по відношенню до кута.

Тригонометричні коефіцієнти з калькулятором

Існує фіксоване значення синуса, косинуса та тангенса для кожного кута, від$0^{\circ}$ до$90^{\circ}$. Ваш науковий (або графічний) калькулятор знає всі тригонометричні значення для будь-якого кута. Ваш калькулятор повинен мати кнопки [SIN], [COS] та [TAN]. Ви можете скористатися калькулятором і тригонометричними співвідношеннями, щоб знайти відсутні сторони прямокутного трикутника, встановивши рівняння трига.

Що робити, якщо вам дали трикутник 20-70-90? Як ви могли знайти синус, косинус і тангенс$70^{\circ}$ кутів$20^{\circ}$ і?

Приклад$\PageIndex{1}$

Знайдіть довжину відсутніх сторін і округляйте свої відповіді до найближчої десятої:

Малюнок$\PageIndex{1}$

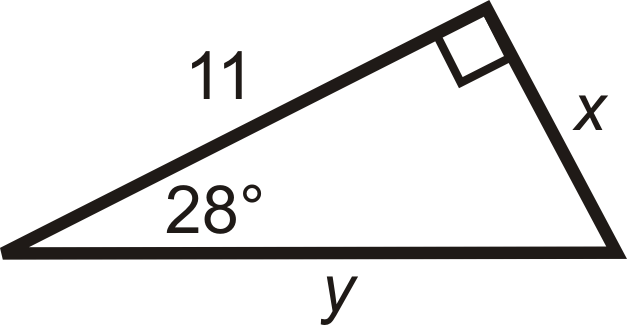
Рішення

Використовуйте тангенс for$x$ і косинус для$y$.

\ (\ почати {масив} {rlrl}
\ тан 28^ {\ circ} & =\ dfrac {x} {11} &\ cos 28^ {\ circ} & =\ dfrac {11} {\
cdot\ tan 28^ {\ circ} & = x &\ dfrac {11} {\ cos 28^ {\ circ} =y\\
x &\ приблизно 5.8 & y &\ приблизно 12.5
\ кінець {масив}\)

Приклад$\PageIndex{2}$

Знайдіть довжину відсутніх сторін і округляйте свої відповіді до найближчої десятої:

Малюнок$\PageIndex{2}$

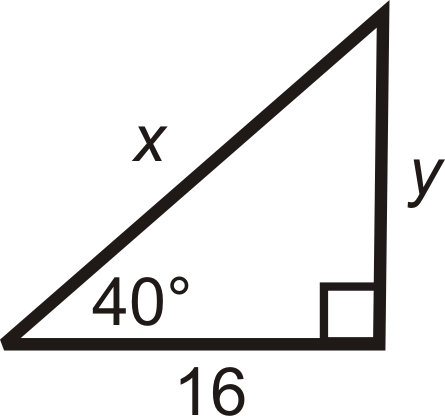
Рішення

Використовуйте тангенс for$y$ і косинус для$x$.

\ (\ почати {вирівняний}
\ тан 40^ {\ circ} &=\ dfrac {y} {16} &\ cos 40^ {\ circ} &=\ dfrac {16} {\
cdot\ tan 40^ {\ circ} &= y &\ dfrac {16} {\ cos 40^ {\ circ}} &x\
y &\ приблизно 13.4 &\ quad x &\ приблизно 20.9
\ кінець {вирівняний}\)

Приклад$\PageIndex{3}$

Знайдіть тригонометричні значення, скориставшись вашим калькулятором:

$sin 78^{\circ}$,$\cos 60^{\circ}$,$\tan 15^{\circ}$

Рішення

Округлення до 4 знаків після коми.

Залежно від вашого калькулятора, ви вводите ступінь, а потім натисніть кнопку трига або навпаки. Крім того, переконайтеся, що режим вашого калькулятора знаходиться в ГРАДУСАХ.

$\begin{aligned} \sin 78^{\circ}&=0.97815 \\ \cos 60^{\circ}&=0.5 \\ \tan 15^{\circ}&=0.26795\end{aligned}$

Приклад$\PageIndex{4}$

Знайдіть значення кожної змінної. Округлите відповідь до найближчої десятої.

Малюнок$\PageIndex{3}$

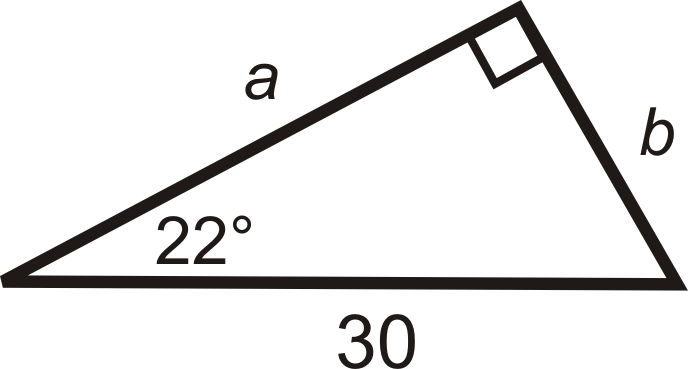
Рішення

Нам дано гіпотенузу. Використовуйте синус для пошуку$b$ та косинус для пошуку$a$. Використовуйте калькулятор, щоб оцінити синус і косинус кутів.

Малюнок$\PageIndex{4}$

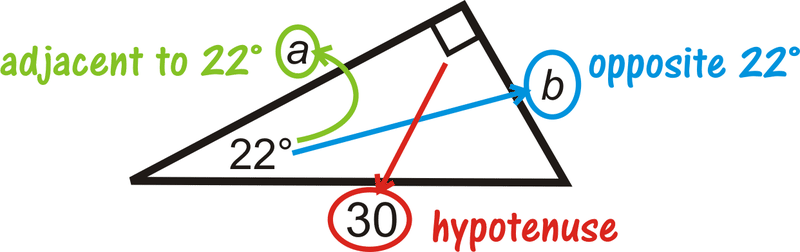
\ (\ почати {масив} {rlrl}
\ sin 22^ {\ circ} & =\ dfrac {b} {30} &\ cos 22^ {\ circ} & =\ dfrac {a} {
30}\ cdot\ sin 22^ {\ circ} & = {\ circ} & =\\
b\\ приблизно 11.2 & a\ приблизно 27,8
\ кінець {масив}\)

Приклад$\PageIndex{5}$

Знайдіть значення кожної змінної. Округлите відповідь до найближчої десятої.

Рішення

Малюнок$\PageIndex{5}$

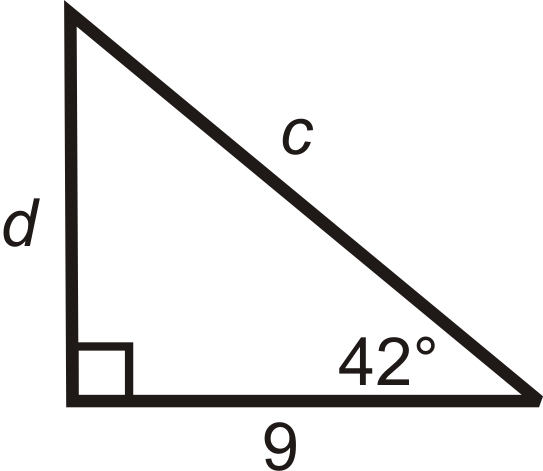
Нам дається прилегла ніжка до$42^{\circ}$. Щоб знайти$c$, використовуйте косинус і використовуйте тангенс, щоб знайти$d$.

\ (\ почати {масив} {rlrl}
\ cos 42^ {\ circ} & =\ dfrac {a d j a c e n t} {\ текст {гіпотенуза}} =\ dfrac {9} {c} &\ tan 42^ {\ circ} & =\ dfrac {\ текст {навпроти}} {\ текст {суміжний}} =\ dfrac {d} 9}\
c\ cdot\ cos 42^ {\ коло} & = 9 & 9\ cdot\ tan 42^ {\ circ} & = д\\
c & підсилювач; =\ dfrac {9} {\ cos 42^ {\ circ}}\ приблизно 12.1 & d\ приблизно 27,0
\ кінець {масив}\)

Кожен раз, коли ви використовуєте тригонометричні співвідношення, використовуйте тільки ту інформацію, яку вам дають. Це призведе до отримання найбільш точних відповідей.

Рецензія

Скористайтеся калькулятором, щоб знайти значення кожної функції трига нижче. Округлення до чотирьох знаків після коми.

1. $\sin 24^{\circ}$
2. $\cos 45^{\circ}$
3. $\tan 88^{\circ}$
4. $\sin 43^{\circ}$
5. $\tan 12^{\circ}$
6. $\cos 79^{\circ}$
7. $\sin 82^{\circ}$

Знайдіть довжину відсутніх сторін. Округляйте свої відповіді до найближчої десятої.

8. 
   

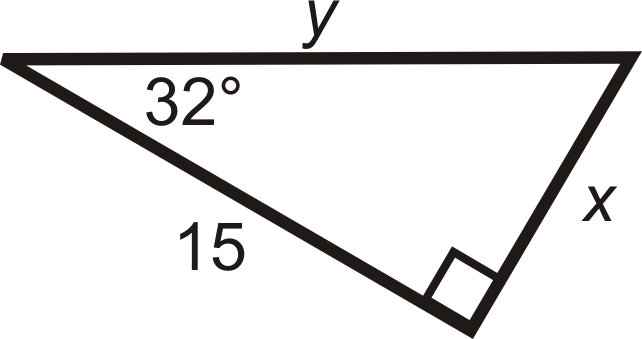
   Малюнок$\PageIndex{6}$

9. 

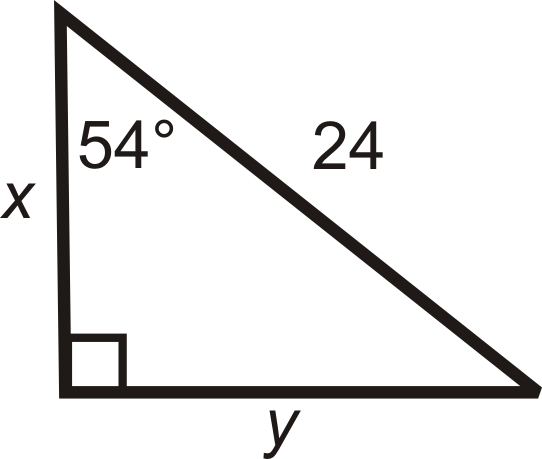
   Малюнок$\PageIndex{7}$

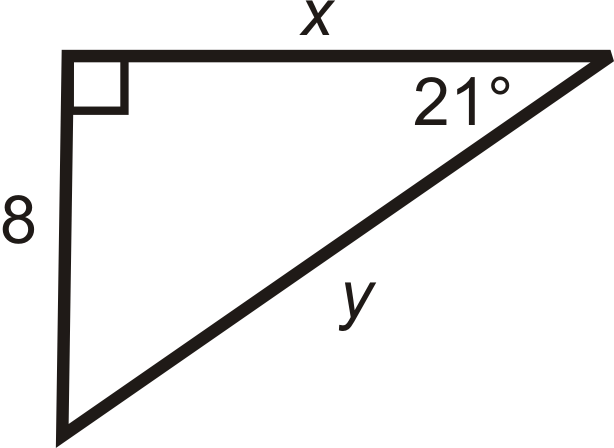10. Малюнок\(\PageIndex{8}\)

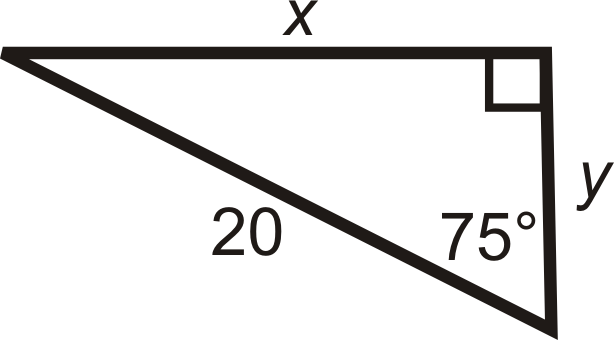11. Малюнок\(\PageIndex{9}\)

Огляд (Відповіді)

Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 8.8.

Ресурси

Лексика

Термін	Визначення
тригонометрія	Вивчення взаємозв'язків сторін і кутів прямих трикутників.
Гіпотенуза	Гіпотенуза прямокутного трикутника - найдовша сторона прямокутного трикутника. Вона знаходиться поперек від прямого кута.
Ніжки прямокутного трикутника	Ніжки прямокутного трикутника - це дві коротші сторони прямокутного трикутника. Ноги примикають до прямого кута.
Тригонометричні коефіцієнти	Співвідношення, які допомагають нам зрозуміти відносини між сторонами і кутами прямих трикутників.

Додаткові ресурси

Інтерактивний елемент

Відео: Вступ до тригонометричних функцій з використанням трикутників

Діяльність: Тригонометричні коефіцієнти з калькулятором Питання обговорення

Практика: Функції трига калькулятора

Реальний світ: Тангенс синусосинуса