2.1.6: ЗАГАР

Last updated
Save as PDF

Page ID: 54634

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Дослідіть співвідношення тангенсів і використовуйте його, щоб знайти відсутні сторони правильних трикутників.

Коли міра кута збільшується між\(0^{\circ}\) і\(90^{\circ}\), як змінюється дотичне відношення кута?

Коефіцієнт дотичної

Нагадаємо, що один із способів показати, що два трикутники схожі, - це показати, що вони мають дві пари конгруентних кутів. Це означає, що два правильних трикутника будуть схожі, якщо вони мають одну пару конгруентних непрямих кутів.

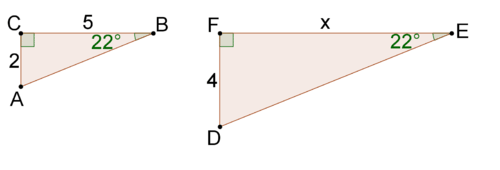
Два правильних трикутника вище схожі, оскільки вони мають дві пари конгруентних кутів. Це означає, що відповідні їм сторони пропорційні. \(\overline{DF}\)і\(\overline{AC}\) є відповідними сторонами, оскільки вони обидва протилежні\(22^{\circ}\) куту. \(\dfrac{DF}{AC}=\dfrac{4}{2}=2\), Таким чином, коефіцієнт масштабу між двома трикутниками дорівнює 2. Це означає\(x=10\), що, тому що\(\dfrac{FE}{CB}=\dfrac{10}{5}=2\).

Співвідношення між двома ніжками будь-якого\(22^{\circ}\) прямокутного трикутника завжди буде однаковим, тому що всі\(22^{\circ}\) правильні трикутники схожі. Ставлення довжини ноги, протилежної\(22^{\circ}\) куту, до довжини ноги, прилеглої до\(22^{\circ}\) кута, складе\(\dfrac{2}{5}=0.4\). Ви можете використовувати цей факт, щоб знайти відсутню сторону іншого\(22^{\circ}\) прямокутного трикутника.

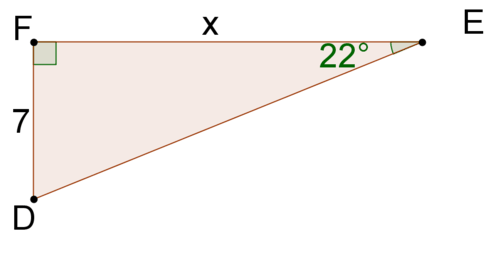
Тому що це\(22^{\circ}\) прямокутний трикутник, ви це знаєте\(\dfrac{\text{opposite leg}}{\text{adjacent leg}}=\dfrac{2}{5}=0.4\).

\(\begin{aligned} \dfrac{\text{opposite leg}}{\text{adjacent leg}}&=0.4 \\ \dfrac{7}{x}&=0.4 \\ 0.4x &=7\\ x&=17.5 \end{aligned}\)

Співвідношення між протилежною ніжкою і сусіднім катетом для заданого кута в прямокутному трикутнику називається співвідношенням дотичної. У вашому науковому або графічному калькуляторі запрограмовано дотичну, щоб ви могли визначити співвідношення\ dfrac {\ text {протилежна нога}} {\ text {суміжна нога}}\) для будь-якого кута в прямокутному трикутнику. Абревіатура від тангенса - tan.

Обчислення тангенсних функцій

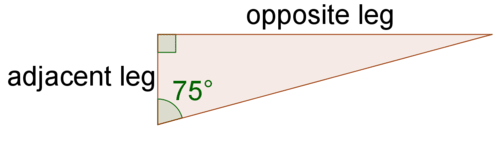
Використовуйте калькулятор, щоб знайти тангенс\(75^{\circ}\). Що являє собою ця величина?

Переконайтеся, що калькулятор знаходиться в режимі ступеня. Потім введіть «\(\tan(75)\)».

\(tan(75^{\circ})\approx 3.732\)

Це означає, що відношення довжини протилежної штанини до довжини сусідньої ноги для\(75^{\circ}\) кута в межах прямокутного трикутника складе приблизно 3,732.

Розв'язування невідомих значень

1. Вирішити для\(x\).

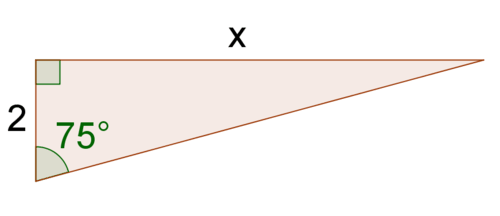
З попередньої проблеми ви знаєте, що співвідношення\(\dfrac{\text{opposite leg}}{\text{adjacent leg}} \approx 3.732\). Ви можете використовувати це для вирішення\(x\).

\ (\ begin {вирівняний}
\ dfrac {\ текст {протилежна нога}} {\ текст {сусідня нога}} &\ приблизно 3.732
\\ dfrac {x} {2} &\ приблизно 3.732\
x &\ приблизно 7.464
\ кінець {вирівняний}\)

2. Вирішити для\(x\) і\(y\).

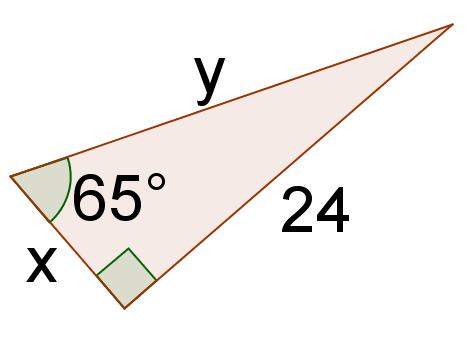
Ви можете використовувати\(65^{\circ}\) кут, щоб знайти правильне співвідношення між 24 і\(x\).

\ (\ почати {вирівняний}
\ тан\ лівий (65^ {\ circ}\ праворуч) &=\ dfrac {\ текст {протилежна нога}} {\ текст {сусідня нога}}\\
2.145 &\ приблизно\ dfrac {24} {x}\\
x &\ приблизно\ dfrac {24} {2.145}\
x &\ приблизно 11.189
\ кінець {вирівняний}\)

Зверніть увагу, що ця відповідь є лише приблизною, оскільки ви округлили значення\(\tan 65^{\circ}\). Точна відповідь буде включати в себе «загар». Точна відповідь:

\(x=\dfrac{24}{\tan 65^{\circ}}\)

Щоб вирішити для y, ви можете використовувати теорему Піфагора, оскільки це прямокутний трикутник.

\ (\ почати {масив} {r}
11.189^ {2} +24^ {2} =y^ {2}\\
701.194=y^ {2}\\
26.48=y
\ end {масив}\)

Приклад\(\PageIndex{1}\)

Раніше вас запитали, як змінюється дотичне відношення кута.

Рішення

Коли міра кута збільшується між\(0^{\circ}\) і\(90^{\circ}\), як змінюється дотичне відношення кута?

Зі збільшенням кута довжина його протилежної ніжки збільшується. Тому\(\dfrac{\text{opposite leg}}{\text{adjacent leg}}\) збільшується і, таким чином, збільшується величина дотичного відношення.

Приклад\(\PageIndex{2}\)

Тангенс говорить про співвідношення двох катетів прямокутного трикутника з заданим кутом. Чому дотичне відношення не працює однаково для неправильних трикутників?

Рішення

Два прямих трикутника з\(32^{\circ}\) кутом будуть схожі. Два непрямих трикутника з\(32^{\circ}\) кутом не обов'язково будуть схожі. Коефіцієнт дотичної працює для правильних трикутників, оскільки всі правильні трикутники із заданим кутом схожі. Коефіцієнт дотичної не працює однаково для неправильних трикутників, оскільки не всі неправильні трикутники із заданим кутом схожі. Ви можете використовувати співвідношення тангенсів лише для правильних трикутників.

Приклад\(\PageIndex{3}\)

Використовуйте калькулятор, щоб знайти тангенс\(45^{\circ}\). Що являє собою ця величина? Чому це значення має сенс?

Рішення

\(\tan(45^{\circ})=1\). Це означає, що відношення довжини протилежної ноги до довжини сусідньої ноги дорівнює 1 для прямих трикутників з\(45^{\circ}\) кутом.

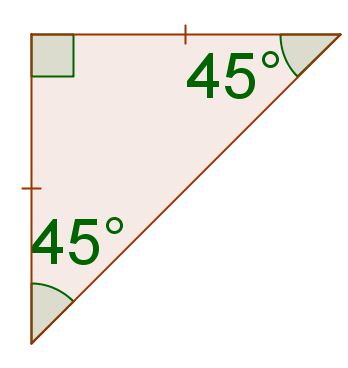
Це має мати сенс, оскільки прямі трикутники з\(45^{\circ}\) кутом рівнобедрені. Ніжки рівнобедреного трикутника конгруентні, тому співвідношення між ними буде дорівнює 1.

Приклад\(\PageIndex{4}\)

Вирішити для\(x\).

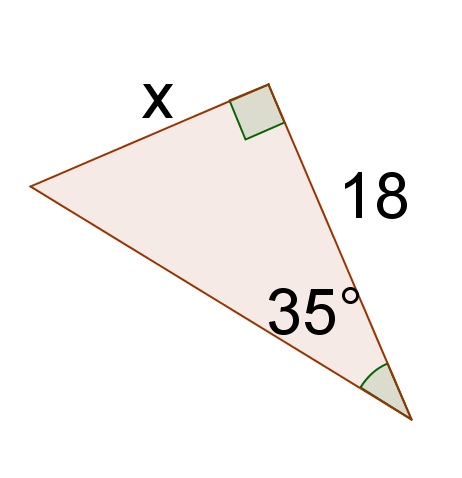
Рішення

Використовуйте дотичне відношення\(35^{\circ}\) кута.

\ (\ почати {вирівняний}
\ тан\ лівий (35^ {\ circ}\ праворуч) &=\ dfrac {\ текст {протилежна нога}} {\ текст {сусідня нога}}
\\ тан\ ліворуч (35^ {\ circ}\ праворуч) &=\ dfrac {x} {18}\
x &=18\ tan\ ліворуч (35^ {\ circ}\ праворуч)\\
х &\ приблизно 12.604
\ кінець { вирівняні}\)

Рецензія

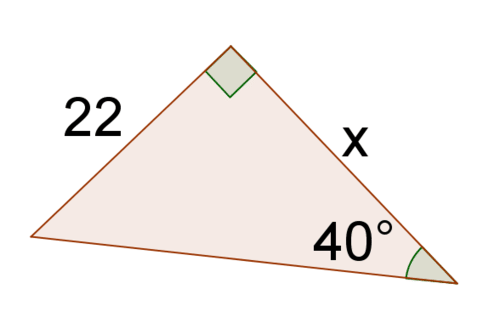
1. Чому все правильні трикутники з\(40^{\circ}\) кутом схожі? Яке це має відношення до тангенса?

2. Знайти тангенс\(40^{\circ}\).

3. Вирішити для\(x\).

4. Знайти тангенс\(80^{\circ}\).

5. Вирішити для\(x\).

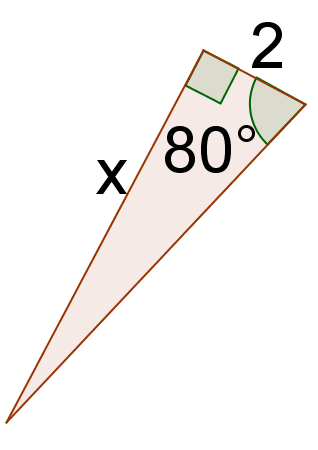
6. Знайти тангенс\(10^{\circ}\).

7. Вирішити для\(x\).

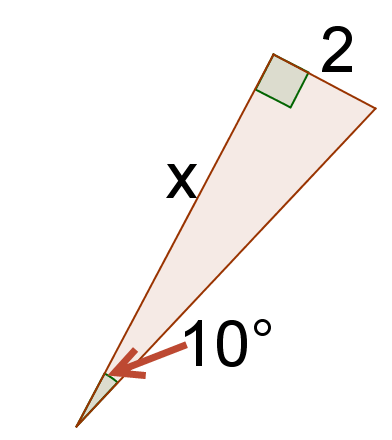
8. Ваша відповідь на #5 повинна бути такою ж, як і ваша відповідь на #7. Чому?

9. Знайти тангенс\(27^{\circ}\).

10. Вирішити для\(x\).

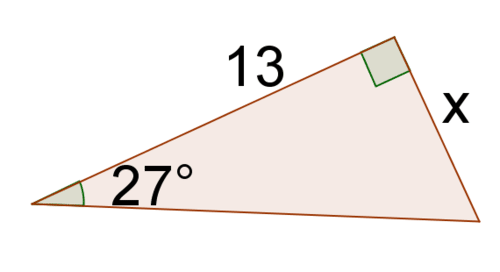
11. Знайти тангенс\(42^{\circ}\).

12. Вирішити для\(x\).

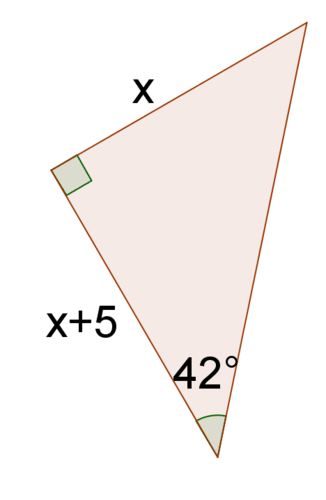
13. Прямокутний трикутник має\(42^{\circ}\) кут. Підстава трикутника, прилеглого до\(42^{\circ}\) кута, становить 5 дюймів. Знайдіть площу трикутника.

14. Нагадаємо, що співвідношення між сторонами трикутника 30-60-90 є\(1:\sqrt{3}:2\). Знайти тангенс\(30^{\circ}\). Поясніть, як це відповідає співвідношенням для трикутника 30-60-90.

15. Поясніть, чому має сенс, що значення дотичного відношення збільшується в міру того, як кут йде від\(0^{\circ}\) до\(90^{\circ}\).

Огляд (Відповіді)

Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 7.1.

Лексика

Термін	Визначення
Постулат подібності AA	Якщо два кути в одному трикутнику збігаються з двома кутами в іншому трикутнику, то два трикутника схожі.
Конгруентний	Конгруентні фігури ідентичні за розміром, формою і мірою.
Схожі	Дві фігури схожі, якщо вони мають однакову форму, але не обов'язково однакового розміру.
Тангенс	Тангенс кута в прямокутному трикутнику - це величина, знайдена діленням довжини сторони, протилежної заданому куту, на довжину сторони, прилеглої до даного кута.

Додаткові ресурси

Відео: Базова тригонометрія

Практика: ТАН