2.1.3: ГРІХ

Last updated

Oct 27, 2022
Save as PDF
- 2.1.2: Функції трига калькулятора
- 2.1.4: СОС

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Тригонометричні співвідношення на основі сторін прямокутних трикутників по відношенню до кута.

Розуміння синусів

Якову доводиться струнні вогні навколо карниза свого сараю з плоским дахом. Оскільки він боїться висоти, він хоче планувати це починання дуже ретельно. Він знає, що з міркувань безпеки сходи повинні робити кут $75^{\circ}$ або менше з землею. Якщо у Якова є сходи довжиною 6,5 метрів, щоб розмістити проти сторони сараю висотою 2,5 метра, то який кут буде робити сходи з землею? Джейкобу потрібно бути впевненим, що кут відповідає вимогам безпеки, перш ніж він поставить одну ногу на сходи. Як він може з'ясувати міру кута між сходами і землею?

У цьому понятті ви навчитеся розуміти тригонометричне співвідношення синуса.

Сінес

Тригонометрія - це галузь математики, яка використовується для визначення довжин сторін і вимірювання кутів з великою точністю. Ви будете розглядати тільки результати, отримані при використанні прямокутних трикутників.

Сторона прямокутного трикутника, розташована навпроти кута 90^ {\ circ}, є найдовшою стороною трикутника і називається гіпотенузою. Дві коротші сторони трикутника, які часто називають ніжками, мають специфічні назви стосовно розташування одного з гострих кутів прямокутного трикутника.

В обох трикутниках гіпотенуза протилежна прямому куту. У першому трикутнику кут, позначений червоним кольором, називається опорним кутом, і він використовується для назви ніжок трикутника. Міра опорного кута може бути задана або, можливо, доведеться розрахувати його міру. Як би там не було, один з гострих кутів буде посилатися в питанні або проблемі. Сторона поперек від опорного кута називається протилежною стороною. Третя сторона називається суміжною стороною, і саме сторона трикутника разом з гіпотенузою утворює опорний кут.

У другому трикутнику кут, позначений червоним кольором, називається опорним кутом, і він використовується для назви катетів цього трикутника. Сторона поперек від опорного кута називається протилежною стороною. Третя сторона називається суміжною стороною, і саме сторона трикутника разом з гіпотенузою утворює опорний кут.

Розташування гіпотенузи ніколи не змінюється, але розташування протилежної і сусідньої сторін залежить від того, який гострий кут є опорним кутом.

На кожній наведеній діаграмі позначте кожну сторону прямокутного трикутника як:

Гіпотенуза (H); Бічний протилежний опорний кут (O); Сторона, прилегла до опорного кута (A)

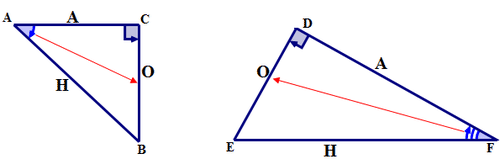
Співвідношення довжин сторін прямокутного трикутника називається тригонометричним відношенням. Ставлення довжини сторони, протилежної опорному куту, до довжини гіпотенузи відоме як відношення s ine. Коефіцієнт синуса пов'язаний з опорним кутом прямокутного трикутника, а не з прямим кутом.

Коефіцієнт синуса для першого трикутника можна записати словами так:

синус $\angle A=\dfrac{\text{side opposite} \angle A}{\text{hypotenuse}}$ або в скороченому вигляді як синус $\angle A=\dfrac{opposite}{hypotenuse}$

Коефіцієнт синуса для першого трикутника може бути записаний символами як:

$\sin A=\dfrac{BC}{AB}$

Коефіцієнт синуса для другого трикутника можна записати словами так:

синус $\angle F=\dfrac{\text{side opposite}\angle F}{\text{hypotenuse}}$ або в скороченому вигляді як синус $\angle F=\dfrac{opposite}{hypotenuse}$

Коефіцієнт синуса для першого трикутника може бути записаний символами як:

$\sin F=\dfrac{DE}{EF}$

Визначимо значення синусоїдного відношення кожного з гострих кутів, використовуючи наступний прямокутний трикутник. Висловіть співвідношення синусів словами і символами. Потім, використовуючи значення з відповідних сторін, замініть символи на цифри і висловити співвідношення спочатку у вигляді дробу, а потім у вигляді десяткового округлення до найближчої десятитисячної (чотири розряди після десяткової).

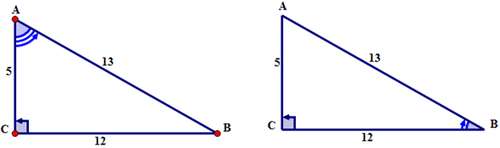
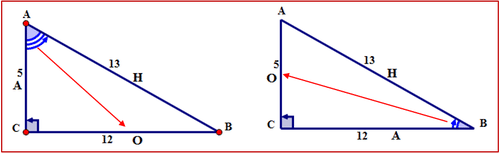
Для першого трикутника:

Спочатку щодо опорного кута А назвіть сторони трикутника.

Гіпотенуза знаходиться поперек від прямого кута. Протилежна сторона - поперек від $\angle A$ . Сторона поруч $\angle A$ є суміжною. Сторони позначені літерами Н, О, А відповідно.

Далі запишіть синусоїдальне співвідношення для $\angle A$ у всіх необхідних формах.

Слова:

синус $\angle A=\dfrac{opposite}{hypotenuse}$

Символи:

$\sin A=\dfrac{BC}{AB}$

Дріб:

$\sin A=\dfrac{12}{13}$

Десяткова:

$\sin A=0.9231$

Другий трикутник - це перший трикутник з\ кутом B як опорний кут. Зверніть увагу, що місця протилежної та сусідньої сторін змінилися від того місця, де вони були, коли\ кут А був опорним кутом.

Спочатку щодо опорного кута B назвіть сторони трикутника.

Гіпотенуза знаходиться поперек від прямого кута. Протилежна сторона - поперек від $\angle B$ . Сторона поруч $\angle B$ є суміжною. Сторони позначені літерами Н, О, А відповідно.

Далі запишіть синусоїдальне співвідношення для $\angle B$ у всіх необхідних формах.

Слова:

синус $\angle B=\dfrac{opposite}{hypotenuse}$

Символи:

$\sin B=\dfrac{AC}{AB}$

Дріб:

$\sin B=\dfrac{5}{13}$

Десяткова:

$\sin B=0.3846$

Якщо sInB=0.3846, то міру\ кута B можна знайти за допомогою калькулятора TI-84.

Пам'ятайте, ви вимірюєте кути в одиницях, званих градусами. Натискаємо режим і дивимося на екран.

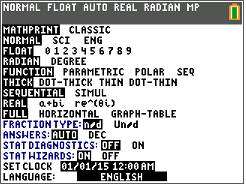
У четвертому ряду екрану DEGREE не виділяється.

Дотримуйтесь наведеної нижче історії натискань клавіш, щоб перевести калькулятор у режим DEGREE.

У четвертому рядку екрану тепер підсвічується DEGREE.

Далі дотримуйтесь історії натискань клавіш нижче, щоб знайти міру $\angle B$ .

Потім подивіться на екран калькулятора:

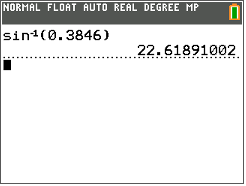
Округлите мірку кута до найближчої десятої.

$\angle B=22.6^{\circ}$

Відповідь: $22.6^{\circ}$

Приклад $\PageIndex{1}$

Раніше вам давали задачу про Якова і кут його сходів. Якову потрібно переконатися, що сходи роблять кут менше, ніж $75^{\circ}$ з землею? Джейкобу доведеться використовувати синусоїдальне співвідношення, щоб розібратися в цьому.

Рішення

Спочатку намалюйте та позначте прямокутний трикутник з наданою інформацією.

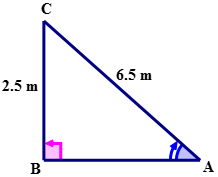
Далі назвіть сторони трикутника з посиланням на $\angle A$ .

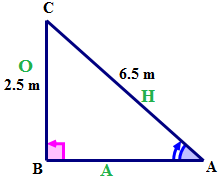
Далі висловлюйте співвідношення $\sin A$ за допомогою слів.

$\sin A=\dfrac{opposite}{hypotenuse}$

Далі виражаємо співвідношення за допомогою символів.

$\sin A=\dfrac{BC}{AC}$

Далі виражаємо співвідношення у вигляді дробу, використовуючи відповідні значення сторін.

$\sin A=\dfrac{2.5}{6.5}$

Далі виражаємо співвідношення у вигляді десяткового числа.

$\sin A=0.3846$

Далі скористайтеся функцією sin−1 на Ti-калькуляторі, щоб знайти міру\ кута A.

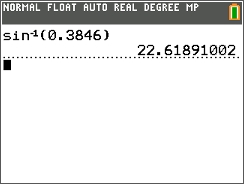
Потім запишіть міру $\angle A$ до найближчої десятої.

$\angle A=22.6^{\circ}$

Відповідь є $22.6^{\circ}$ .

Якову безпечно йти по сходах.

Приклад $\PageIndex{2}$

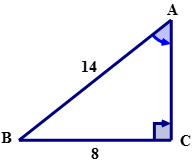
Використовуйте коефіцієнт синуса для обчислення міри $\angle A$ до найближчої десятої.

Рішення

По-перше, використовуючи $\angle A$ назву сторін трикутника.

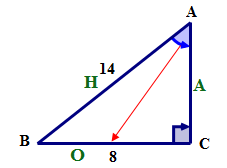
Далі прописуємо синусоїдальне співвідношення прописом.

$\sin A=\dfrac{opposite}{hypotenuse}$

Далі пишемо співвідношення, використовуючи символи.

$\sin A=\dfrac{BC}{AB}$

Далі виражаємо співвідношення у вигляді дробу, використовуючи значення відповідних сторін.

$\sin A=\dfrac{8}{14}$

Далі виражаємо співвідношення у вигляді десяткової коми з округленням до чотирьох знаків після десяткової.

$\sin A=0.5714$

Потім скористайтеся функцією зворотного синуса ( $\sin^{−1}$ ) на калькуляторі TI, щоб знайти міру $\angle A$ .

Потім подивіться на екран і округляйте міру кута до найближчої десятої.

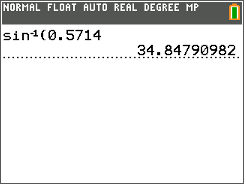
Зверніть увагу, не потрібно закривати дужку після того, як десяткова цифра була введена в калькулятор.

$\angle A=34.9^{\circ}$

Відповідь: $34.9^{\circ}$

Приклад $\PageIndex{3}$

Для наступного прямокутного трикутника висловіть SinB словами, символами, як дріб і десятковий.

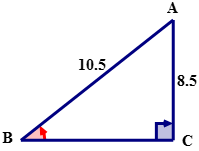
Рішення

Спочатку назвіть сторони трикутника, використовуючи опорний кут B.

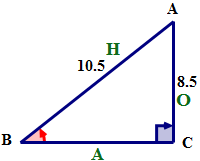
Далі висловлюємо співвідношення sInB за допомогою слів.

$\sin B=\dfrac{opposite}{hypotenuse}$

Далі виражаємо співвідношення за допомогою символів.

$\sin B=\dfrac{AC}{AB}$

Далі виражаємо співвідношення у вигляді дробу, використовуючи відповідні значення сторін.

$\sin B=\dfrac{8.5}{10.5}$

Потім висловіть відношення як десяткове число до десятитисячних.

$\sin B=0.8095$

Відповідь - 0.8095.

Приклад $\PageIndex{4}$

Якщо $\sin A=0.3872$ , яка міра $\angle A$ до найближчої десятої.

Рішення

Спочатку скористайтеся TI-калькулятором і слідкуйте за історією натискань клавіш.

Далі дивимося на екран калькулятора.

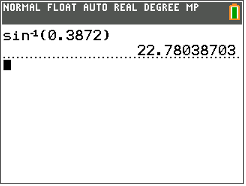
Потім запишіть міру $\angle A$ до найближчої десятої.

$\angle A=22.8^{\circ}$

Відповідь є $22.8^{\circ}$ .

Приклад $\PageIndex{5}$

Визначте міру\ кут B в наступному трикутнику.

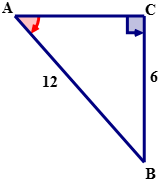
Рішення

Спочатку назвіть сторони трикутника.

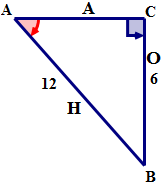
Далі висловлюємо співвідношення гріха А за допомогою слів.

$sin A=\dfrac{opposite }{hypotenuse}$

Далі виражаємо співвідношення за допомогою символів.

$\sin A=\dfrac{BC}{AB}$

Далі виражаємо співвідношення у вигляді дробу, використовуючи відповідні значення сторін.

$\sin A=\dfrac{6}{12}$

Далі виражаємо співвідношення у вигляді десяткового числа.

$\sin A=0.5$

Далі скористайтеся функцією sin−1 на TI-калькуляторі, щоб знайти міру $\angle A$ .

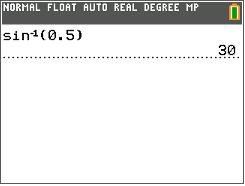
Потім напишіть міру $\angle A$ .

$\angle A=30^{\circ}$

Відповідь є $30^{\circ}$ .

Рецензія

Вирішіть кожну проблему.

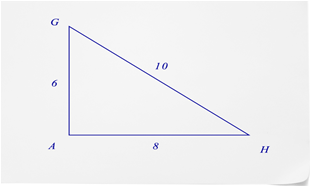
Що таке синус $\angle G$ ?
Що таке синус $\angle H$ ?
Чи можете ви знайти синус $\angle A$ ?

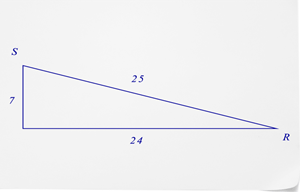
Що таке синус $\angle R$ ?
Що таке синус $\angle S$ ?

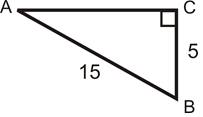
Що таке синус $\angle A$ ?
Що таке синус $\angle B$ ?
Яка довжина відсутньої сторони округлена до найближчої сотої?

Відповідь на кожне питання вірно або помилково.

Ви можете використовувати теорему Піфагора, щоб знайти довжину відсутньої сторони в прямокутному трикутнику.
Прямокутний трикутник повинен мати кут 90 градусів.
Коефіцієнт синуса - гіпотенуза над протилежною стороною.
Якщо ви знаєте тільки довжину боку, то можна з'ясувати всі бокові довжини.
Коефіцієнт синуса має відношення до довжини сторін.
Гіпотенуза завжди протилежна прямому куту.
Вам повинні бути вказані всі три довжини сторін, щоб з'ясувати співвідношення синуса.

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 7.13.

Лексика

Термін	Визначення
синус	Синус кута в прямокутному трикутнику - це величина, знайдена діленням довжини сторони, протилежної заданому куту, на довжину гіпотенузи.
Тригонометричні коефіцієнти	Співвідношення, які допомагають нам зрозуміти відносини між сторонами і кутами прямих трикутників.

Додаткові ресурси

Інтерактивний елемент

Відео: Вступ до тригонометричних функцій з використанням трикутників

Діяльність: Тригонометричні коефіцієнти з калькулятором Питання обговорення

Практика: Функції трига калькулятора

Реальний світ: Тангенс синусосинуса

Розуміння синусів

Сінес

Приклад2.1.3.1\PageIndex{1}

Приклад2.1.3.2\PageIndex{2}

Приклад2.1.3.3\PageIndex{3}

Приклад2.1.3.4\PageIndex{4}

Приклад2.1.3.5\PageIndex{5}

Рецензія

Огляд (Відповіді)

Лексика

Додаткові ресурси

Інтерактивний елемент

Приклад $\PageIndex{1}$

Приклад $\PageIndex{2}$

Приклад $\PageIndex{3}$

Приклад $\PageIndex{4}$

Приклад $\PageIndex{5}$