2.1.7: ВАРТІСТЬ CSC SEC
- Page ID
- 54653
Секансні, косекансні, котангенсні значення загальних кутів
Працюючи над фарбуванням сходів вашого діда, ви дивитеся на трикутну форму, зроблену стіною, яка підтримує сходи. Сходи виглядає так:

Ви думаєте про всі можливі відносини між сторонами. Ви вже знаєте, що існує три загальні відносини, звані синусом, косинусом і тангенсом.
Скільки інших ви можете знайти?
секанс, косеканс і котангенс Функції
Ми можемо визначити ще три функції також на основі прямокутного трикутника. Вони є зворотними синусом, косинусом і тангенсом.
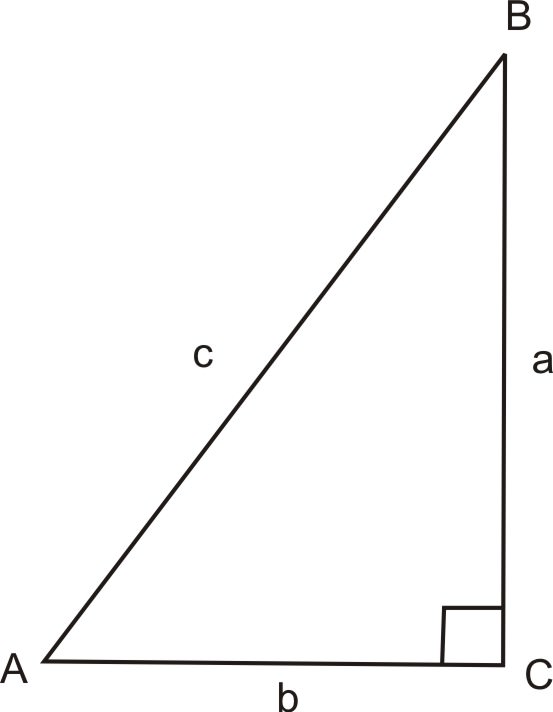
Якщо\(\sin A=\dfrac{a}{c}\), то визначення косеканса, або csc, є\(\csc A=\dfrac{c}{a}\).
Якщо\(\cos A=\dfrac{b}{c}\), то визначення секантного, або сек, є\(\sec A=\dfrac{c}{b}\).
Якщо\(\tan A=\dfrac{a}{b}\), то визначення котангенса, або ліжечка, є\(\cot A=\dfrac{b}{a}\).
Використовуйте визначення секанс, косеканс і котангенс для вирішення наступних завдань.
1. Знайдіть січну, косекансну та котангенс кута\(B\).
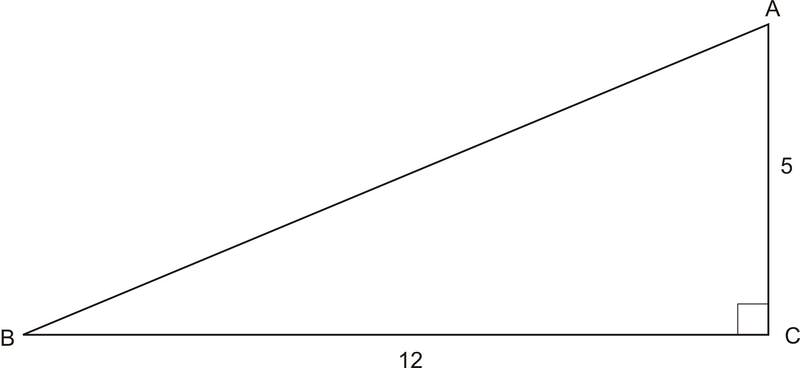
Спочатку треба знайти довжину гіпотенузи. Ми можемо зробити це за допомогою теореми Піфагора:
\ (\ почати {вирівняний}
5^ {2} +12^ {2} &=H ^ {2}\\
25+144 &=H^ {2}\\
169 &= H^ {2}\\
H &=13
\ кінець {вирівняний}\)
Тепер ми можемо знайти січний, косеканс і котангенс кута B:
\ (\ почати {масив} {l}
\ сек B =\ dfrac {\ текст {гіпотенуза}} {\ текст {сусідня сторона}} =\ dfrac {13} {12}
\ csc B=\ dfrac {\ текст {гіпотенуза}} {\ текст {протилежна сторона}} =\ dfrac {13} {5}\
\ cot B =\ dfrac {\ текст {сусідня сторона}} {\ текст {протилежна сторона}} =\ dfrac {12} {5}
\ end {масив}\)
2. Знайти січну, косекансну та котангенс кута A
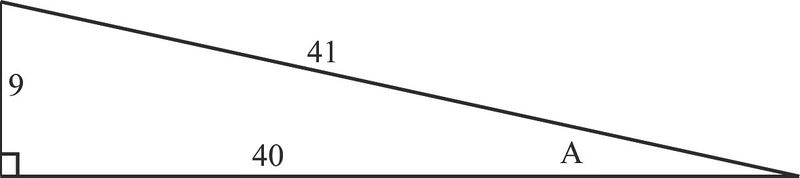
\ (\ почати {масив} {l}
\ сек A=\ dfrac {\ текст {гіпотенуза}} {\ текст {сусідня сторона}} =\ dfrac {41} {40}
\ csc A=\ dfrac {\ текст {гіпотенуза}} {\ текст {протилежна сторона}} =\ dfrac {41} {9}\
\ cot A=\ dfrac {\ текст {сусідня сторона}} {\ текст {протилежна сторона}} =\ dfrac {40} {9}
\ end {масив}\)
3. Знайдіть синус, косинус і тангенс кута\(A\), а потім використайте це для побудови сіканси, косеканси та котангенса кута
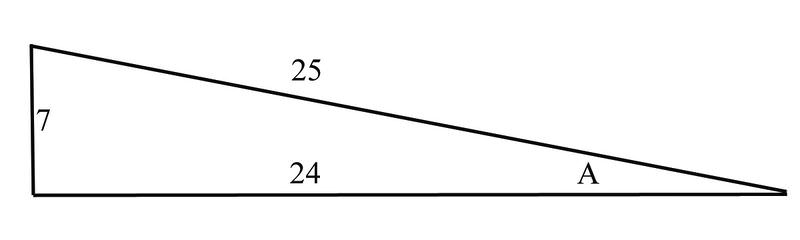
\ (\ почати {масив} {l}
\ sin A=\ dfrac {\ текст {протилежна сторона}} {\ текст {гіпотенуза}} =\ dfrac {7} {25}
\ cos A=\ dfrac {\ текст {гіпотенуза}} =\ dfrac {24} {25}\\ tan A=
\ dfrac {\ текст {протилежна сторона}} {\ текст {сусідня сторона}} =\ dfrac {7} {24}
\ end {масив}\)
Оскільки ми знаємо, що косеканс - це зворотний синус, секанс - зворотний синус, а котангенс - зворотний тангенс, ми можемо побудувати ці функції наступним чином:
\ (\ почати {масив} {л}
\ сек A=\ dfrac {1} {\ cos A} =\ dfrac {25} {24}\
\ csc A=\ dfrac {1} {\ sin A} =\ dfrac {25} {7}\
\ cot A=\ dfrac {1} {\ tan} =\ dfrac {24} 7}
\ end {масив}\)
Раніше вам давали проблему з приводу сходів вашого діда.
Дивлячись на трикутник за формою стіни, що підтримує сходи вашого діда:

Рішення
Ми бачимо, що існує кілька способів налагодити відносини між сторонами. В даному випадку нас цікавлять тільки співвідношення між сторонами, а значить одна сторона буде розділена іншою. Ми вже бачили деякі функції, такі як:
1) Сторона, протилежна куту, поділена на гіпотенузу (синусоїдальна функція)
2) Сторона, що прилягає до кута, поділена на гіпотенузу (функція косинуса)
3) Сторона, протилежна куту, розділена суміжною стороною (функція дотичної)
У цьому розділі ми ввели зворотні перераховані вище функції trig. Вони знаходять, приймаючи співвідношення між тими ж сторонами, показаними вище, за винятком зворотного чисельника та знаменника:
4) Гіпотенуза, розділена стороною, протилежною куту (функція косеканс)
5) Гіпотенуза, розділена стороною, прилеглою до кута (січна функція)
6) Сусідня сторона, розділена протилежною стороною (функція котангенса)
Використовуйте малюнок нижче, щоб допомогти вирішити наступні приклади.
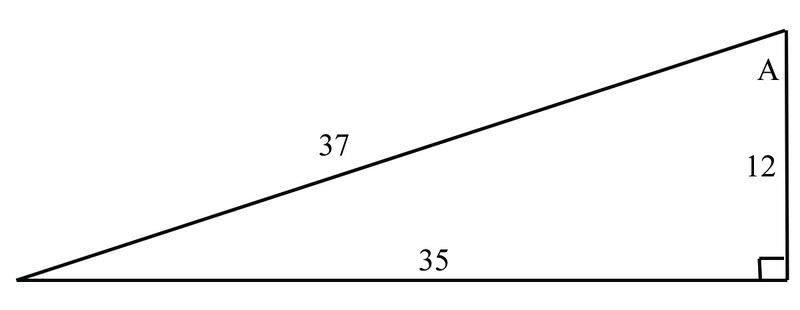
Знайдіть секанс\(\angle A\)
Рішення
Секансна функція визначена як be\(\dfrac{1}{\cos}\). З тих пір\(\cos=\dfrac{\text{adjacent}}{\text{hypotenuse}}\),\(\sec=\dfrac{\text{hypotenuse}}{\text{adjacent}}\).
\(\sec=\dfrac{\text{hypotenuse}}{\text{adjacent}}=\dfrac{37}{12}\approx 3.08\)
Знайдіть косеканс\(\angle A\)
Рішення
Функція косеканса визначена як be\(\dfrac{1}{\sin}\). З тих пір\(\sin=\dfrac{\text{opposite}}{\text{hypotenuse}}\),\(\csc=\dfrac{\text{hypotenuse}}{\text{opposite}}\).
\(\csc=\dfrac{\text{hypotenuse}}{\text{opposite}}=\dfrac{37}{35}\approx 1.06\)
Знайти котангенс\(\angle A\)
Рішення
Функція котангенса визначена як be\(\dfrac{1}{\tan}\). З тих пір\(\tan=\dfrac{\text{opposite}}{\text{adjacent}}\),\(\cot=\dfrac{\text{adjacent}}{\text{opposite}}\).
\(\cot=\dfrac{\text{adjacent}}{\text{opposite}}=\dfrac{12}{35} \approx .34\)
Рецензія
Використовуйте діаграму нижче для питань 1-3.
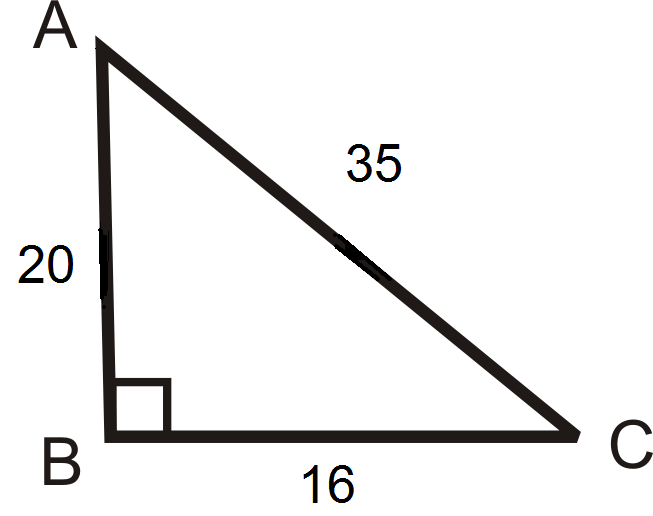
- Знайти\(\csc A\) і\(\csc C \).
- Знайти\(\sec A\) і\(\sec C\).
- Знайти\(\cot A\) і\(\cot C\).
Скористайтеся схемою, щоб заповнити пробіли нижче.
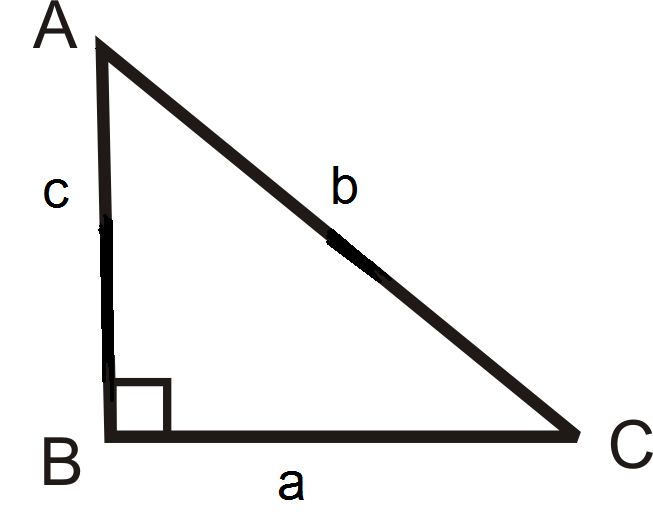
- \(\cot A=\dfrac{?}{?}\)
- \(\csc C =\dfrac{?}{?}\)
- \(\cot C=\dfrac{?}{?}\)
- \(\sec C=\dfrac{?}{?}\)
- \(\csc A=\dfrac{?}{?}\)
- \(\sec A=\dfrac{?}{?}\)
З питань 4-9 можна зробити висновок наступне. Заповніть заготовки.
- \(\sec \text{_____}=\csc A\)і\(\csc \text{_____}=\sec A\).
- \(\cot A\)і\(\cot C\) є _________ один одного.
- Поясніть, чому csc кута завжди буде більше 1.
- Використовуйте свої знання про трикутники 45-45-90, щоб знайти косеканс, секанс та котангенс кута 45 градусів.
- Використовуйте свої знання 30-60-90 трикутників, щоб знайти косеканс, січний і котангенс кута 30 градусів.
- Використовуйте свої знання 30-60-90 трикутників, щоб знайти косеканс, січний і котангенс кута 60 градусів.
- Зі збільшенням ступеня кута буде збільшуватися або зменшуватися котангенс кута? Поясніть.
Огляд (Відповіді)
Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 1.9.
Лексика
| Термін | Визначення |
|---|---|
| косеканс | Косеканс кута в прямокутному трикутнику - це залежність, знайдена діленням довжини гіпотенузи на довжину сторони, протилежної заданому куту. Це зворотна функція синуса. |
| котангенс | Котангенс кута в прямокутному трикутнику - це залежність, знайдена шляхом ділення довжини сторони, прилеглої до даного кута, на довжину сторони, протилежної заданому куту. Це зворотна функція дотичної. |
| січний | Секанс кута в прямокутному трикутнику - це величина, знайдена діленням довжини гіпотенузи на довжину сторони, прилеглої до заданого кута. Співвідношення секансів - це зворотне співвідношення косинусів. |