2.1.4: СОС
- Page ID
- 54635
Визначте косинус заданих довжин сторін
Розуміння косинусів

Роджер розмістив сходи довжиною 12 футів проти сторони будинку таким чином, що підніжжя сходів знаходиться в 5 футах від основи будинку. Коли Роджер готується піднятися по сходах, щоб очистити дощові жолоби будинку, його сусід кричить йому: «Вам краще відрегулювати цю сходи. Кут між сходами і землею повинен бути менше»\(75^{\circ}\).
Роджер відступив і подивився на положення сходів. «Він міг би мати рацію», - подумав Роджер. «Я повинен з'ясувати розмір цього кута, перш ніж піднятися на цю сходи».
Як же Роджер може обчислити міру кута?
У цьому понятті ви навчитеся розуміти тригонометричне співвідношення косинуса.
косинус
Тригонометрія - це галузь математики, яка використовується для визначення довжин сторін і вимірювання кутів з великою точністю. Співвідношення довжин сторін прямокутного трикутника називається тригонометричним відношенням. Ставлення довжини сторони поряд з опорним кутом до довжини гіпотенузи відоме як відношення косинусів. Гострий кут прямокутного трикутника утворюється гіпотенузою і одним з катетів трикутника. Цю ніжку називають суміжною стороною опорного кута. Співвідношення косинусів - це відношення сусідньої сторони до гіпотенузи.
На кожній наведеній діаграмі позначте кожну сторону прямокутного трикутника як:
Гіпотенуза (H); Бічний протилежний опорний кут (O); Сторона, прилегла до опорного кута (A).
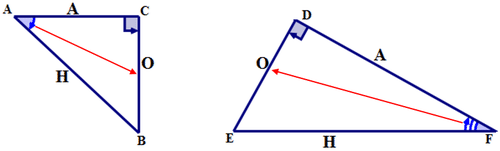
Коефіцієнт косинусів для першого трикутника можна записати такими словами:
косинус\(\angle A=\dfrac{\text{side adjacent }\angle A}{\text{hypotenuse}}\) або в скороченому вигляді як косинус\(\angle A=\dfrac{\text{adjacent}}{\text{hypotenuse}}\)
Коефіцієнт косинусів для першого трикутника може бути записаний символами як:
\(\cos A=\dfrac{AC}{AB}\)
Коефіцієнт косинусів для другого трикутника можна записати словами так:
косинус\(\angle F = \dfrac{\text{side adjacent }\angle F}{\text{hypotenuse}}\) або в скороченому вигляді як косинус\(\angle F=\dfrac{\text{adjacent}}{\text{hypotenuse}}\)
Коефіцієнт косинусів для другого трикутника можна записати символами як:
\(\cos F=\dfrac{DF}{EF}\)
Визначимо значення співвідношення косинусів кожного з гострих кутів за допомогою наступного прямокутного трикутника. Висловіть співвідношення косинусів словами і символами. Потім, використовуючи значення з відповідних сторін, замініть символи на цифри і висловити співвідношення спочатку у вигляді дробу, а потім у вигляді десяткового округлення до найближчої десятитисячної (чотири розряди після десяткової).
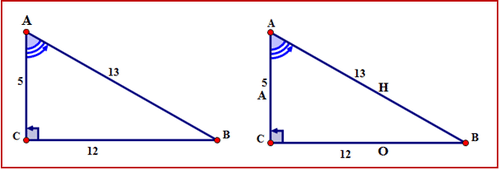
\(\Delta ABC\)з\(\angle A\) як опорний кут.
Спочатку назвіть сторони трикутника.
Гіпотенуза знаходиться поперек від прямого кута. Протилежна сторона поперек від\ кута А. Сторона поруч\ кут A є суміжною. Сторони позначені літерами Н, О, А відповідно.
Далі запишіть співвідношення\(\angle A\) косинусів для у всіх необхідних формах.
Слова:
косинус\(\angle A=\dfrac{\text{adjacent}}{\text{hypotenuse}}\)
Символи:
\(\cos A=\dfrac{AC}{AB}\)
Дріб:
\(\cos A=\dfrac{5}{13}\)
Десяткова:
\(\cos A=0.3846\)
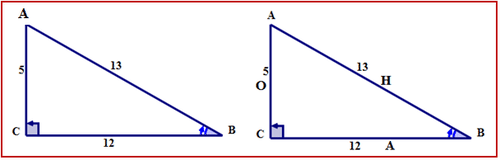
\(\Delta ABC\)з\(\angle B\) як опорний кут.
Зверніть увагу, що місця протилежної та сусідньої сторін змінилися з того місця, де вони були, коли\(\angle A\) був опорний кут.
Спочатку назвіть сторони трикутника.
Гіпотенуза знаходиться поперек від прямого кута. Протилежна сторона - поперек від\(\angle B\). Сторона поруч\(\angle B\) є суміжною. Сторони позначені літерами Н, О, А відповідно.
Далі запишіть співвідношення\(\angle B\) косинусів для у всіх необхідних формах.
Слова:
косинус\(\angle B=\dfrac{\text{adjacent}}{\text{hypotenuse}}\)
Символи:
\(\cos B=\dfrac{BC}{AB}\)
Дріб:
\(\cos B=\dfrac{12}{13}\)
Десяткова:
\(\cos B=0.9231\)
Якщо\(\cos A=0.3846\), то міру\(\angle A\) можна знайти за допомогою функції зворотного косинуса на TI- калькуляторі.
По-перше, дотримуйтесь історії натискань клавіш нижче, щоб обчислити міру\(\angle A\).
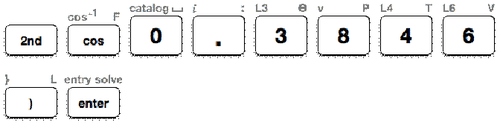
Далі подивіться на екран калькулятора, щоб побачити міру\(\angle A\).
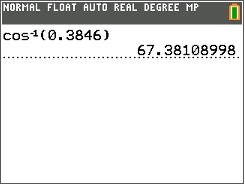
Потім запишіть міру\(\angle A\) до найближчої десятої.
\(\angle A=67.4^{\circ}\)
Відповідь:\(67.4^{\circ}\)
Раніше вам давали проблему з приводу Роджера і драбини. Йому потрібно з'ясувати кут, який сходи робить з землею.
Як же Роджер може з'ясувати міру кута?
Рішення
Він може використовувати співвідношення косинусів.
Спочатку намалюйте та позначте прямокутний трикутник, щоб змоделювати проблему.
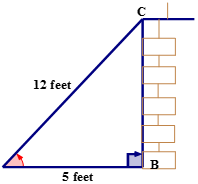
Далі назвіть сторони трикутника.
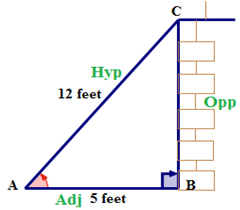
Далі пишемо співвідношення косинусів прописом.
\(\cos A=\dfrac{\text{adjacent}}{\text{hypotenuse}}\)
Далі пишемо співвідношення, використовуючи символи.
\(\cos A=\dfrac{AB}{AC}\)
Далі виражаємо співвідношення у вигляді дробу, використовуючи значення відповідних сторін.
\(\cos A=\dfrac{5}{12}\)
Далі виражаємо співвідношення у вигляді десяткової коми з округленням до чотирьох знаків після десяткової.
\(\cos A=0.4167\)
Далі скористайтеся оберненою функцією косинуса (cos−1) на калькуляторі TI, щоб знайти міру\(\angle A\).
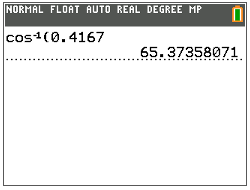
Потім запишіть міру\(\angle A\) до найближчої десятої.
\(\angle A=65.4^{\circ}\)
Відповідь:\(65.4^{\circ}\)
Міра\(\angle A\) є\(65.4^{\circ}\). Це менше, ніж\(75^{\circ}\) так Роджер може відремонтувати дощові жолоби.
Скористайтеся співвідношенням косинусів для обчислення міри\(\angle A\) до найближчої десятої.
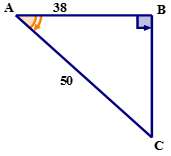
Рішення
По-перше, за допомогою опорного кута назвіть сторони трикутника.
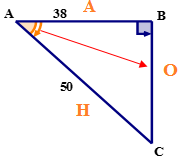
Далі пишемо співвідношення косинусів прописом.
\(\cos A=\dfrac{\text{adjacent}}{\text{hypotenuse}}\)
Далі пишемо співвідношення, використовуючи символи.
\(\cos A=\dfrac{AB}{AC}\)
Далі виражаємо співвідношення у вигляді дробу, використовуючи значення відповідних сторін.
\(\cos A=\dfrac{38}{50}\)
Далі виражаємо співвідношення у вигляді десяткової коми з округленням до чотирьох знаків після десяткової.
\(\cos A=0.76\)
Десяткова кома закінчується. Ви можете записати десяткове число як 0.7600, але це не обов'язково.
Далі скористайтеся оберненою функцією косинуса (\(\cos^{−1}\)) на калькуляторі TI, щоб знайти міру\(\angle A\).
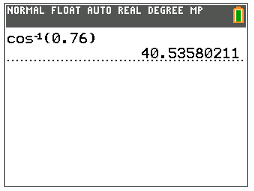
Потім запишіть значення\(\angle A\) до найближчої десятої.
\(\angle A=40.5^{\circ}\)
Відповідь:\(40.5^{\circ}\)
Якщо\(\cos B=0.7984\), яка міра\(\angle B\) до найближчої десятої.
Рішення
Спочатку скористайтеся Ti-калькулятором для визначення міри за\(\angle B\) допомогою функції зворотного косинуса (\ (\ cos^ {−1}) на калькуляторі. Ця функція знаходиться над кнопкою cos на калькуляторі. Щоб отримати доступ до цієї функції, натисніть
Далі введіть десяткове значення 0.7984 в дужках, де миготить курсор.
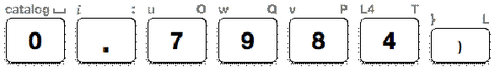
Далі натискаємо enter і на екрані калькулятора відобразиться міра кута.

Потім запишіть міру\(\angle B\) до найближчої десятої.
\(\angle B=32.0^{\circ}\).
Відповідь:\(32.0^{\circ}\)
Для наступного рішення, яке показує використання коефіцієнта косинусів для обчислення міри\ кута B, намалюйте та позначте прямокутний трикутник ABC, який використовувався для вирішення.
\ (\ почати {вирівняний}
\ cos B &=\ frac {\ текст {суміжний}} {\
текст {гіпотенуза}}\\ cos B &=\ FRAC {B}\
\ cos B &=\ frac {36} {76.7}
\ cos B &= 0.4694\
\ cos ^ {-1} (\ cos B) &=\ cos {-1} (0.4694)\\
\ кут B &=62.00454372\\
\ кут B &= 62.0^ {\ circ}
\ кінець {вирівняний}\)
Рішення
Спочатку запишіть те, що ви знаєте з рішення.
\(\Delta ABC\)являє собою прямокутний трикутник.
\(\overline{BC}\)є суміжною стороною трикутника.
\(\overline{BC}\)має довжину 36.
\(\overline{AB}\)- гіпотенуза трикутника.
\(\overline{AB}\)має довжину 76,7.
\(\angle B\)є опорним кутом.
Далі використовуйте записану інформацію, щоб намалювати та позначити трикутник.
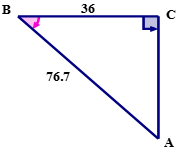
Вищевказаний трикутник представляє проблему.
Для заданого прямокутного трикутника використовуйте коефіцієнт косинусів для обчислення міри\(\angle A\) до найближчої десятої.
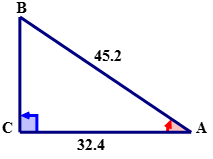
Рішення
По-перше, за допомогою опорного кута назвіть сторони трикутника.
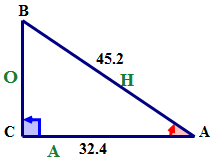
Далі пишемо співвідношення косинусів прописом.
\(\cos A=\dfrac{\text{adjacent}}{\text{hypotenuse}}\)
Далі пишемо співвідношення, використовуючи символи.
\(\cos A=\dfrac{AC}{AB}\)
Далі виражаємо співвідношення у вигляді дробу, використовуючи значення відповідних сторін.
\(\cos A=\dfrac{32.4}{45.2}\)
Далі виражаємо співвідношення у вигляді десяткової коми з округленням до чотирьох знаків після десяткової.
\(\cos A=0.7168\)
Далі скористайтеся оберненою функцією косинуса (\(\cos^{−1}\)) на калькуляторі TI, щоб знайти міру\(\angle A\).

Потім запишіть міру\(\angle A\) до найближчої десятої.
\(\angle A=44.2^{\circ}\).
Відповідь:\(44.2^{\circ}\)
Рецензія
Вирішіть кожну проблему.
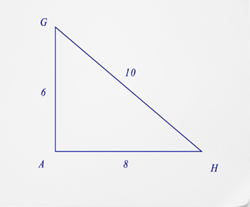
- Що таке косинус\(\angle G\)?
- Що таке косинус\(\angle H\)?
- Як визначити косинус?
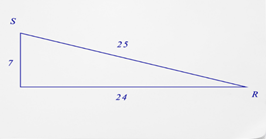
4. Що таке косинус\(\angle R\)?
5. Що таке косинус\(\angle S\)?
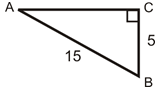
- Що таке косинус\(\angle A\)?
- Що таке косинус\(\angle B\)?
- Яка довжина відсутньої сторони округлена до найближчої сотої?
Дайте відповідь на кожне з наступних питань.
- Чи пов'язаний косинус з кутом?
- Вам потрібно знати довжини сторін трикутника, щоб написати косинус?
- Яка довжина сторін вам потрібна?
- \(\dfrac{5}{20}\)Якби косинус був би числовим значенням косинуса?
- \(\dfrac{5}{25}\)Якби косинус був би числовим значенням косинуса?
- \(\dfrac{3}{33}\)Якби косинус був би числовим значенням косинуса?
- \(\dfrac{12}{14}\)Якби косинус був би числовим значенням косинуса?
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 7.14.
Лексика
| Термін | Визначення |
|---|---|
| косинус | Косинус кута в прямокутному трикутнику - це величина, знайдена діленням довжини сторони, прилеглої до даного кута, на довжину гіпотенузи. |
| Тригонометричні коефіцієнти | Співвідношення, які допомагають нам зрозуміти відносини між сторонами і кутами прямих трикутників. |