2.1.1: Тригонометрія прямокутного трикутника

Синус, косинус, тангенс та інші співвідношення сторін прямокутного трикутника.

Синус, косинус і тангенс

Тригонометрія - це вивчення взаємозв'язків між сторонами і кутами прямих трикутників. Ніжки називаються суміжними або протилежними в залежності від того, який гострий кут використовується.

Малюнок$\PageIndex{1}$

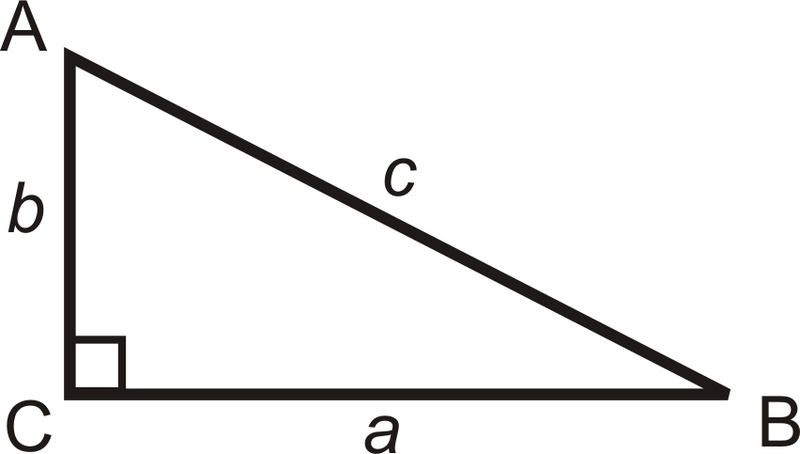
$\begin{aligned} a \text{ is adjacent to } \angle B \qquad a \text{ is opposite } \angle A \\ b \text{ is adjacent to } \angle A \qquad b \text{ is opposite } \angle B\\ c \text{ is the hypotenuse }\end{aligned}$

Три основні тригонометричні співвідношення називаються синусом, косинусом і тангенсом. Для прямокутного трикутника △ ABC ми маємо:

\ (\ почати {вирівняний}
\ текст {синус Співвідношення:}\ dfrac {\ text {протилежний катет}} {\ text {гіпотенуза}}\ qquad\ sin A=\ dfrac {a} {c} {c} {косинус Коефіцієнт:}
\ dfrac {\ текст {\ текст {\ текст {сусідня нога} {текст {гіпотенуза}}\ qquad\ cos A=\ dfrac {b} {c}\ текст {або}\ cos B=\ dfrac {a} {c}\ \
\ text {Дотичне співвідношення:}\ dfrac {\ текст {протилежна нога}} {\ текст {сусідня ніжка}}\ qquad\ tan A=\ dfrac {a} {b}\ text {або}\ tan B =\ dfrac {b} {a}
\ кінець {вирівняний}\)

Простий спосіб запам'ятати співвідношення - використовувати SOH-CAH-TOA.

Малюнок$\PageIndex{2}$

Кілька важливих моментів:

• Завжди зменшуйте коефіцієнти (дроби), коли можете.
• Використовуйте теорему Піфагора, щоб знайти відсутню сторону (якщо така є).
• Якщо в знаменнику присутній радикал, раціоналізуйте знаменник.

Що робити, якщо вам дали прямокутний трикутник і сказали, що його сторони вимірюють 3, 4 і 5 дюймів? Як ви могли знайти синус, косинус і тангенс одного з непрямих кутів трикутника?

Приклад$\PageIndex{1}$

Знайти синус, косинус і тангенс співвідношення$\angle A$.

Малюнок$\PageIndex{3}$

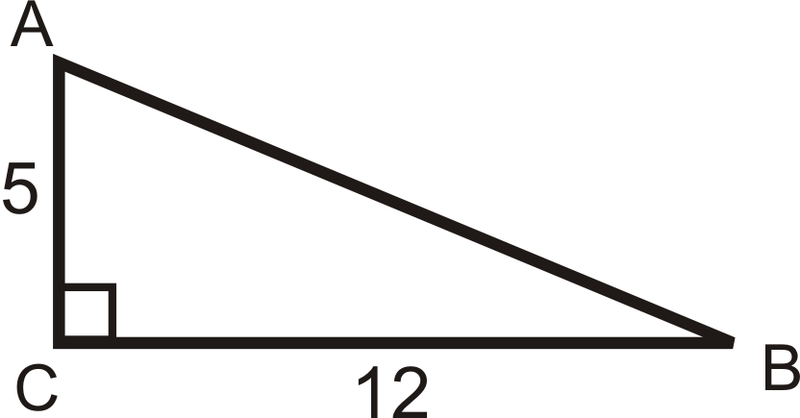
Рішення

Для початку нам потрібно скористатися теоремою Піфагора, щоб знайти довжину гіпотенузи.

\ (\ почати {вирівняний}
5^ {2} +12^ {2} &=c^ {2}\\
13 &=c\ кінець {вирівняний}\)

\ (\ почати {вирівняний}
\ sin A &=\ dfrac {l e g\ текст {протилежний}\ кут A} {\ текст {гіпотенуза}} =\ dfrac {12} {13} &\ cos A=\ dfrac {\ текст {\ text {кут A} {\ text {гіпотенуза}} =\ dfrac {5} {13},\\ tan A &=
\ dfrac {\ text {нога навпроти}\ кут A} {\ text {нога прилягає до}\ кут A} =\ dfrac {12} {5}
\ кінець {вирівняний}\)

Приклад$\PageIndex{2}$

Знайти синус, косинус і тангенс$\angle B$.

Малюнок$\PageIndex{4}$

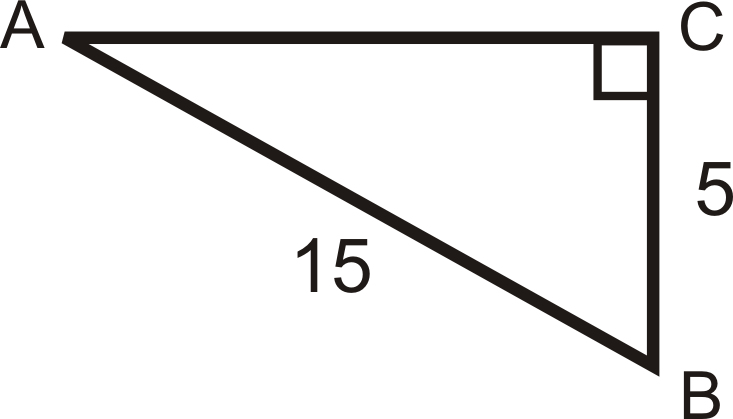
Знайдіть довжину відсутньої сторони.

Рішення

\ (\ почати {
вирівняний} A C ^ {2} +5^ {2} &=15^ {2}\
A C^ {2} &=200\
A C &=10\ sqrt {2}\ кінець {вирівняний}\)

\ (\ почати {вирівняний}\ sin B &=\ dfrac {10\ sqrt {2}} {15} =\ dfrac {2}} {3}\ квад\ cos B=\ dfrac {5} {15} =\ dfrac {1} {3}\ квад\ тан B =\ dfrac {10\ sqrt {2}} {5} =2\ sqrt {2}
\ кінець {вирівняний}\)

Приклад$\PageIndex{3}$

Знайти синус, косинус і тангенс$30^{\circ}$.

Малюнок$\PageIndex{5}$

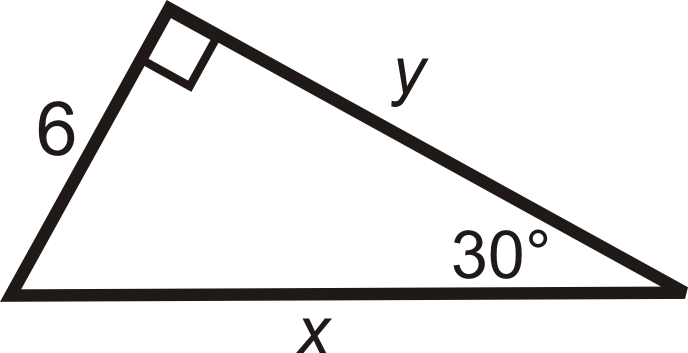
Рішення

Це трикутник 30-60-90. Коротка нога - 6,$y=6\sqrt{3}$ і$x=12$.

$\sin 30^{\circ}=\dfrac{6}{12}=\dfrac{1}{2} \qquad \cos30^{\circ}=\dfrac{6\sqrt{3}}{12}=\dfrac{\sqrt{3}}{2} \qquad \tan 30^{\circ}=\dfrac{6}{6\sqrt{3}}=\dfrac{1}{\sqrt{3}}\cdot \dfrac{\sqrt{3}}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}$

Приклад$\PageIndex{4}$

Дайте відповідь на питання щодо наступного зображення. Зменшити всі фракції.

Малюнок$\PageIndex{6}$

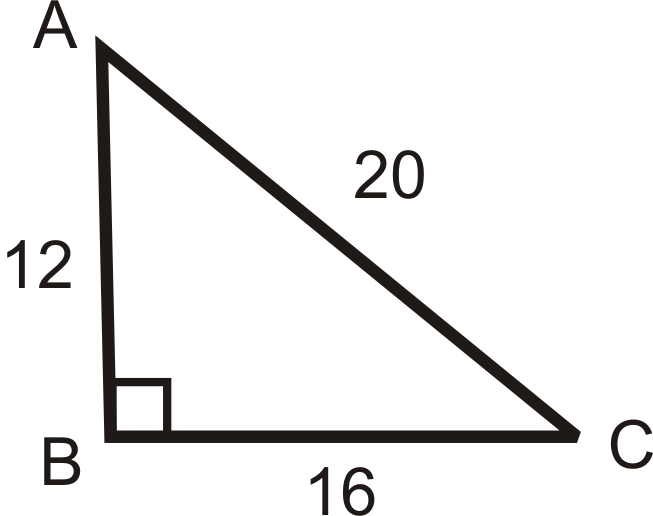
Що таке$\sin A$$\cos A$, і$\tan A$?

Рішення

\ (\ почати {масив} {л}
\ sin A=\ dfrac {16} {20} =\ dfrac {4} {5}\
\ cos A=\ dfrac {12} {20} =\ dfrac {3} {5}\
\ tan A=\ dfrac {16} {12} =\ dfrac {4} {3}
\ кінець {масив}\)

Рецензія

Скористайтеся схемою, щоб заповнити пробіли нижче.

Малюнок$\PageIndex{7}$

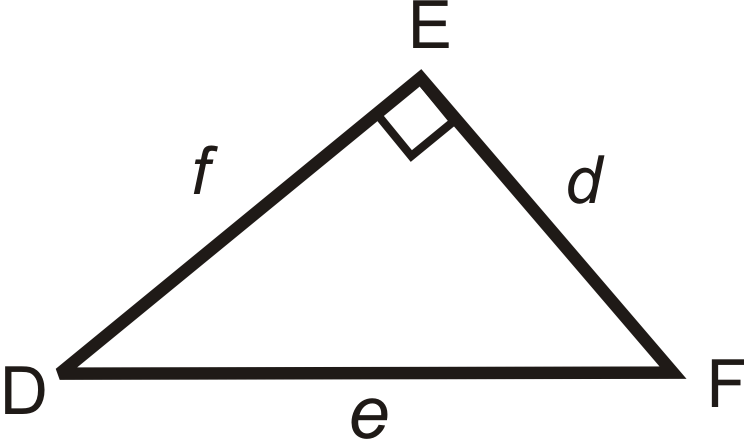
1. $\tan D=\dfrac{?}{?}$
2. $\sin F=\dfrac{?}{?}$
3. $\tan F=\dfrac{?}{?}$
4. $\cos F=\dfrac{?}{?}$
5. $\sin D=\dfrac{?}{?}$
6. $\cos D=\dfrac{?}{?}$

З питань 1-6 можна зробити висновок наступне. Заповніть заготовки.

7. $\cos \underline{\qquad}=\sin F$і$\sin \underline{\qquad}=\cos F$.
8. $\tan D$і$\tan F$ є _________ один одного.

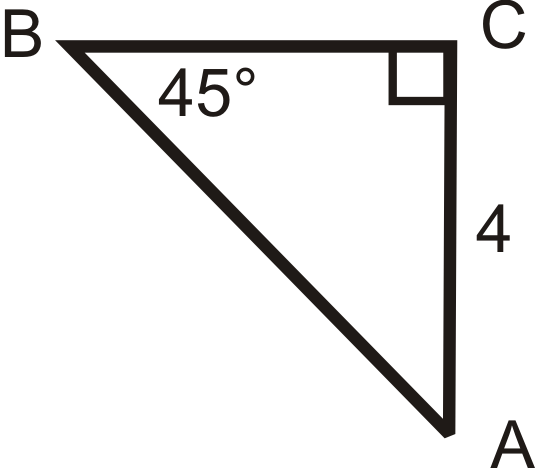
Знайти синус, косинус і тангенс$\angle A$. Зменшити всі фракції і радикали.

9. 
   

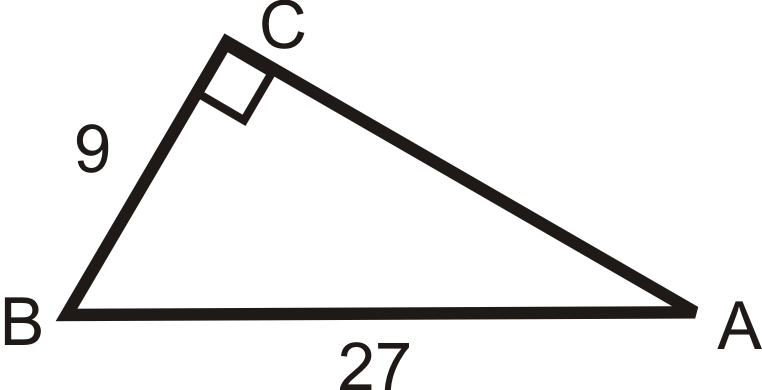
   Малюнок$\PageIndex{8}$

10. 

    Малюнок$\PageIndex{9}$

11. 

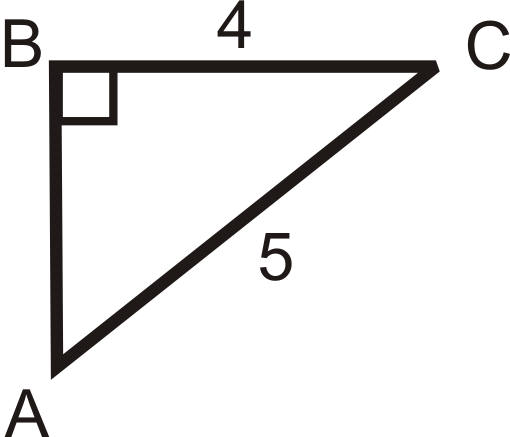
    Малюнок$\PageIndex{10}$

12. 

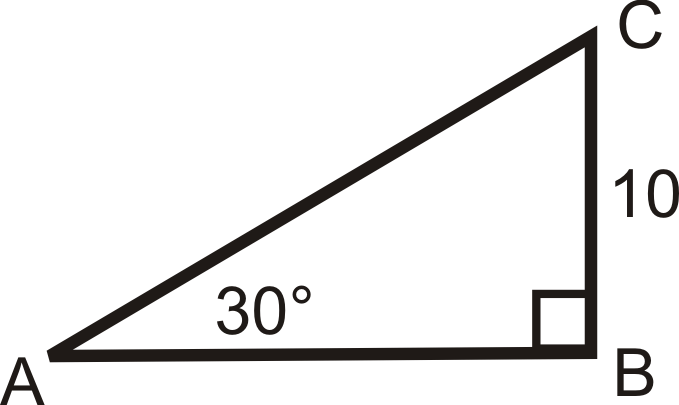
    Малюнок$\PageIndex{11}$

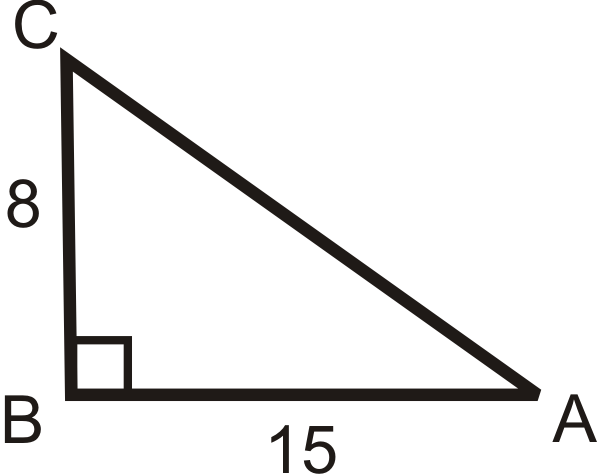13. Малюнок\(\PageIndex{12}\)

Огляд (Відповіді)

Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 8.7.

Ресурси

Лексика

Термін	Визначення
Гострий кут	Гострий кут - це кут з мірою менше 90 градусів.
Сусідні кути	Два кути є суміжними, якщо вони поділяють сторону і вершину. Слово «суміжний» означає «поруч» або «поруч з».
Гіпотенуза	Гіпотенуза прямокутного трикутника - найдовша сторона прямокутного трикутника. Вона знаходиться поперек від прямого кута.
Ніжки прямокутного трикутника	Ніжки прямокутного трикутника - це дві коротші сторони прямокутного трикутника. Ноги примикають до прямого кута.
протилежний	Протилежність числа$x$ є$−x$. Число і його протилежність завжди дорівнюють нулю.
Теорема Піфагора	Теорема Піфагора - це математична залежність між сторонами прямокутного трикутника, задана$a^2+b^2=c^2$, де a і b - катети трикутника, а c - гіпотенуза трикутника.
Радикальний	Знак$\sqrt$, або квадратний корінь.
синус	Синус кута в прямокутному трикутнику - це величина, знайдена діленням довжини сторони, протилежної заданому куту, на довжину гіпотенузи.
Тригонометричні коефіцієнти	Співвідношення, які допомагають нам під\ tan d відносини між сторонами і кутами прямих трикутників.

Додаткові ресурси

Інтерактивний елемент

Відео: Вступ до тригонометричних функцій U\ sin g Трикутники

Діяльність: Синус, косинус, Тангенс обговорення Питання

Навчальні посібники: Посібник з вивчення тригонометричних коефіцієнтів

Практика: Тригонометрія прямокутного трикутника

Реальний світ: Тангенс косинуса синуса