1.10:45-45-90 Прямі трикутники

Час катета$\sqrt{2}$ дорівнює гіпотенузі.

45-45-90 Прямі трикутники

Прямокутний трикутник з конгруентними ніжками та гострими кутами - це рівнобедрений прямокутний трикутник. Цей трикутник ще називають трикутником 45-45-90 (названий на честь кутових мір).

Малюнок$\PageIndex{1}$

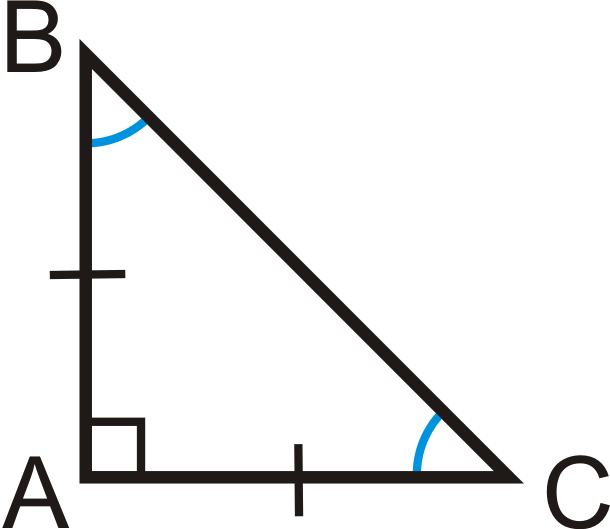
$\Delta ABC$є прямокутним трикутником з$m\angle A=90^{\circ}$,$\overline{AB} \cong \overline{AC}$ і$m\angle B=m\angle C=45^{\circ}$.

45-45-90 Теорема: Якщо прямокутний трикутник рівнобедрений, то його сторони знаходяться в співвідношенні$x:x:x\sqrt{2}$. Для будь-якого рівнобедреного прямокутного трикутника катети є$x$ і гіпотенуза завжди$x\sqrt{2}$.

Що робити, якщо вам дали рівнобедрений прямокутний трикутник і довжину однієї з його сторін? Як ви могли з'ясувати довжини його інших сторін?

Приклад$\PageIndex{1}$

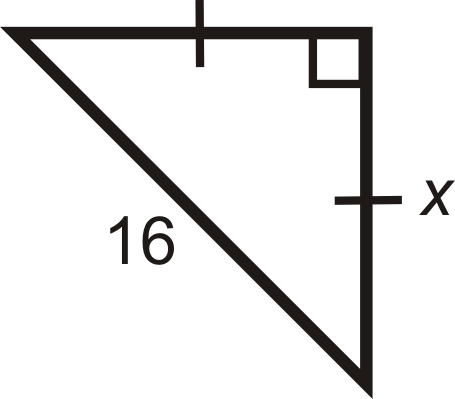
Знайти довжину$x$.

Рішення

Використовуйте$x:x:x\sqrt{2}$ співвідношення.

Тут нам дається гіпотенуза. Вирішити для$x$ в співвідношенні.

$\begin{aligned} x\sqrt{2} =16\\ x=16\sqrt{2}\cdot \dfrac{\sqrt{2}}{\sqrt{2}}=\dfrac{16\sqrt{2}}{2}=8\sqrt{2} \end{aligned}$

Приклад$\PageIndex{2}$

Знайти довжину$x$, де$x$ - гіпотенуза трикутника 45-45-90 з довжинами катетів$5\sqrt{3}$.

Рішення

Використовуйте$x:x:x\sqrt{2}$ співвідношення.

$x=5\sqrt{3}\cdot\sqrt{2}=5\sqrt{6}$

Приклад$\PageIndex{3}$

Знайдіть довжину відсутньої сторони.

Малюнок$\PageIndex{2}$

Рішення

Використовуйте$x:x:x\sqrt{2}$ співвідношення. $TV=6$тому що вона дорівнює$ST$. Отже,$SV=6 \cdot \sqrt{2}=6\sqrt{2}$.

Приклад$\PageIndex{4}$

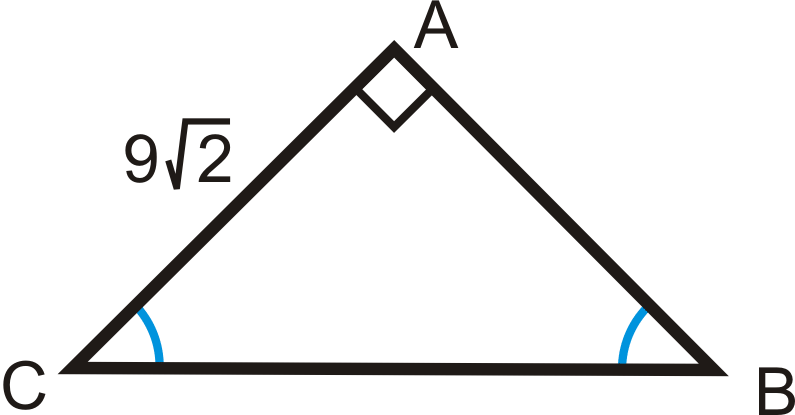
Знайдіть довжину відсутньої сторони.

Малюнок$\PageIndex{3}$

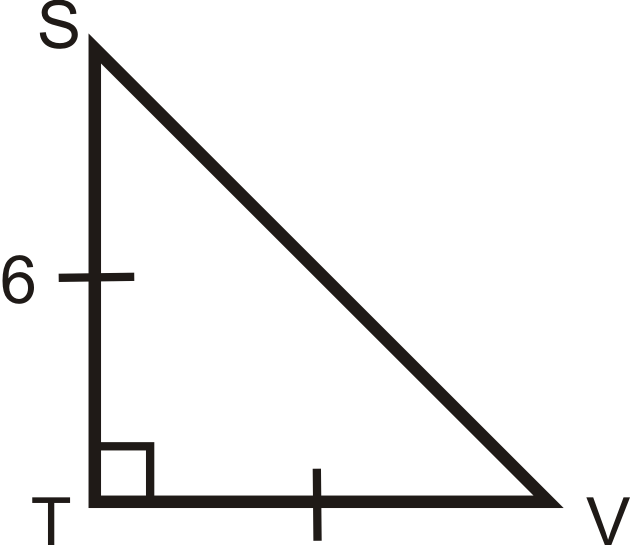
Рішення

Використовуйте$x:x:x\sqrt{2}$ співвідношення. $AB=9\sqrt{2}$тому що вона дорівнює$AC$. Отже,$BC=9\sqrt{2}\cdot\sqrt{2}=9\cdot 2=18$.

Приклад$\PageIndex{5}$

Квадрат має діагональ довжиною 10, які довжини сторін?

Рішення

Намалюйте малюнок.

Малюнок$\PageIndex{4}$

Ми знаємо, що половина квадрата - це трикутник 45-45-90, отже$10=s\sqrt{2}$.

$\begin{aligned} s\sqrt{2}&=10 \\ s&=10\sqrt{2}\cdot \dfrac{\sqrt{2}}{\sqrt{2}}=\dfrac{10\sqrt{2}}{2}=5\sqrt{2} \end{aligned}$

Рецензія

1. У рівнобедреному прямокутному трикутнику, якщо катет дорівнює 4, то гіпотенуза дорівнює __________.
2. У рівнобедреному прямокутному трикутнику, якщо катет дорівнює x, то гіпотенуза дорівнює __________.
3. Квадрат має сторони довжиною 15. Яка довжина діагоналі?
4. Діагональ квадрата дорівнює 22. Яка довжина кожної сторони?

Для питань 5-11 знайдіть довжини відсутніх сторін. Спростити всі радикали.

5. 
   

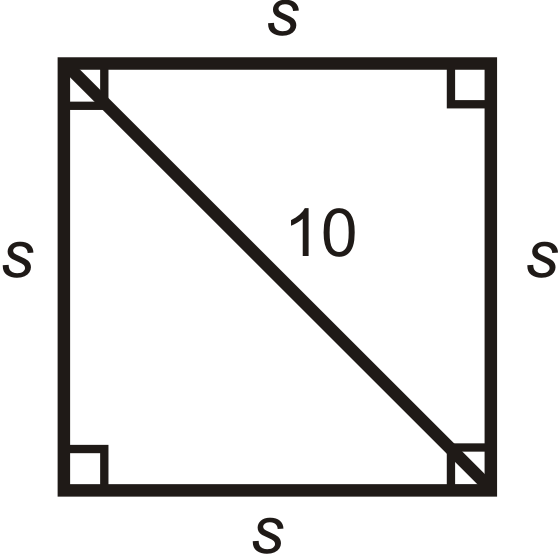
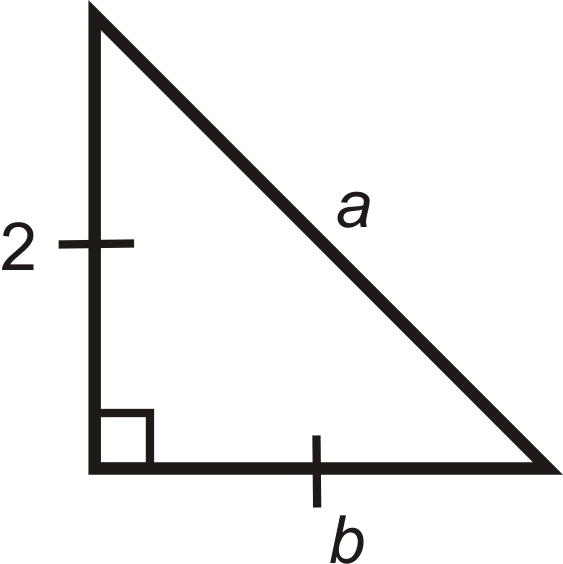
   Малюнок$\PageIndex{5}$

6. 

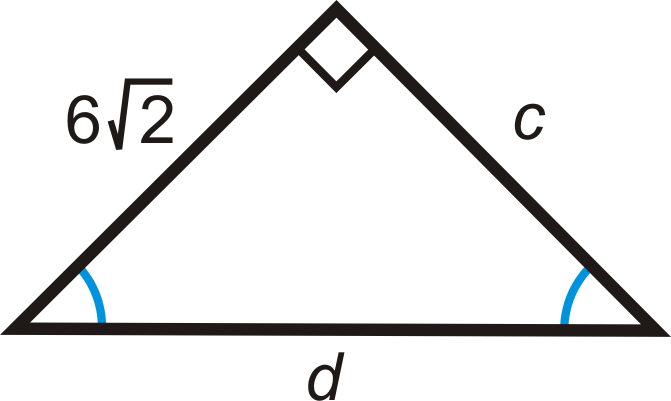
   Малюнок$\PageIndex{6}$

7. 

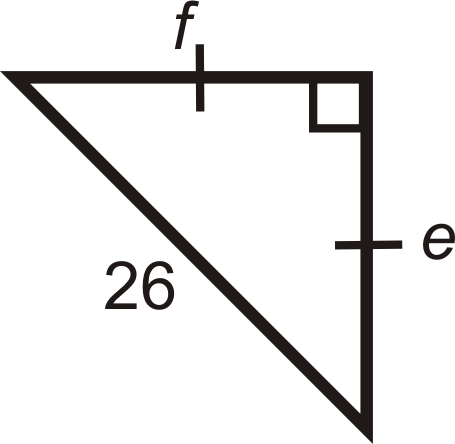
   Малюнок$\PageIndex{7}$

8. 
   

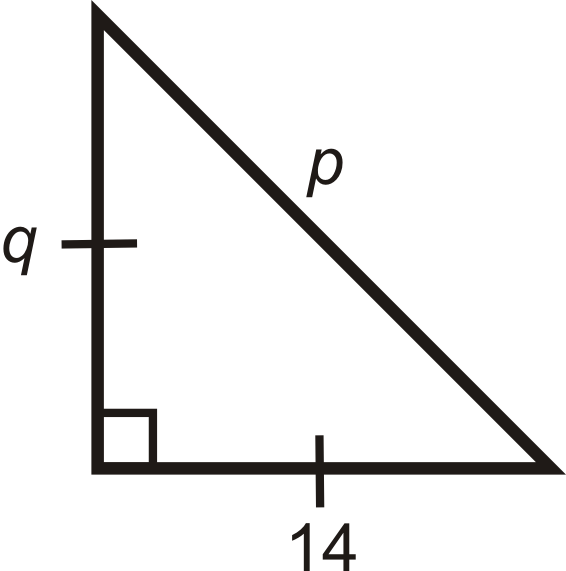
   Малюнок$\PageIndex{8}$

9. 

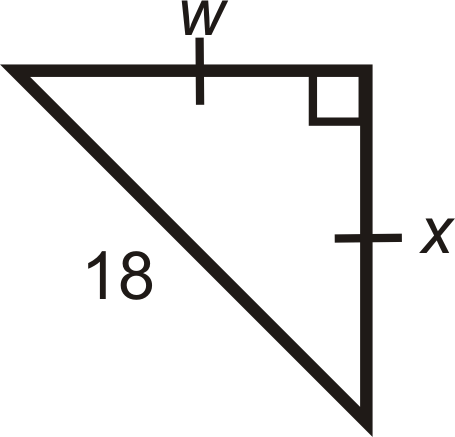
   Малюнок$\PageIndex{9}$

10. 

    Малюнок$\PageIndex{10}$

11. 

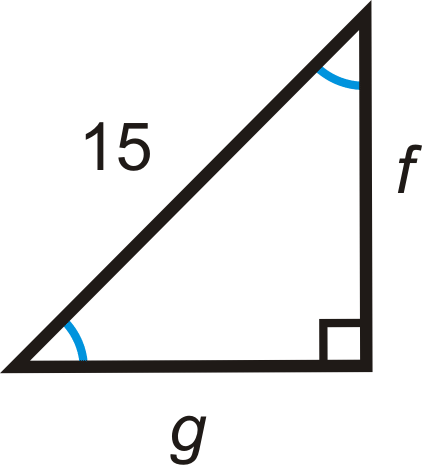
    Малюнок$\PageIndex{11}$

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 8.5.

Ресурси

Лексика

Термін	Визначення
45-45-90 Теорема	Для будь-якого рівнобедреного прямокутного трикутника, якщо катети мають довжину x одиниць, гіпотенуза завжди$x\sqrt{2}$.
45-45-90 Трикутник	Трикутник 45-45-90 - це спеціальний прямокутний трикутник з кутами$45^{\circ}$$45^{\circ}$, і$90^{\circ}$.
Гіпотенуза	Гіпотенуза прямокутного трикутника - найдовша сторона прямокутного трикутника. Вона знаходиться поперек від прямого кута.
Ніжки прямокутного трикутника	Ніжки прямокутного трикутника - це дві коротші сторони прямокутного трикутника. Ноги примикають до прямого кута.
Радикальний	Знак √, або квадратний корінь.

Додаткові ресурси

Інтерактивний елемент

Відео: Розв'язування спеціальних правильних трикутників

Види діяльності: 45-45-90 Прямі трикутники Обговорення Питання

Навчальні посібники: Спеціальні правильні трикутники навчальний посібник

Практика: 45-45-90 Прямі трикутники

Реальний світ: боротьба з війною з наркотиками за допомогою геометрії та спеціальних трикутників