Skip to main content
LibreTexts - Ukrayinska

1.8: Спеціальні правильні трикутники та співвідношення

  1. Last updated
  2. Save as PDF
  • Page ID
    54749

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Властивості 30-60-90 і 45-45-90 трикутників.

    Теорема Піфагора відмінно підходить для знаходження третьої сторони прямокутного трикутника, коли ви вже знаєте дві інші сторони. Є деякі трикутники, такі як трикутники 30-60-90 та 45-45-90, які настільки поширені, що корисно знати бічні співвідношення, не роблячи теорему Піфагора кожного разу. Використання цих шаблонів також дозволяє повністю вирішити відсутні сторони цих спеціальних трикутників, коли ви знаєте лише одну довжину сторони.

    З огляду на 45-45-90 прямокутний трикутник зі сторонами 6 дюймів, 6\(x\) дюймів і дюймів, яке значення\(x\)?

    Спеціальні прямокутні трикутники

    Існує три типи спеціальних прямокутних трикутників, 30-60-90 трикутників, трикутників 45-45-90 та трикутників Піфагора.

    30-60-90 Трикутники

    Прямокутний трикутник 30-60-90 має співвідношення сторін\(x\),\(x\sqrt{3}\),\(2x\).

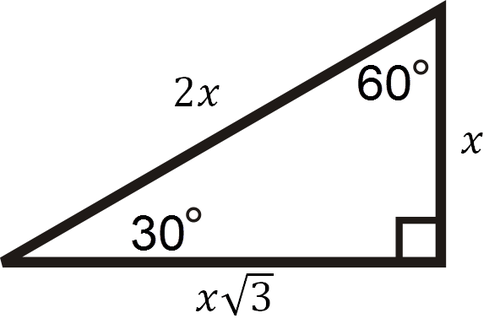
    F-D_895B8BCC4F7A352A2A2B486AFB18DB755900F2CC02AB3060548+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{1}\)

    Підтвердіть теоремою Піфагора:

    \(\begin{aligned} x^2+(x\sqrt{3})^2&=(2x)^2 \\ x^2+3x^2&=4x^2 \\ 4x^2&=4x^2\end{aligned}\)

    45-45-90 Трикутники

    Прямокутний трикутник 45-45-90 має співвідношення сторін\(x, \; x,\; x\sqrt{2}\).

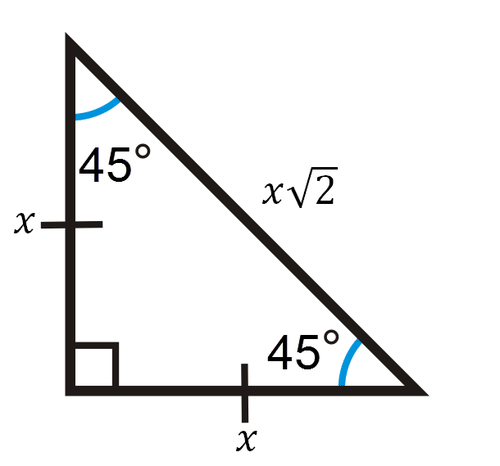
    F-D_48FDDB7ADE9FD2E8B05133FE7E04C7AF925416A07ECDBD6A+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{2}\)

    Підтвердіть теоремою Піфагора:

    \(\begin{aligned} x^2+x^2 &=(x\sqrt{2})^2\\ 2x^2&=2x^2 \end{aligned}\)

    Зверніть увагу, що порядок співвідношення сторін\(x,x\sqrt{3},2x\) і має\(x, x, x\sqrt{2}\) важливе значення, оскільки кожна сторона співвідношення має відповідний кут. У всіх трикутників найменші сторони відповідають найменшим кутам, а найбільші сторони завжди відповідають найбільшим кутам.

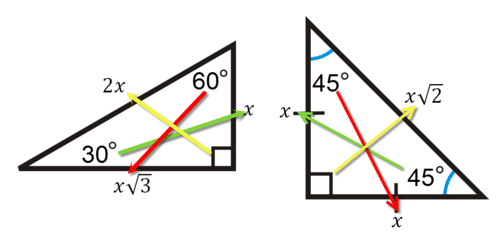
    F-D_9ecfdbcf9a96b1dd5f771a6fd33a662bbe6E35902b20563C4ebcc5+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{3}\)

    Піфагора потрійні трикутники

    Піфагорійська трійка чисел - це спеціальні прямокутні трикутники з цілими сторонами. Хоча кути не є цілими числами, співвідношення сторін дуже корисно знати, оскільки вони з'являються скрізь. Знання цих числових трійок також економить багато часу від повторного виконання теореми Піфагора. Ось кілька прикладів трійок числа Піфагора:

    • 3, 4, 5
    • 5, 12, 13
    • 7, 24, 25
    • 8, 15, 17
    • 9, 40, 41

    Більше трійок числа Піфагора можна знайти шляхом масштабування будь-якого іншого числа Піфагора потрійний. Наприклад:

    \(3,4,5 \rightarrow 6,8,10\)(масштабується в 2 рази)

    Ще більше трійок числа Піфагора можна знайти, взявши будь-яке непарне ціле число, як 11, квадрат його, щоб отримати 121, зменшуючи вдвічі результат, щоб отримати 60,5. Оригінальне число 11 та два числа, які є 0.5 вище і нижче (60 і 61) завжди будуть трійкою числа Піфагора.

    \(11^2+60^2=61^2\)

    Приклад\(\PageIndex{1}\)

    Раніше вас запитали про прямокутний трикутник 45-45-90 зі сторонами 6 дюймів, 6 дюймів і\(x\) дюймів.

    Рішення

    Якщо ви можете розпізнати закономірність для 45-45-90 прямих трикутників, прямокутний трикутник з ніжками 6 дюймів і 6 дюймів має гіпотенузу, яка дорівнює\(6\sqrt{2}\) дюймам. \(x=6\sqrt{2}\).

    Приклад\(\PageIndex{2}\)

    Прямокутний трикутник 30-60-90 має гіпотенузу довжини 10. Які довжини двох інших сторін?

    Рішення

    Гіпотенуза - сторона, протилежна 90. Іноді корисно намалювати малюнок або зробити стіл.

    30

    60

    90

    х

    \(x\sqrt{3}\)

    \(2x\)
       

    10

    З таблиці можна написати дуже малі наступні рівняння для вирішення для відсутніх сторін.

    \(\begin{aligned} 10&=2x\\ x&=5 \\ x\sqrt{3} &=5\sqrt{3}\end{aligned}\)

    Іншими сторонами є\(5\) і\(5\sqrt{3}\).

    Приклад\(\PageIndex{3}\)

    Прямокутний трикутник 30-60-90 має довжину сторони 18 дюймів, що відповідає 60 градусам. Які довжини двох інших сторін?

    Рішення

    Складіть таблицю з співвідношеннями сторін і наданою інформацією, потім запишіть рівняння і вирішіть для відсутніх довжин сторін.

    30

    60

    90

    х

    \(x\sqrt{3}\)

    \(2x\)
     

    18

    		  

    \(\begin{aligned}18&=x\sqrt{3} \\ \dfrac{18}{\sqrt{3}}&=x \\ x&=18\sqrt{3}=18\sqrt{3} \cdot \dfrac{\sqrt{3}}{\sqrt{3}}=18\dfrac{\sqrt{3}}{3}=6\sqrt{3}\\ x&=6\sqrt{3}\end{aligned}\)

    Зверніть увагу, що потрібно раціоналізувати знаменники.

    Тепер використовуйте обчислене\(x\) значення для вирішення\(2x\).

    \(\begin{aligned} 2x&=2(6\sqrt{3}) \\ 2x&=12\sqrt{3} \end{aligned}\)

    Іншими сторонами є\(6\sqrt{3}\) і\(12\sqrt{3}\).

    Приклад\(\PageIndex{4}\)

    Використовуючи свої знання про спеціальні співвідношення прямокутного трикутника, вирішуйте для відсутніх сторін прямокутного трикутника.

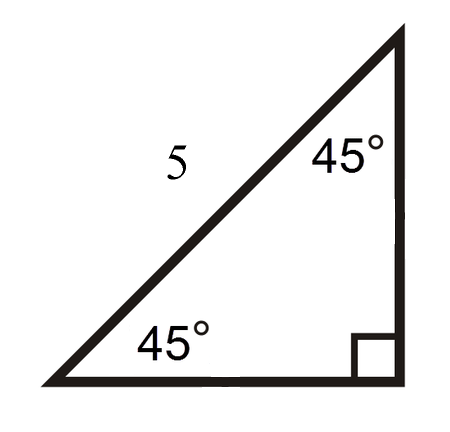
    F-D_09280BE2B657F2EEB3157 BEBFD1A8C233292A14E0535866E3E95B85F+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{4}\)

    Рішення

    Інші сторони - кожна\(\dfrac{5\sqrt{2}}{2}\).

    45

    45

    90

    \(x\)

    \(x\)

    \(x\sqrt{2}\)
       

    5

    \(\begin{aligned} x\sqrt{2}&=5 \\ x&=\dfrac{5}{\sqrt{2}} \cdot \dfrac{\sqrt{2}}{\sqrt{2}}=\dfrac{5\sqrt{2}}{2} \end{aligned}\)

    Інші сторони - кожна\(5\dfrac{\sqrt{2}}{2}\).

    Приклад\(\PageIndex{1}\)

    Використовуючи свої знання про спеціальні співвідношення прямокутного трикутника, вирішуйте для відсутніх сторін прямокутного трикутника.

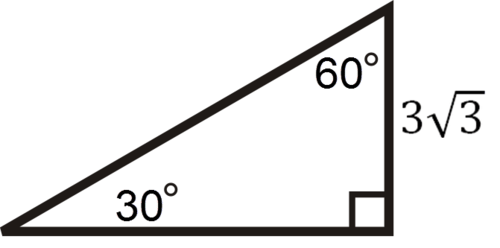
    F-D_BCA094C0BBCC4034bb4cd3d003dc17084d8A5d5d5218095f3014CC2cc6+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{5}\)

    Рішення

    Іншими сторонами є\(9\) і\(6\sqrt{3}\).

    30

    60

    90

    \(x\)

    \(x\sqrt{3}\)

    \(2x\)

    \(3\sqrt{3}\)

    		    

    \(\begin{aligned} x&=3\sqrt{3} \\ 2x&=6\sqrt{3} \\ x\sqrt{3}&=3\sqrt{3} \cdot \sqrt{3}=9 \end{aligned}\)

    Іншими сторонами є\(9\) і\(6\sqrt{3}\).

    Рецензія

    Для 1-4 знайдіть відсутні сторони трикутника 45-45-90 на основі інформації, наведеної в кожному рядку.

    Номер проблеми

    Сторона протилежна\(45^{\circ}\)

    Сторона протилежна\(45^{\circ}\)

    Сторона протилежна\(90^{\circ}\)

    1.

    3

    		    

    2.

    		  

    7.2

    		  

    3.

    		    

    16

    4.

    		 \(5\sqrt{2}\)    

    Для 5-8 знайдіть відсутні сторони трикутника 30-60-90 на основі інформації, наведеної в кожному ряду.

    Номер проблеми

    Сторона протилежна\(30^{\circ}\)

    Сторона протилежна\(60^{\circ}\)

    Сторона протилежна\(90^{\circ}\)

    5.

    		 \(3\sqrt{2}\)    

    6.

    		  

    4

    		  

    7.

    		    

    15

    8.

    		     \(12\sqrt{3}\)

    Використовуйте картинку нижче для 9-11.

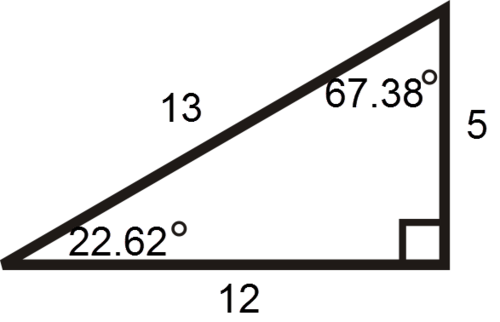
    F-D_292CBB695797564417FCF424685 EAF1A7E8549CE5C914649FC84D5D+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{6}\)
    1. Який кут відповідає стороні, яка дорівнює 12 одиницям?
    2. Яка сторона відповідає прямому куту?
    3. Який кут відповідає стороні, яка дорівнює 5 одиницям?
    4. Прямокутний трикутник має кут\(\dfrac{\pi}{6}\) радіанів і гіпотенузу 20 дюймів. Які довжини двох інших сторін трикутника?
    5. Трикутник має два кути, які вимірюють\(\dfrac{\pi}{4}\) радіани. Найдовша сторона - 3 дюйма завдовжки. Які довжини двох інших сторін?

    Для 14-19 перевірте число Піфагора Потрійний за допомогою теореми Піфагора.

    1. 3, 4, 5
    2. 5, 12, 13
    3. 7, 24, 25
    4. 8, 15, 17
    5. 9, 40, 41
    6. 6, 8, 10
    7. Знайдіть інший Піфагорійський номер Потрійний за допомогою методу, поясненого для знаходження «11, 60, 61».

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 4.3.

    Лексика

    Термін Визначення
    30-60-90 Трикутник Трикутник 30-60-90 - це спеціальний прямокутний трикутник з кутами\(30^{\circ}\)\(60^{\circ}\), і\(90^{\circ}\).
    45-45-90 Трикутник Трикутник 45-45-90 - це спеціальний прямокутний трикутник з кутами\(45^{\circ}\)\(45^{\circ}\), і\(90^{\circ}\).
    Піфагорейське число потрійне Піфагорійська трійка - це набір з трьох цілих чисел a, b і c, які задовольняють теоремі Піфагора,\(a^2+b^2=c^2\).
    Теорема Піфагора Теорема Піфагора - це математична залежність між сторонами прямокутного трикутника, задана\(a^2+b^2=c^2\), де a і b - катети трикутника, а c - гіпотенуза трикутника.