1.1: Теорема Піфагора
- Page ID
- 54750
Відкрийте, геометрично доведіть та застосуйте теорему Піфагора.
Довжини сторін трикутника з використанням теореми Піфагора
Ви тільки що підписалися, щоб бути помічником архітектора в новому офісі в центрі міста. Вас просять намалювати масштабну модель скульптури для бізнес-площі. Скульптура має великий трикутний шматок, де один з кутів між сторонами становить дев'яносто градусів. Цей тип трикутника називається «прямокутним трикутником». Архітектор, над яким ви працюєте, входить в кімнату і говорить вам, що сторони трикутника, які утворюють прямий кут, становлять 9 футів і 12 футів. Чи можете ви сказати, як довго третя сторона?
Пошук довжини сторін трикутника з використанням теореми Піфагора
З геометрії нагадаємо, що теорема Піфагора - це\(a^2+b^2=c^2\) де\(a\) і\(b\) є катетами прямокутного трикутника і\(c\) є гіпотенузою. Також сторона, протилежна куту, є нижнім регістрам, а кут - верхній регістр. Наприклад, кут\(A\) протилежної сторони\(a\).
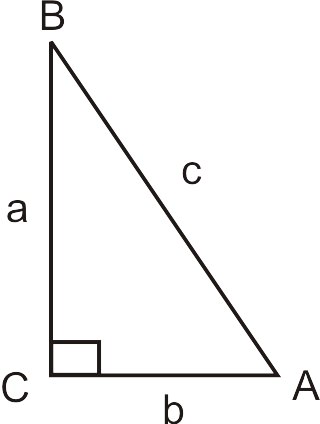
Теорема Піфагора використовується для розв'язання сторін прямокутного трикутника.
Використання теореми Піфагора
1.
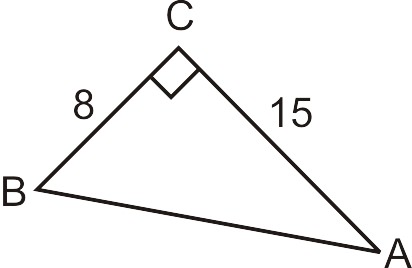
\(a=8\),\(b=15\), нам потрібно знайти гіпотенузу.
\(\begin{aligned} 8^2+15^2&=c^2 \\ 64+225&=c^2 \\ 289&=c^2 \\ 17&=c \end{aligned}\)
Зверніть увагу, ми не включаємо -17 як рішення, оскільки від'ємне число не може бути стороною трикутника.
2.
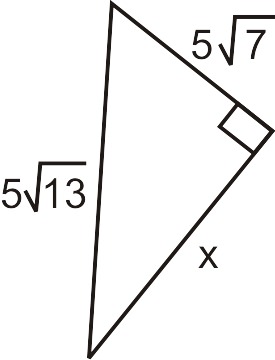
Використовуйте теорему Піфагора, щоб знайти відсутню ніжку.
\(\begin{aligned} (5\sqrt{7})^2+x^2&=(5\sqrt{13})^2 \\ 25\cdot 7+x^2&=25\cdot 13 \\ 175+x^2&=325 \\ x^2&=150 \\ x&=5\sqrt{6}\end{aligned}\)
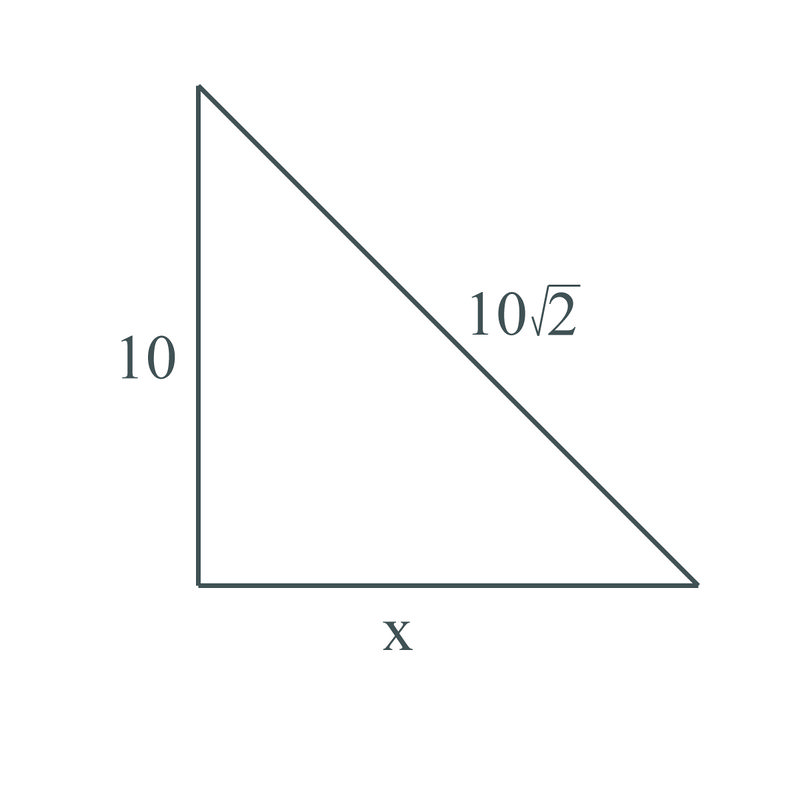
3. Використовуйте теорему Піфагора, щоб знайти відсутню ніжку в трикутнику вище.
\(\begin{aligned} 10^2+x^2&=(10\sqrt{2})^2 \\ 100+x^2&=100\cdot 2 \\ 100+x^2&=100 \\ x^2&=100 \\ x&=10 \end{aligned}\)
Раніше вам поставили проблему з проханням намалювати масштабну модель скульптури для бізнес-площі.
З вашим знанням теореми Піфагора, ви можете побачити, що трикутник має сторони з довжиною 9 футів і 12 футів. Ви працюєте, щоб знайти гіпотенузу:
Рішення
\(\begin{aligned} a^2+b^2&=c^2 \\ 9^2+12^2&=c^2 \\ 81+144&=c^2 \\ 225&=c^2 \\ (\sqrt{225})&=15=c \end{aligned}\)
Зважаючи на те, що довжина третьої сторони трикутника становить 15 футів, ви можете легко побудувати свою масштабну модель.
Використовуйте теорему Піфагора, щоб знайти відсутню сторону наступного трикутника:
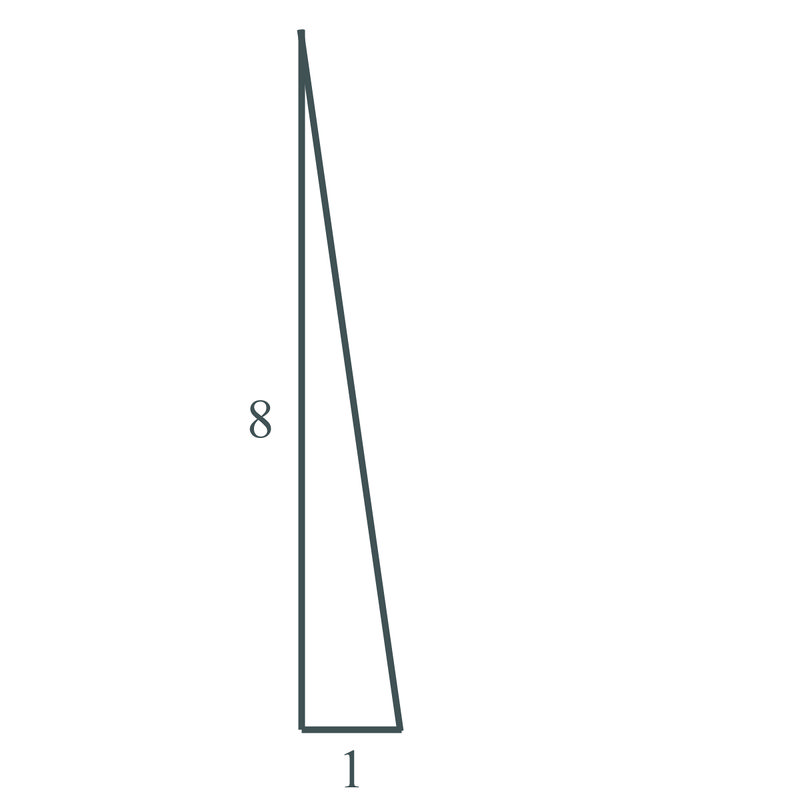
Рішення
\(a=1\),\(b=8\), нам потрібно знайти гіпотенузу.
\(\begin{aligned} 1^2+8^2&=c^2 \\ 1+64&=c^2 \\ 65&=c^2 \\ \sqrt{65}&=c\end{aligned}\)
Використовуйте теорему Піфагора, щоб знайти відсутню сторону наступного трикутника:
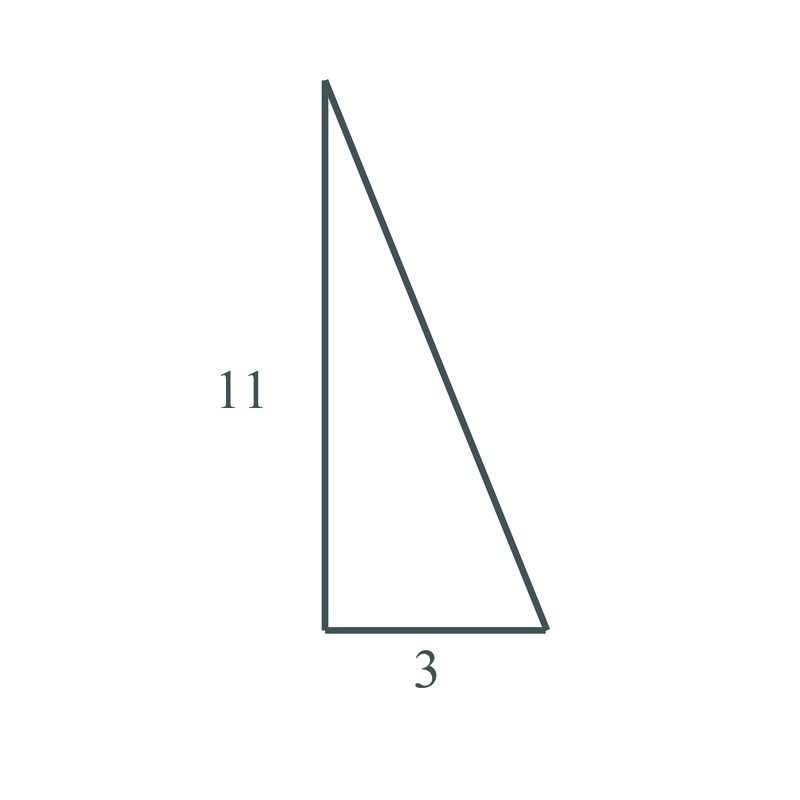
Рішення
\(a=3\),\(b=11\), нам потрібно знайти довжину сторони c, гіпотенузи.
\(\begin{aligned} 3^2+11^2&=c^2 \\ 9+121&=c^2 \\ 130&=c^2 \\ \sqrt{130}&=c\end{aligned}\)
Знайдіть відсутню сторону прямокутного трикутника внизу. Залиште відповідь в найпростішій радикальній формі.
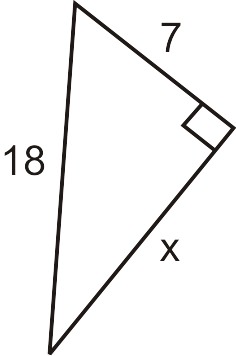
Рішення
\(a=7\)\(c=18\),, Нам потрібно знайти довжину сторони b.
\(\begin{aligned}7^2+b^2=18^2 \\ 49+b^2=18^2 \\ 324−49=b^2 \\ 275=b^2 \\ \sqrt{275}=b \end{aligned}\)
Рецензія
Знайдіть відсутні сторони правильних трикутників. Залишайте відповіді в найпростішій радикальній формі.
- Якщо катети прямокутного трикутника 3 і 4, то гіпотенуза дорівнює _____________.
- Якщо катети прямокутного трикутника - 6 і 8, то гіпотенуза дорівнює _____________.
- Якщо катети прямокутного трикутника 5 і 12, то гіпотенуза дорівнює _____________.
- Якщо сторони квадрата довжиною 6, то діагональ - _____________.
- Якщо сторін квадрата 9, то діагональ - _____________.
- Якщо сторони квадрата є\(x\), то діагональ - _____________.
- Якщо катети прямокутного трикутника 3 і 7, то гіпотенуза дорівнює _____________.
- Якщо катети прямокутного трикутника дорівнюють\(2\sqrt{5}\) і 6, то гіпотенуза дорівнює _____________.
- Якщо один катет прямокутного трикутника дорівнює 4, а гіпотенуза - 8, то інший катет _____________.
- Якщо один катет прямокутного трикутника дорівнює 10, а гіпотенуза - 15, то інший катет _____________.
- Якщо один катет прямокутного трикутника є\(4\sqrt{7}\)\(10\sqrt{6}\), а гіпотенуза - то інший катет _____________.
- Якщо катети прямокутного трикутника дорівнюють x і y, то гіпотенуза дорівнює ____________.
Доказ теореми Піфагора
Скористайтеся зображенням нижче, щоб відповісти на наступні питання.

- Знайти площу квадрата на зображенні зі сторонами (a+b).
- Знайти суму площ квадрата зі сторонами c і правильних трикутників з ніжками a і b.
- Поясніть, чому області, знайдені в попередніх двох проблемах, повинні мати однакове значення. Потім встановіть вирази рівні один одному і спростіть, щоб отримати теорему Піфагора.
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 1.1.
Лексика
| Термін | Визначення |
|---|---|
| Теорема Піфагора | Теорема Піфагора - це математична залежність між сторонами прямокутного трикутника, задана\(a^2+b^2=c^2\), де a і b - катети трикутника і\(c\) є гіпотенузою трикутника. |