1.1:1.1 Функціональні сім'ї

Функції бувають різних форм. Деякі дуже тісно пов'язані між собою, а інші дуже різні, але часто плутають. Наприклад, в чому різниця між$x^{2}$ і$2^{x}$? Вони обидва мають$x$ і 2, і вони обидва рівні 4 коли$x=2$, але один в кінцевому підсумку стає набагато більше, ніж інший.

Сімейства функцій

Якщо математики - кухарі, то сімейства функцій є їх інгредієнтами. Кожне сімейство функцій має свій колорит і індивідуальність. Перш ніж навчитися комбінувати функції для створення нескінченної кількості потенційних моделей, необхідно отримати чітке уявлення про назву кожного сімейства функцій і як воно діє.

Функція ідентичності:$f(x)=x$

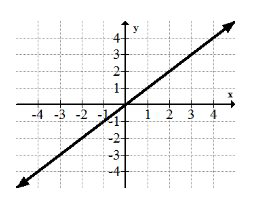
Функція ідентичності є найпростішою функцією, а всі прямі є перетвореннями сімейства функцій ідентичності.

Функція квадратури:$f(x)=x^{2}$

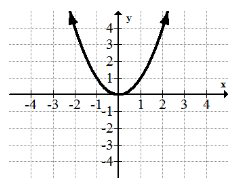
Функція квадратури (квадратична функція) прийнято називати параболою і корисна для моделювання руху падаючих предметів. Всі параболи є перетвореннями цієї квадратної функції.

Функція кубінгу:$f(x)=x^{3}$

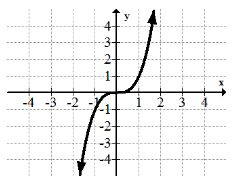
Функція кубінгу має інший вид симетрії, ніж функція квадратури. Оскільки обсяг вимірюється в кубічних одиницях, багато додатків фізики використовують кубічну функцію.

Функція квадратного кореня:$f(x)=\sqrt{x}=x^{\frac{1}{2}}$

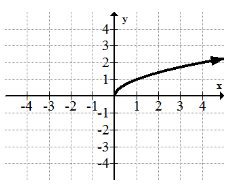
Функція квадратного кореня не визначена над усіма дійсними числами. Він вводить можливість комплексних чисел, а також тісно пов'язаний з функцією квадратування.

Зворотна функція:$f(x)=x^{-1}=\frac{1}{x}$

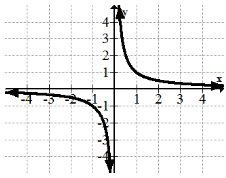
Реципрокна функція також відома як гіпербола і раціональна функція. Він має дві частини, які роз'єднані і не визначені на нулі. Прості електричні схеми моделюються з зворотною функцією.

Поки що всі функції можуть бути згруповані разом у ще більшу сімейство функцій, яка називається сімейством функцій влади.

Сімейство функцій живлення:$f(x)=c x^{a}$

Сімейство функцій харчування має два параметри. Параметр$c$ являє собою вертикальний масштабний коефіцієнт. Параметр$a$ керує всім, що стосується форми. Причина, чому всі функції досі є підмножинами більшого сімейства функцій потужності, полягає в тому, що вони відрізняються лише своїм значенням$a$. Сімейство функцій живлення також показує вам, що існує нескінченна кількість інших функцій, таких як квартики$\left(f(x)=x^{4}\right)$ та квінтики$\left(f(x)=x^{5}\right)$, які насправді не потребують цілої категорії. Сімейство силових функцій може бути розширено для створення поліномів і раціональних функцій.

Сімейство експоненціальних функцій:$f(x)=e^{x}$

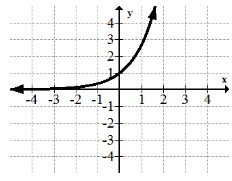
Сімейство експоненціальних функцій є однією з перших функцій, які ви бачите, де не$x$ є базою показника. Ця функція з часом зростає набагато швидше, ніж будь-яка силова функція. $f(x)=2^{x}$є дуже поширеною експоненціальною функцією, а також. Багато програм, таких як біологія та фінанси, вимагають використання експоненціального зростання.

Функція логарифма:$f(x)=\ln x$

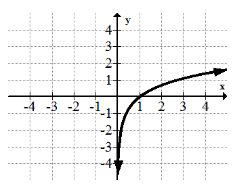
Логарифмічна функція тісно пов'язана з сімейством експоненціальних функцій. Багато людей плутають графік функції log з функцією квадратного кореня. Ретельний аналіз покаже кілька важливих відмінностей. Функція журналу є основою для шкали Ріхтера, яка полягає в тому, як вимірюються землетруси.

Сімейство періодичних функцій:$f(x)=\sin x$

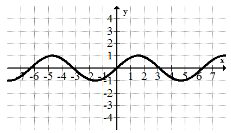
Синусоїдальний графік є однією з багатьох періодичних функцій. Періодичний відноситься до того, що синусоїда повторює цикл кожен проміжок часу. Періодичні функції надзвичайно важливі для моделювання припливів і інших явищ реального світу.

Функція абсолютного значення:$f(x)=|x|$

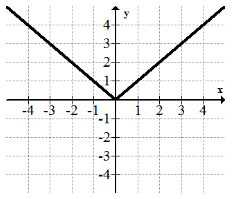
Функція абсолютного значення - одна з небагатьох основних функцій, яка не є повністю гладкою.

Логістична функція:$f(x)=\frac{1}{1+e^{-x}}$

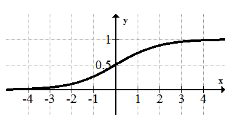
Логістична функція являє собою поєднання експоненціальної функції і зворотної функції. Ця крива є дуже потужною, оскільки вона моделює зростання населення, де максимальна чисельність населення обмежена екологічними ресурсами.

Приклади

Приклад 1

Раніше вам давали задачу про порівняння$x^{2}$ і$2^{x}$. Хоча$x^{2}$ і$2^{x}$ мають схожі інгредієнти, вони мають дуже різні графічні особливості. Функція квадрата симетрична щодо лінії,$x=0$ тоді як експоненціальна функція - ні. Коли$x=0$, функція квадратизації має висоту нуля, а експоненціальна функція має висоту одиниці. Квадратна функція має нахил, який стає крутішим, коли$x$ виходить далі від початку, тоді як експоненціальна функція вирівнюється, коли$x$ стає дуже маленькою. Всі ці відмінності важливі і не очевидні на перший погляд.

Приклад 2

$y=x$$y=e^{x}$,$y=\frac{1}{1+e^{-x}} .$ Деякі функції, які близькі, але не зовсім:$y=x^{3}$,$y=\sqrt{x}$

Приклад 3

Порівняйте та порівняйте графіки двох функцій:

$f(x)=\ln x$і$h(x)=\sqrt{x}$

Подібність: Обидві функції збільшуються без прив'язки, оскільки$x$ стають більшими. Обидві функції не визначені для від'ємних чисел.

Відмінності: Функція журналу наближається до негативної нескінченності як$x$ до 0. Функція квадратного кореня, з іншого боку, просто закінчується в точці (0,0).

Приклад 4

Опишіть симетрію серед сімейств функцій, розглянутих у цьому понятті. Розглянемо як симетрію відображення, так і обертальну симетрію.

Деякі сімейства функцій мають відбивну симетрію з собою:

$y=x$,$y=x^{2}$,$y=\frac{1}{x}$,$y=|x|$

Деякі сімейства функцій обертально симетричні:

$y=x$,$y=x^{3}$,$y=\frac{1}{x}$,$y=\sin x$,$y=\frac{1}{1+e^{-x}}$

Деякі пари сімейств функцій є повним або частковим відображенням інших сімейств функцій:

$y=x^{2}$,$y=\sqrt{x}$

$y=e^{x}$,$y=\ln x$

Рецензія

Для 1-10 намалюйте графік функції з пам'яті.

1. $y=e^{x}$

2. $y=\ln (x)$

3. $y=\sin (x)$

4. $y=x^{2}$

5. $y=|x|$

6. $y=\frac{1}{x}$

7. $y=\frac{1}{1+e^{-x}}$

8. $y=\sqrt{x}$

9. $y=x^{3}$

10. $y=x$

11. Яка функція не визначена при 0? Чому?

12. Які функції обмежені нижче, але не вище??

13. Які відмінності між$y=x^{2}$ і$y=x^{3}$?

14. Що таке подібність між$y=e^{x}$ і$y=\ln (x)$?

15. Поясніть$y=\sqrt{x}$, чому не визначено для всіх значень$x$.