1.2:1.2 Графічні перетворення

Основні функції потужні, але вони надзвичайно обмежені, поки ви не зможете змінити їх відповідно до будь-якої ситуації. Перетворення означає, що ви можете змінити рівняння базової функції шляхом додавання, віднімання та/або множення на константи і таким чином викликати відповідну зміну графіку. Які наслідки наступних перетворень?

1. $f(x) \rightarrow f(x+3)$
2. $h(x) \rightarrow h(x)-5$
3. $g(x) \rightarrow-g(2 x)$
4. $j(x) \rightarrow j\left(-\frac{x}{2}\right)$

Трансформація функцій

Функція - це правило, яке приймає будь-який вхід$x$ і дає певний висновок. Коли ви використовуєте літери$f$ типу$g$$h$, або$j$ для опису правила, це називається позначенням функції. Для того, щоб інтерпретувати, який вплив матиме алгебраїчна зміна рівняння на графіку, важливо вміти читати ці зміни в загальних позначеннях функцій, а потім застосовувати їх до конкретних випадків.

При перетворенні функції можна перетворити аргумент (частина всередині дужок з$x$), або саму функцію. Існує два способи лінійного перетворення аргументу. Ви можете помножити$x$ на константу та/або додати константу$x$ до показаного нижче:

$f(x) \rightarrow f(b x+c)$

Сама функція також може лінійно трансформуватися тими ж способами:

$f(x) \rightarrow a f(x)+d$

Кожна з букв$a$,,$b$$c$, і$d$ відповідає дуже конкретній зміні. Деякі з цих змін є простими, тоді як інші можуть бути протилежними тому, що ви можете очікувати.

• $a$являє собою вертикальну розтяжку. Якщо$a$ негативний, також є відображення поперек$x$ осі.
• $d$являє собою вертикальний зсув. Якщо$d$ позитивний, то зрушення вгору. Якщо$d$ негативний, то зсув - вниз.

При перетворенні аргументу функції справи йдуть складніше.

• $\frac{1}{b}$являє собою горизонтальну розтяжку. Якщо$b$ негативний, також є відображення поперек$y$ осі.
• $c$являє собою горизонтальний зсув. Якщо$c$ позитивний, то зсув - вліво. Якщо$c$ негативний, то зсув - вправо. Зверніть увагу, що це протилежне тому, що більшість людей думають спочатку.

Найскладніша частина з перетворенням аргументу функції - це порядок, в якому ви виконуєте перетворення. Часто має сенс застосувати перетворення до певної функції, яка відома, а потім описати перетворення, яке ви бачите.

На графіку нижче показано перетворення,$f(x) \rightarrow f(3 x-6)$ застосоване до простої параболи:

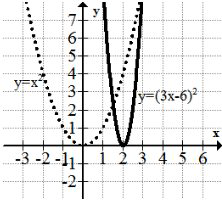
Зрозуміло, що графік вужчий і праворуч, але для того, щоб бути конкретним, ви повинні придивитися ближче. По-перше, зверніть увагу, що перетворення повністю знаходиться в межах аргументу функції. Це впливає тільки на горизонтальні значення. Це означає, що, хоча графік здається, що він розтягнутий вертикально, ви повинні тримати свою перспективу зосередженою на горизонтальному стисненні.

Подивіться уважно на вершину параболи. Він перемістився вправо дві одиниці. Це пов'язано з тим, що спочатку весь графік був повністю зміщений вправо 6 одиниць. Потім функція була горизонтально стиснута коефіцієнтом 3, що означає, що точка (6, 0) стала (2, 0), а$x$ значення кожної іншої точки також стиснулося на коефіцієнт 3 до лінії$x=0$. Цей метод не є інтуїтивним, оскільки вимагає читання перетворень назад (протилежне тому, як вказує порядок операцій).

Крім того, аргумент може бути врахований і кожен компонент перетворення представить себе.

$f(3(x-2))$

Цього разу розтягнення відбувається від центру перетвореного графіка, а не від початку. Цей метод в кінцевому рахунку є кращим методом.

Так чи інакше, це горизонтальне стиснення в 3 рази і горизонтальний зсув вправо на 2 одиниці.

Тепер візьміть перетворення$f(x) \rightarrow-\frac{1}{4} f(x)+3 .$ Він описує вертикальне розтягнення на коефіцієнт відображення над$x$ віссю, і вертикальний зсув на 3 одиниці вгору.$\frac{1}{4},$ На відміну від того, що ви бачили вище, порядок перетворень для чогось поза аргументом - це безпосередньо те, що диктує порядок операцій.

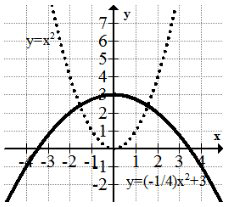
По-перше, парабола відбивається над$x$ віссю і стискається вертикально, щоб вона виглядала ширше. Потім кожну точку переміщують вгору на 3 одиниці.

Трансформація$f(x) \rightarrow-3 f\left(-\frac{1}{2} x-1\right)+1$ містить всі можливі перетворення. Горизонтальна і вертикальна компоненти не взаємодіють один з одним, тому ваш опис перетворення може починатися з будь-якого компонента. Тут почнемо з опису вертикальних складових перетворення:

По-перше, відбувається відображення поперек$x$ осі і вертикальне розтягнення в 3 рази. Потім відбувається вертикальний зсув вгору на 1 одиницю. Нижче наведено зображення неспецифічної функції, що проходить через вертикальні перетворення.

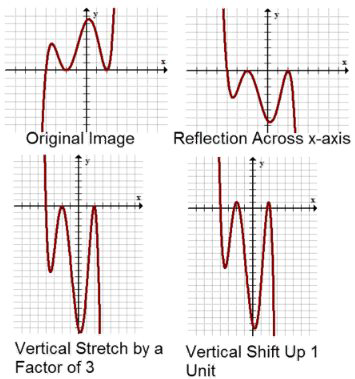
Для того щоб з'ясувати горизонтальні складові перетворення, почніть з факторингу внутрішньої частини дужок (аргумент):

$f\left(-\frac{1}{2} x-1\right)=f\left(-\frac{1}{2}(x+2)\right)$

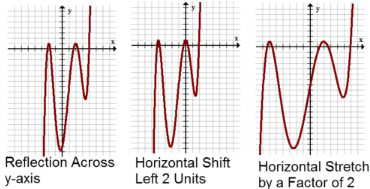
Факторинг виявляє відображення поперек$y$ осі, горизонтальний зсув вліво на 2 одиниці і горизонтальний розтяг на коефіцієнт$2 .$ Нижче - це зображення тієї ж функції, що проходить через горизонтальні перетворення.

Приклади

Приклад 1

Раніше вам давали задачу про наслідки наступних перетворень:

$f(x) \rightarrow f(x+3)$

Це перетворення зміщує весь графік вліво на 3 одиниці. Поширеною помилкою є зміщення праворуч, оскільки три позитивні.

$h(x) \rightarrow h(x)-5$

Це перетворення зміщує весь графік вниз на 5 одиниць.

$g(x) \rightarrow-g(2 x)$

Це перетворення являє собою вертикальне відображення по осі x і горизонтальне стиснення в 2 рази.

$j(x)=j\left(-\frac{x}{2}\right)$

Це перетворення є горизонтальним відображенням поперек$y$ осі та горизонтальним розтягуванням на коефіцієнт$2 .$ Поширена помилка полягає в тому, щоб побачити$\frac{1}{2}$ і вважати, що$x$ значення будуть вдвічі менше, що є горизонтальним стисненням. Однак значення\ x\) повинні бути вдвічі більшими, щоб протидіяти цьому фактору$\frac{1}{2}$

Приклад 2

Опишіть наступну трансформацію словами:$g(x) \rightarrow 2 g(-x)$

Вертикальне розтягування в 2 рази і відображення поперек$y$ осі.

Приклад 3

Опишіть трансформацію, яка$h(x)$ змінилася б наступними способами:

• Вертикальне стиснення в 3 рази.
• Вертикальний зсув вниз на 4 одиниці.
• Горизонтальний зсув вправо 5 од.

$\frac{1}{3} h(x-5)-4$

Приклад 4

Опишіть трансформацію, яка$f(x)$ змінилася б наступними способами:

• Горизонтальне розтягування в 4 рази і горизонтальне зсув на 3 одиниці вправо.
• Вертикальне відображення поперек$x$ осі і зсув вниз на 2 одиниці.

$-f\left(\frac{1}{4}(x-3)\right)-2$або$-f\left(\frac{1}{4} x-\frac{3}{4}\right)-2$

Рецензія

Опишіть наступні перетворення словами.

1. $g(x) \rightarrow-g(-x)$
2. $f(x) \rightarrow-f(x+3)$
3. $h(x) \rightarrow h(x+1)-2$
4. $j(x) \rightarrow j(-x+3)$
5. $k(x) \rightarrow-k(2 x)$
6. $f(x) \rightarrow 4 f\left(\frac{1}{2} x+1\right)$
7. $g(x) \rightarrow-3 g(x-2)-2$
8. $h(x) \rightarrow 5 h(x+1)$

9. Опишіть трансформацію, яка$h(x)$ змінилася б наступними
способами:

• Вертикальна розтяжка в 2 рази
• Вертикальний зсув вгору на 3 одиниці.
• Горизонтальний зсув вправо 2 од.

10. Опишіть трансформацію, яка$f(x)$ змінилася б наступними
способами:

• Вертикальне відображення по осі x.
• Вертикальний зсув вниз на 1 одиницю.
• Горизонтальний зсув вліво 2 од.

11. Опишіть трансформацію, яка$g(x)$ змінилася б наступними
способами:

• Вертикальне стиснення в 4 рази.
• Відображення поперек$y$ осі.

12. Опишіть трансформацію, яка$j(x)$ змінилася б наступними
способами:

• Горизонтальне стиснення в 3 рази.
• Вертикальний зсув вгору на 3 одиниці.
• Горизонтальний зсув вправо 2 од.

13. Опишіть трансформацію, яка$k(x)$ змінилася б наступними
способами:

• Горизонтальна розтяжка в 4 рази.
• Вертикальний зсув вгору на 3 одиниці.
• Горизонтальний зсув вліво 1 од.

14. Опишіть трансформацію, яка$h(x)$ змінилася б наступними
способами:

• Вертикальне стиснення в 2 рази.
• Горизонтальний зсув вправо 3 од.
• Відображення поперек$y$ осі.

15. Опишіть трансформацію, яка$f(x)$ змінилася б наступними
способами:

• Вертикальна розтяжка в 5 разів.
• Відображення поперек$x$ осі