2.4: Основні тригонометричні межі

Тригонометричні функції можуть бути складовою виразу і, отже, підлягати граничному процесу. Чи вважаєте ви, що періодичний характер цих функцій та обмежений або нескінченний діапазон окремих тригонометричних функцій ускладнить оцінку меж за участю цих функцій?

---

Межі з тригонометричними функціями

Граничні правила, представлені в попередніх концепціях, пропонують деякі, але не всі, інструменти для оцінки меж за участю тригонометричних функцій.

Давайте знайдемо наступні межі:

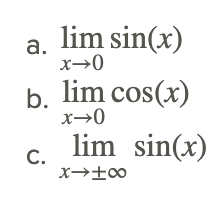
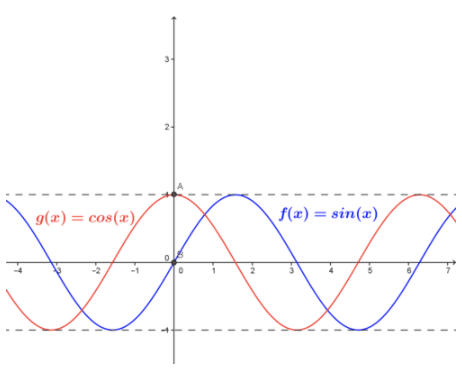
Ми можемо знайти ці межі, оцінюючи функцію як х наближається до 0 зліва і справа, тобто шляхом оцінки двох односторонніх меж. Графіки та таблиці значень наведені нижче.

CC ЗА NC-SA

x (читати)	-0,001	-0,0001	0	0,0001	0,001
гріх (х)	-0,001	-0,0001	0	0,0001	0,001
кос (х)	0.999	0,999	1	0,999	0.999

Огляд наведеного нижче графіка та таблиці значень поблизу x=0 вказує на те, що:

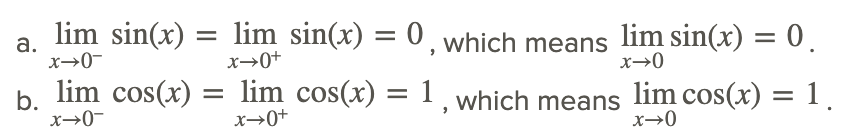
Зверніть увагу, що ліміти можна знайти за допомогою прямої підміни.

3. Оскільки sin (x) є періодичною функцією, оскільки x стає більшим (меншим) і більшим (меншим), його значення коливатиметься між 1 і -1 і ніколи не осідає на одне значення. Тому можна сказати, що
   
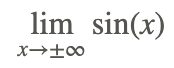
   не існує.

Ми можемо узагальнити та розширити наведені вище висновки та представити наступні властивості:

Граничні властивості базових тригонометричних функцій

• Обмеження як x → a для будь-якого реального a:

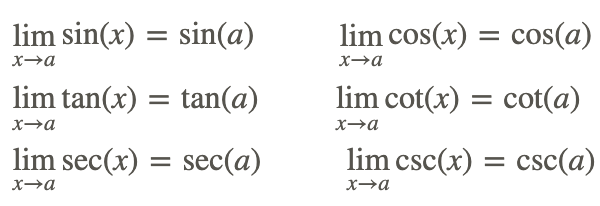
• Обмеження як x → ± ∞:

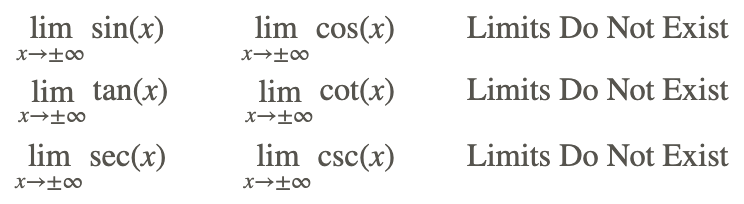
Давайте знайдемо

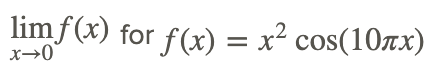
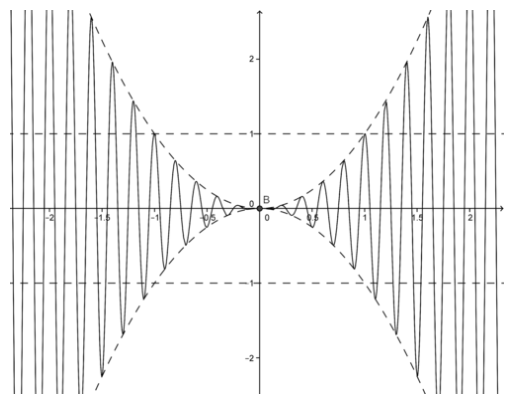
Графік функції наведено нижче.

CC ЗА NC-SA

Оскільки ми знаємо, що межа x ² та cos (x) існує, ми можемо знайти межу цієї функції, застосувавши Правило продукту або пряму заміну:

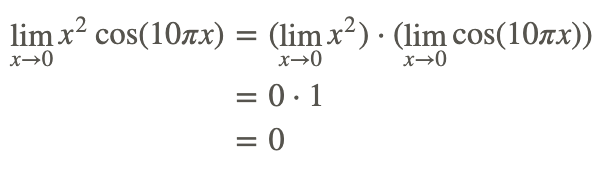
Отже,

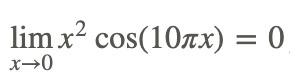
Також з графіка функції відзначимо, що функція обмежена графами x2 та −x2, які обидва дорівнюють 0 при x=0. Має сенс, що межа вихідної функції має дорівнювати 0.

Теорема про стискання

Ця особливість, що межа функції може бути наслідком того, що функція обмежена або стискається двома іншими функціями, є основою для теореми Стиснення. Теорема стискання (також відома як теорема сендвіча) стверджує:

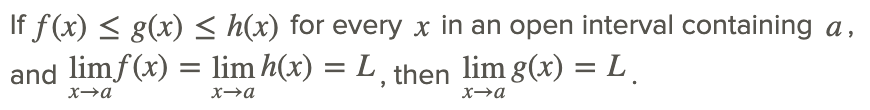
Іншими словами, якщо ми можемо знайти межі для функції, які мають однакову межу, то межа функції, яку вони пов'язані, повинна мати однакову межу. Зауважте, що a і L можуть бути будь-якою константою або навіть ∞ або −∞.

Однією з важливих тригонометричних меж, яку можна частково довести за допомогою теореми стискання, є:

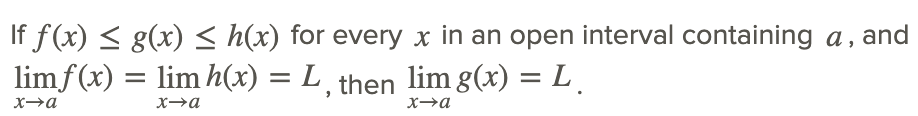
Іншими словами, якщо ми можемо знайти межі для функції, які мають однакову межу, то межа функції, яку вони пов'язані, повинна мати однакову межу. Зауважте, що a і L можуть бути будь-якою константою або навіть ∞ або −∞.

Однією з важливих тригонометричних меж, яку можна частково довести за допомогою теореми стискання, є:

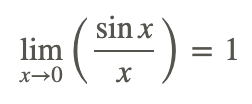
де x - в радіановій мірі.

Ще одним важливим тригонометричним межею є

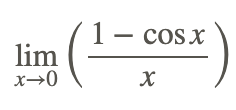
Пряма заміна не може бути використана для оцінки межі, оскільки вона дає невизначену форму ⁰/₀. Замість цього перетворіть проблему в іншу форму і вирішуйте.

---

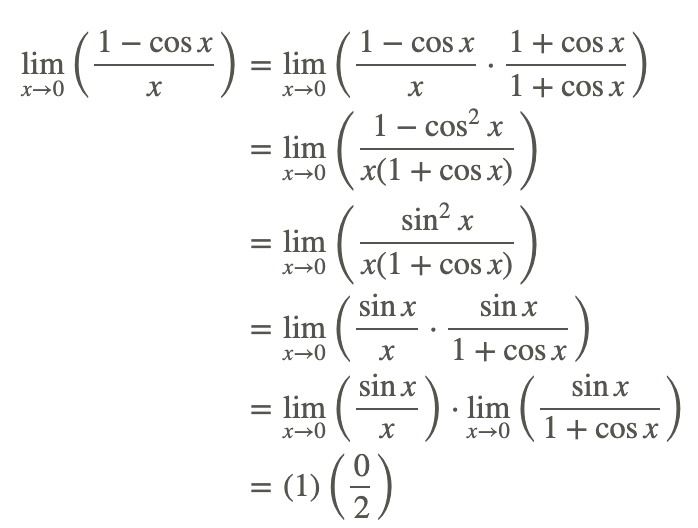
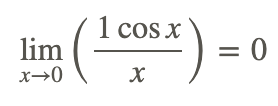
Приклади

Приклад 1

Раніше вас запитали, чи ускладнюють періодичний характер тригонометричних функцій та обмежений або нескінченний діапазон окремих тригонометричних функцій оцінювання меж за участю тригонометричних функцій.

Як ви можете собі уявити і бачили в цій концепції, деякі межі, що стосуються тригонометричних функцій, можна легко оцінити шляхом прямої підміни, а деякі розвивають багато роботи, щоб змінити форму з невизначеної або невизначеної форми. Визначення кінцевої поведінки виразу, що включає тригонометричну функцію, також може бути складним і вимагати застосування таких принципів, як теорема стискання для отримання результату. Немає легкої відповіді!

Приклад 2

Знайти

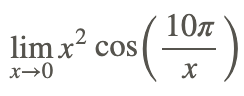
Пряма заміна не може бути використана для оцінки межі, оскільки ^10π/_x не визначено, коли x = 0.

Однак теорему про стискання можна використовувати наступним чином:

1. Ми знаємо, що косинус залишається між -1 і 1, тому

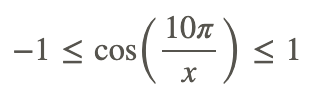
для будь-якого x в області функції (тобто будь-якого x0).

2. Оскільки x ² завжди невід'ємний, ми можемо помножити вищевказану нерівність на x ²:

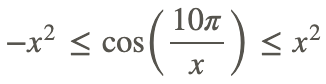
3. Початкова функція обмежена x ² та −x ² та

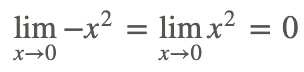
4. Тому за теоремою стискання:

---

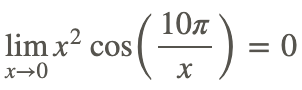
Рецензія

---

Огляд (Відповіді)

Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 2.7.

---

Лексика

Термін	Визначення
невизначені	У математиці вираз є невизначеною, якщо вона точно не визначена. Існує сім невизначених форм: 00,0⋅∞, ∞, ∞, ∞, ∞, θ 0 та 1^\ infty.
межа	Межа - це значення, до якого наближається вихід функції, коли вхід функції наближається до заданого значення.
теорема стискання	Теорема стискання (також відома як теорема сендвіча) використовується для пошуку межі функції шляхом обмеження її між двома іншими функціями, кожна з яких має однакову межу.

---

Додаткові ресурси

PLIX: Грайте, вчіться, взаємодійте, досліджуйте - оцінюйте межі засмаги (x)

Відео: Визначення меж за участю тригонометричних функцій

Практика: Основні тригонометричні межі

Реальний світ: Я полечу