8.14: Правила роздумів
- Page ID
- 54919
Визначення та державні правила, що описують роздуми за допомогою нотації
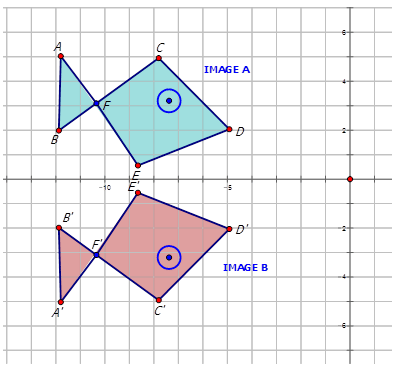
На малюнку нижче показана форма двох рибок. Напишіть правило відображення для відображення зображення\(A\) на зображення\(B\).
У геометрії трансформація - це операція, яка переміщує, перевертає або змінює фігуру для створення нової форми. Відображення є прикладом трансформації, яка приймає форму (називається попереднім зображенням) і перевертає її поперек лінії (званої лінією відображення) для створення нової форми (званої зображенням). Вивчаючи координати відбитого зображення, можна визначити лінію відображення. Найбільш поширеними лініями відображення є\(x\) -вісь,\(y\) -вісь, або лінії\(y=x\) або\(y=−x\).
Попереднє зображення вище було відображено поперек\(y\) -осі. Це означає, що всі координати x були помножені на -1. Описати відображення можна словами, або наступними позначеннями:
\(r_{y-axis} (x,y)\rightarrow (−x,y)\)
Зверніть увагу, що позначення говорить вам, як саме змінюється кожна\((x,y)\) точка в результаті перетворення.
Давайте знайдемо зображення точки\((3, 2)\), яка зазнала відображення по наступних лініях:
- \(x\)-вісь,
Відображення поперек\(x\) -осі:\(r_{x-axis} (3,2)\rightarrow (3,−2)\)
- \(y\)-вісь
Відображення поперек\(y\) -осі:\(r_{y-axis} (3,2)\rightarrow (3,−2)\)
- Лінія\(y=x\)
Відображення через лінію\(y=x\):\(r_{y=x} (3,2)\rightarrow (2,3)\)
- Лінія\(y=−x\).
Відображення через лінію\(y=−x\):\(r_{y=−x} (3,2)\rightarrow (−2,−3)\)

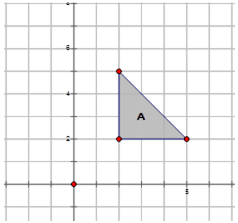
Тепер давайте відобразити зображення на діаграмі нижче\(A\) в наступних рядках і запишемо позначення для кожного відображення:
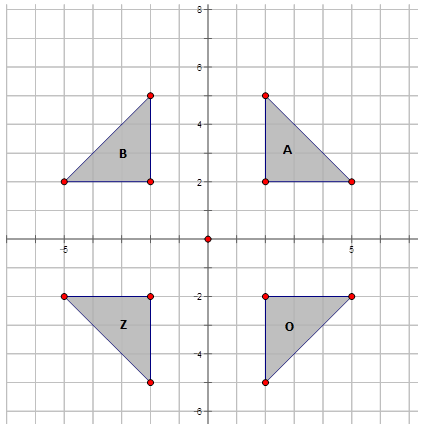
- Поперек\(y\) -осі і позначте його\(B\).
Відображення поперек\(y\) -осі:\(r_{y-axis} A\rightarrow B=r_{y-axis} (x,y)\rightarrow (−x,y)\)
- Поперек\(x\) -осі і позначте його\(O\).
Відображення поперек\(x\) -осі:\(r_{x-axis} A\rightarrow O=r_{x-axis} (x,y)\rightarrow (x,−y)\)
- Через лінію\(y=−x\) і позначте її\(Z\).
Відображення через\(y=−x\):\(r_{y=−x} A\rightarrow Z=r_{y=−x} (x,y)\rightarrow (−y,−x) \)
Нарешті, давайте напишемо позначення, яке представляє відображення попереднього зображення до зображення на діаграмі нижче:
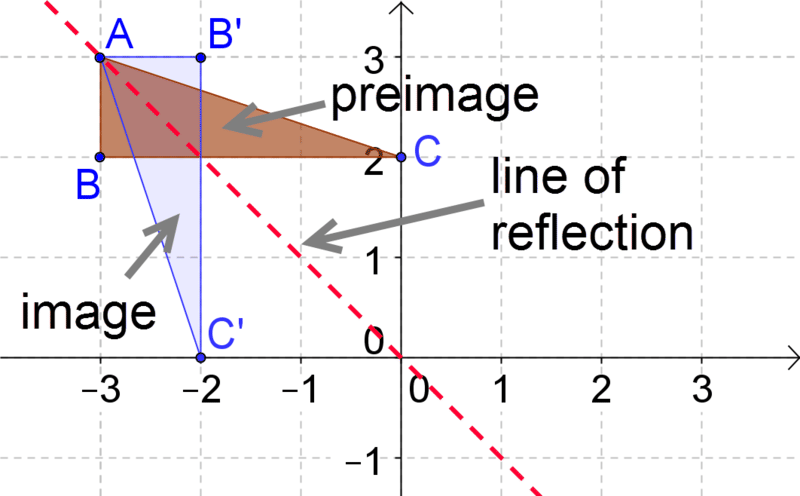
Це відображення поперек лінії\(y=−x\). Позначення є\(r_{y=−x} (x,y)\rightarrow (−y,−x)\).
Приклад\(\PageIndex{1}\)
Раніше вам давали задачу про малюнок нижче, який показує візерунок з двох риб. Запишіть правило відображення зображення A\) на Image B\).

Рішення
Щоб відповісти на це питання, подивіться координатні точки для зображень A та зображення B.
| Зображення A | \(A(−11.8,5)\) | \(B(−11.8,2)\) | \(C(−7.8,5)\) | \(D(−4.9,2)\) | \(E(−8.7,0.5)\) | \(F(−10.4,3.1)\) |
| Зображення B | \(A′(−11.8,−5)\) | \(B′(−11.8,−2)\) | \(C′(−7.8,−5)\) | \(D′(−4.9,−2)\) | \(E′(−8.7,−0.5)\) | \(F′(−10.4,−3.1)\) |
Зверніть увагу, що всі\(y-coordinates have changed sign. Therefore Image A has reflected across the \(x\) -осі. Щоб написати правило для цього роздуму, ви б написали:\(r_{x-axis} (x,y)\rightarrow (x,−y)\).
Приклад\(\PageIndex{2}\)
Томас описує відображення як точку\(J moving from \(J(−2,6)\) на\(J′(−2,−6)\). Напишіть позначення, щоб описати це відображення для Томаса.
\(J:(−2,6)\qquad J′:(−2,−6)\)
Рішення
Так як y-координата множиться на -1 і\(x-coordinate remains the same, this is a reflection in the \(x\) -вісь. Позначення це:\(r_{x-axis} J\rightarrow J′=r_{x-axis} (−2,6)\rightarrow (−2,6)\)
Приклад\(\PageIndex{3}\)
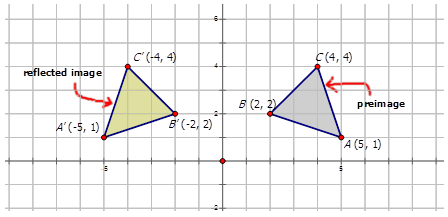
Напишіть позначення, яке представляє відображення жовтого діаманта на відображеному зеленому діаманті на діаграмі нижче.
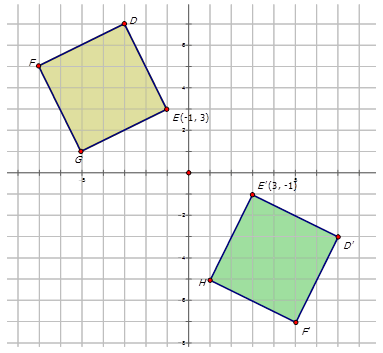
Рішення
Для того, щоб написати позначення для опису відображення, виберіть одну точку на попередньому зображенні (жовтий ромб), а потім відбиту точку на зеленому діаманті, щоб побачити, як точка рухалася. Зверніть увагу, що точка\(E\) показана на схемі:
\(E(−1,3)\rightarrow E′(3,−1)\)
Оскільки обидва\(x\) - і\(y\) -координати є зворотними числами, відображення знаходиться в рядку\(y=x\). Позначення для цього відображення було б:\(r_{y=x} (x,y)\rightarrow (y,x)\).
Приклад\(\PageIndex{4}\)
Карен грала з програмою малювання на своєму комп'ютері. Вона створила наступні діаграми, а потім хотіла визначити перетворення. Напишіть правило позначення, яке представляє перетворення фіолетової та синьої діаграми на помаранчеву та синю діаграму.
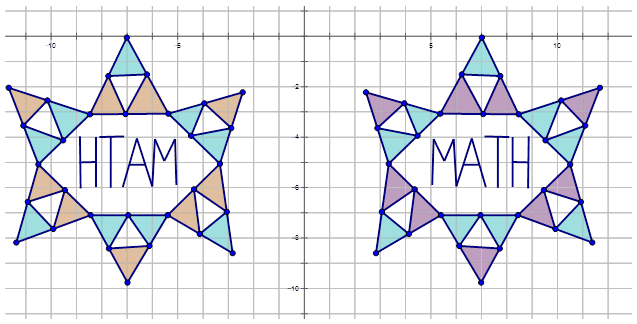
Рішення
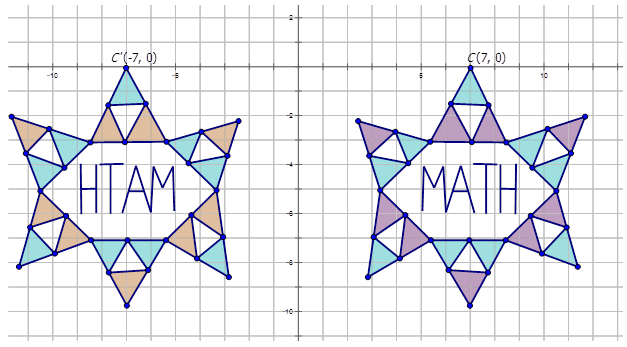
Для того, щоб написати позначення для опису перетворення, виберіть одну точку на попередньому зображенні (фіолетова та синя діаграма), а потім перетворену точку на помаранчевій та синій діаграмі, щоб побачити, як точка перемістилася. Зверніть увагу, що точка А показана на схемі:
\(C(7,0)\rightarrow C′(−7,0)\)
Оскільки обидві координати x множаться лише на -1, перетворення є відображенням у\(y\) -осі. Позначення для цього відображення було б:\(r_{y-axis} (x,y)\rightarrow (−x,y)\).
Рецензія
Напишіть позначення, щоб описати рух точок у кожному з відображень нижче.
- \(S(1,5)\rightarrow S′(−1,5)\)
- \(W(−5,−1)\rightarrow W′(5,−1)\)
- \(Q(2,−5)\rightarrow Q′(2,5)\)
- \(M(4,3)\rightarrow M′(−3,−4)\)
- \(B(−4,−2)\rightarrow B′(−2,−4)\)
- \(A(3,5)\rightarrow A′(−3,5)\)
- \(C(1,2)\rightarrow C′(2,1)\)
- \(D(2,−5)\rightarrow D′(5,−2)\)
- \(E(3,1)\rightarrow E′(−3,1)\)
- \(F(−4,2)\rightarrow F′(−4,−2)\)
- \(G(1,3)\rightarrow G′(1,−3)\)
Напишіть позначення, яке представляє відображення зображення попереднього зображення для кожної діаграми нижче.
-
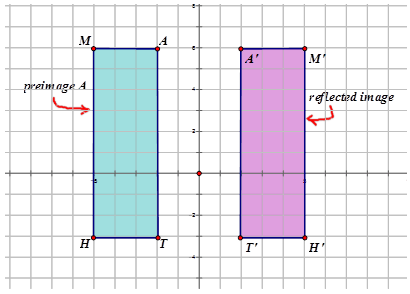
Малюнок\(\PageIndex{12}\) -
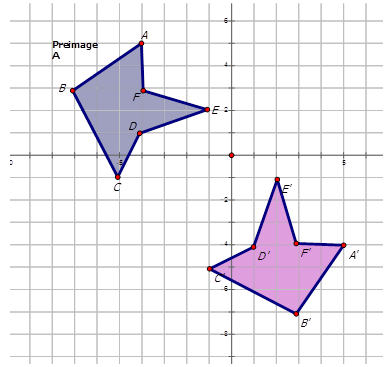
Малюнок\(\PageIndex{13}\) -
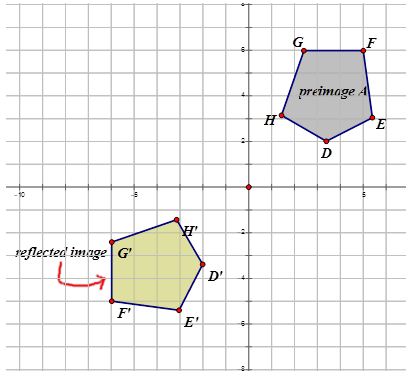
Малюнок\(\PageIndex{14}\) -
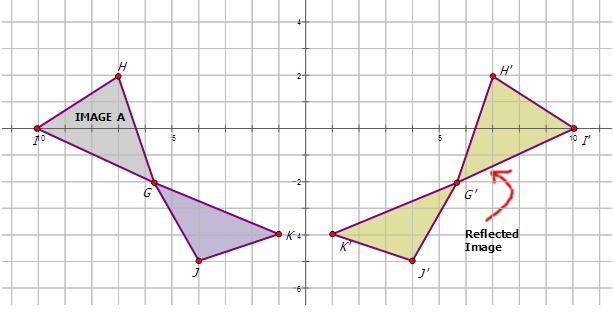
Малюнок\(\PageIndex{15}\)
Огляд (Відповіді)
Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 10.6.
Додаткові ресурси
Інтерактивний елемент
Практика: Правила роздумів