8.11: Правила ротації

Державні правила, що описують дані обертання.

Правила обертання

На малюнку нижче показана форма двох рибок. Запишіть правило відображення для повороту зображення A до зображення B.

Малюнок$\PageIndex{1}$

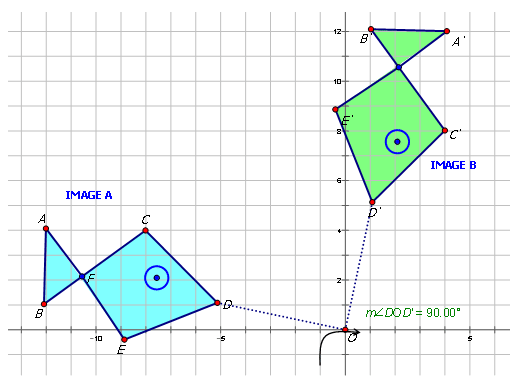
У геометрії трансформація - це операція, яка переміщує, перевертає або змінює фігуру для створення нової форми. Обертання - це приклад перетворення, коли фігура обертається навколо певної точки (званої центром обертання), певної кількості градусів. Загальні обертання щодо походження показані нижче:

Центр обертання	Кут повороту	Передзображення (точка P)	Повернене зображення (точка P′)	Позначення (точка P′)
(0, 0)	$90^{\circ}$(або$−270^{\circ}$)	$(x,y)$	$(−y,x)$	$(x,y)\rightarrow (−y,x)$
(0, 0)	$180^{\circ}$(або$−180^{\circ}$)	$(x,y)$	$(−x,−y)$	$(x,y)\rightarrow (−x,−y)$
(0, 0)	$270^{\circ}$(або$−90^{\circ}$)	$(x,y)$	$(y,−x)$	$(x,y)\rightarrow (y,−x)$

Можна описати обертання словами, або з позначеннями. Розглянемо зображення нижче:

Малюнок$\PageIndex{2}$

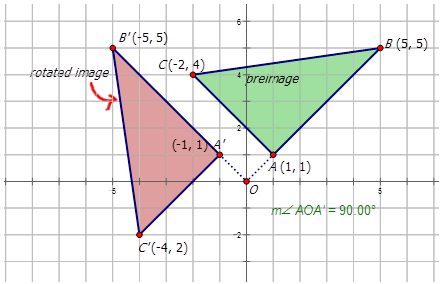
Зверніть увагу, що попереднє зображення обертається навколо вихідної$90^{\circ}$ CCW. Якби ви описували повернуте зображення за допомогою нотації, ви б написали наступне:

$R_{90^{\circ}}(x,y)=(−y,x)$

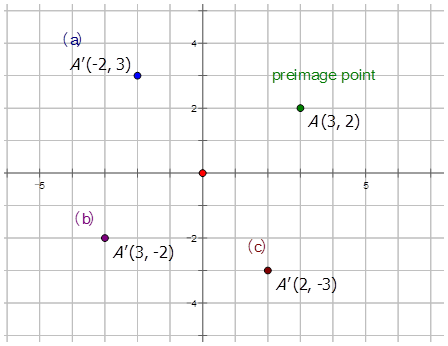
Напишемо позначення для опису наступних обертань CCW на точці (3, 2)\) і намалюємо зображення:

1. про походження в$90^{\circ}$

Обертання про походження при$90^{\circ}: \(R_{90^{\circ}}(x,y)=(−y,x)$

2. про походження в$180^{\circ}$

Обертання про походження при$180^{\circ}$:$R_{180^{\circ}}(x,y)=(−x, −y)$

3. про походження в$270^{\circ}$

Обертання щодо походження на 270^ {\ circ}:$R_270^{\circ}(x,y)=(y,−x)$

Малюнок$\PageIndex{3}$

Тепер давайте виконаємо наступні обертання на зображенні,$A$ показаному нижче на схемі нижче, і опишемо обертання:

Малюнок$\PageIndex{4}$

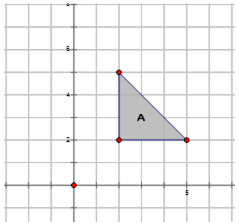
1. про походження в$90^{\circ}$, і позначити його$B$.

Обертання про походження при$90^{\circ}$:$R_{90^{\circ}}A\rightarrow B=R_{90^{\circ}}(x,y)\rightarrow (−y,x)$

2. про походження в$180^{\circ}$, і позначити його$O$.

Обертання про походження при$180^{\circ}$:$R_{180^{\circ}}A\rightarrow O=R_{180^{\circ}}(x,y)\rightarrow (−x,−y)$

3. про походження в$270^{\circ}$, і позначити його$Z$.

Обертання про походження при$270^{\circ}$:$R_{270^{\circ}}A\rightarrow Z=R270^{\circ}(x,y)\rightarrow (y,−x)$

Малюнок$\PageIndex{5}$

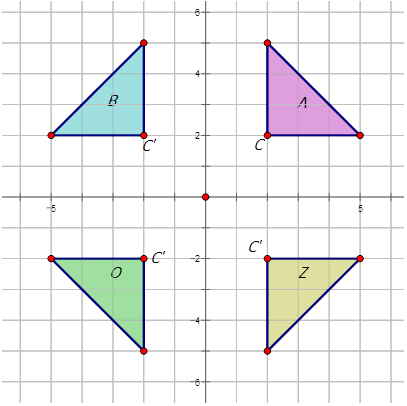
Нарешті, давайте напишемо позначення, яке представляє обертання попереднього зображення A до повернутого зображення J на діаграмі нижче:

Малюнок$\PageIndex{6}$

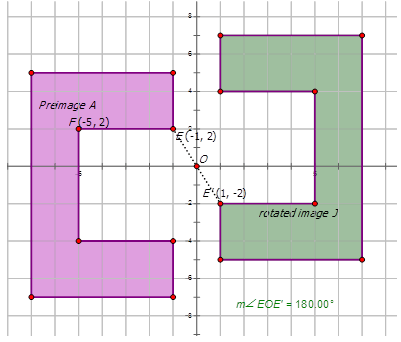
Спочатку виберіть точку на діаграмі, щоб побачити, як вона обертається.

$E:(−1,2)\qquad E′:(1,−2)$

Зверніть увагу, як обидва$x$ - і$y$ -координати множаться на -1. Це вказує на те, що попереднє зображення$A$ відбивається про походження за допомогою$180^{\circ}$ CCW для формування повернутого зображення J. Тому позначення є$R_{180^{\circ}}A\rightarrow J=R_{180^{\circ}}(x,y)\rightarrow (−x,−y)$.

Приклад$\PageIndex{1}$

Раніше вам давали малюнок нижче, на якому зображений візерунок з двох рибок. Напишіть правило відображення для повороту Image$A$ to Image$B$.

Малюнок$\PageIndex{7}$

Рішення

Зверніть увагу, що вимірювання кута є,$90^{\circ}$ а напрямок - за годинниковою стрілкою. Тому зображення$A$ було повернуто$−90^{\circ}$ у форму зображення$B$. Щоб написати правило для цієї ротації, ви б написали:$R_{270^{\circ}}(x,y)=(−y,x)$.

Приклад$\PageIndex{}$

Томас описує обертання як точку,$J$ що рухається від$J(−2,6)$ до$J′(6,2)$. Напишіть позначення, щоб описати це обертання для Томаса.

$J:(−2,6)\qquad J′:(6,2)$

Малюнок$\PageIndex{8}$

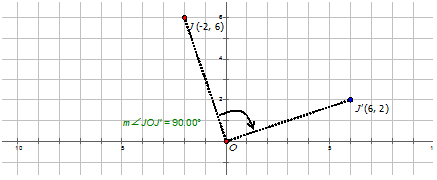
Рішення

Оскільки$x$ -координата множиться на -1,$y$ координата -залишається незмінною, і, нарешті,$x$ - і$y$ -координати змінюються місцями, це обертання про початок на$270^{\circ}$ або$−90^{\circ}$. Позначення це:$R_{270^{\circ}}J\rightarrow J′=R_270^{\circ}(x,y)\rightarrow (y,−x)$

Приклад$\PageIndex{1}$

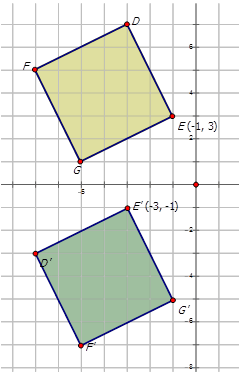
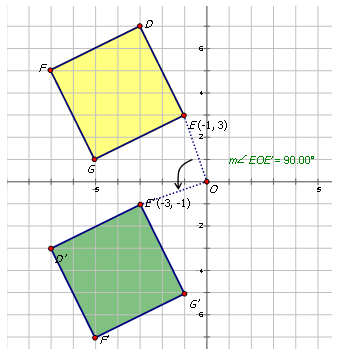
Напишіть позначення, яке представляє обертання жовтого діаманта до повернутого зеленого діаманта на діаграмі нижче.

Малюнок$\PageIndex{9}$

Рішення

Для того, щоб написати позначення для опису обертання, виберіть одну точку на попередньому зображенні (жовтий ромб), а потім повернену точку на зеленому діаманті, щоб побачити, як точка перемістилася. Зверніть увагу, що точка E\) показана на схемі:

$E(−1,3)\rightarrow E′(−3,−1)$

Оскільки обидва$x$ - і$y$ -координати є зворотними місцями, а$y$ координата -помножена на -1, обертання становить приблизно початок$90^{\circ}$. Позначення для цього обертання було б:$R_{90^{\circ}}(x,y)\rightarrow (−y,x)$.

Малюнок$\PageIndex{10}$

Приклад$\PageIndex{1}$

Карен грала з програмою малювання на своєму комп'ютері. Вона створила наступні діаграми, а потім хотіла визначити перетворення. Напишіть правило позначення, яке представляє перетворення фіолетової та синьої діаграми на помаранчеву та синю діаграму.

Малюнок$\PageIndex{11}$

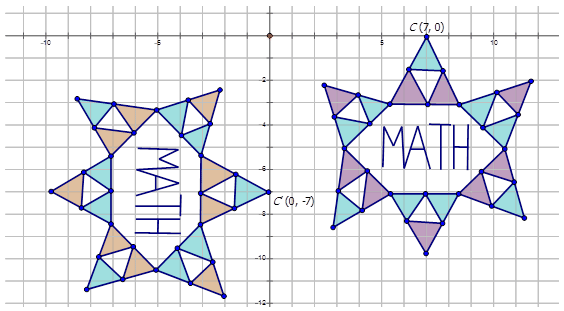
Рішення

Для того, щоб написати позначення для опису перетворення, виберіть одну точку на попередньому зображенні (фіолетова та синя діаграма), а потім перетворену точку на помаранчевій та синій діаграмі, щоб побачити, як точка перемістилася. Зверніть увагу, що точка$C$ показана на схемі:

$C(7,0)\rightarrow C′(0,−7)$

Оскільки$x$ -координати множаться лише на -1, а потім$x$ - і$y$ -координати міняються місцями, перетворення є обертанням приблизно на початок$270^{\circ}$. Позначення для цього обертання було б:$R_{270^{\circ}}(x,y)\rightarrow (y,−x)$.

Рецензія

Заповніть наступну таблицю:

Початкова точка	$90^{\circ}$Обертання	$180^{\circ}$Обертання	$270^{\circ}$Обертання	$360^{\circ}$Обертання
1. $(1, 4)$	\ (90^ {\ circ}\) Обертання» клас = "lt-k12-6036">	\ (180^ {\ circ}\) Обертання» клас = "lt-k12-6036">	\ (270^ {\ circ}\) Обертання» клас ="lt-k12-6036">	\ (360^ {\ circ}\) Обертання» клас = "lt-k12-6036">
2. $(4, 2)$	\ (90^ {\ circ}\) Обертання» клас = "lt-k12-6036">	\ (180^ {\ circ}\) Обертання» клас = "lt-k12-6036">	\ (270^ {\ circ}\) Обертання» клас ="lt-k12-6036">	\ (360^ {\ circ}\) Обертання» клас = "lt-k12-6036">
3. $(2, 0)$	\ (90^ {\ circ}\) Обертання» клас = "lt-k12-6036">	\ (180^ {\ circ}\) Обертання» клас = "lt-k12-6036">	\ (270^ {\ circ}\) Обертання» клас ="lt-k12-6036">	\ (360^ {\ circ}\) Обертання» клас = "lt-k12-6036">
4. $(-1, 2)$	\ (90^ {\ circ}\) Обертання» клас = "lt-k12-6036">	\ (180^ {\ circ}\) Обертання» клас = "lt-k12-6036">	\ (270^ {\ circ}\) Обертання» клас ="lt-k12-6036">	\ (360^ {\ circ}\) Обертання» клас = "lt-k12-6036">
5. $(-2, -3)$	\ (90^ {\ circ}\) Обертання» клас = "lt-k12-6036">	\ (180^ {\ circ}\) Обертання» клас = "lt-k12-6036">	\ (270^ {\ circ}\) Обертання» клас ="lt-k12-6036">	\ (360^ {\ circ}\) Обертання» клас = "lt-k12-6036">

Запишіть позначення, що представляє обертання попереднього зображення, до зображення для кожної діаграми нижче.

6. 

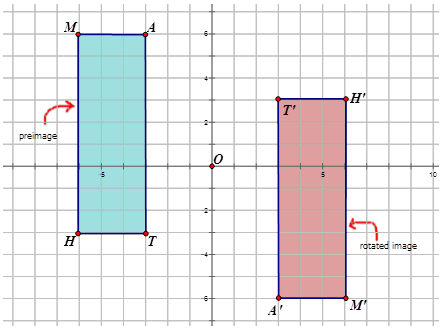
   Малюнок$\PageIndex{12}$

7. 

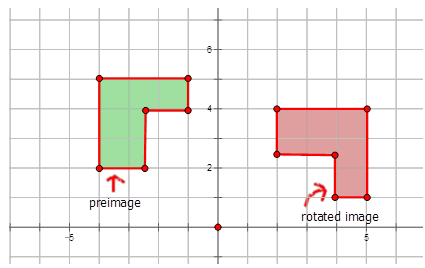
   Малюнок$\PageIndex{13}$

8. 

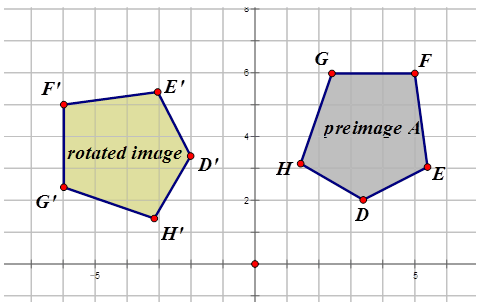
   Малюнок$\PageIndex{14}$

9. 

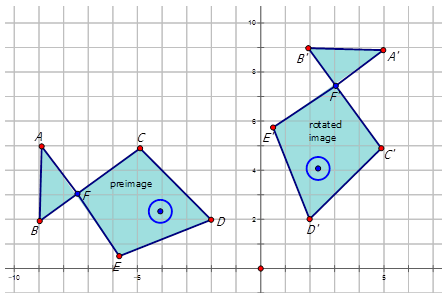
   Малюнок$\PageIndex{15}$

10. 

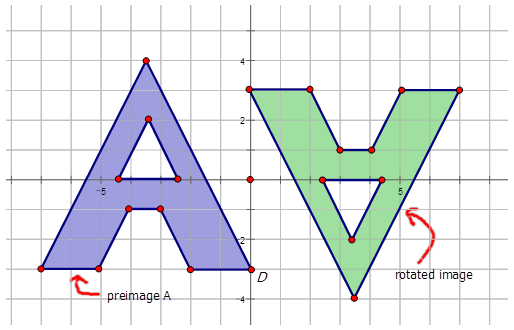
    Малюнок$\PageIndex{16}$

Запишіть позначення, що представляє обертання попереднього зображення, до зображення для кожної діаграми нижче.

11. 

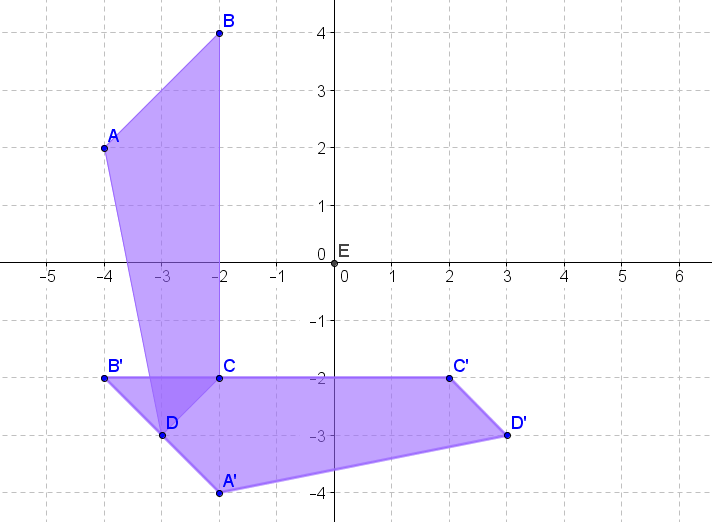
    Малюнок$\PageIndex{17}$

12. 

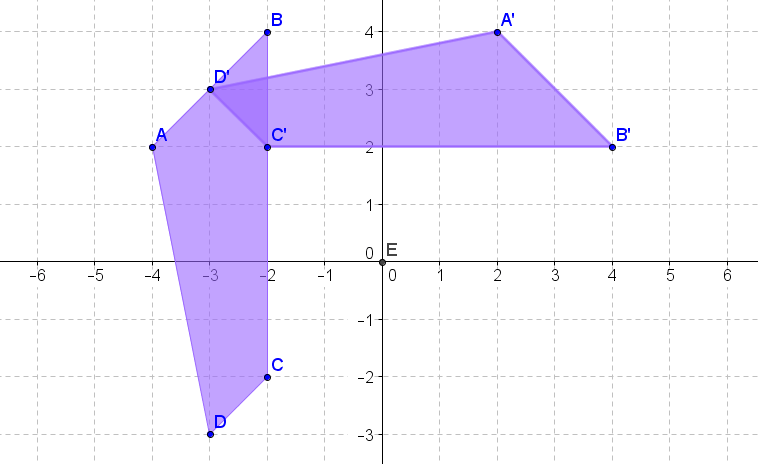
    Малюнок$\PageIndex{18}$

13. 

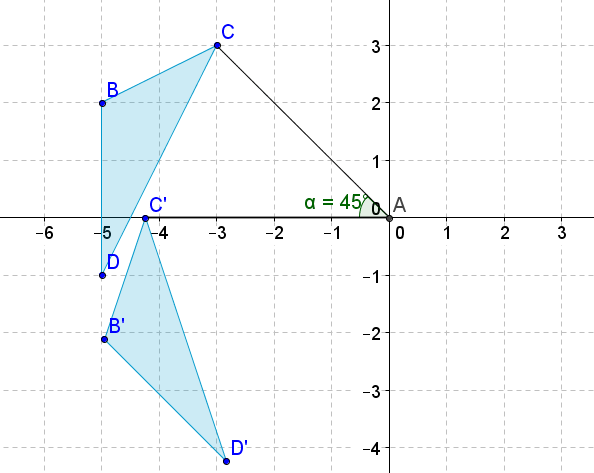
    Малюнок$\PageIndex{19}$

14. 

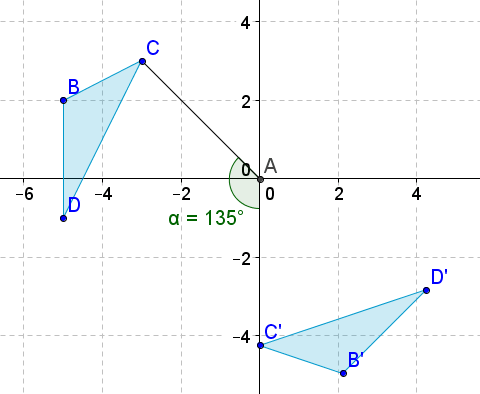
    Малюнок$\PageIndex{20}$

15. 

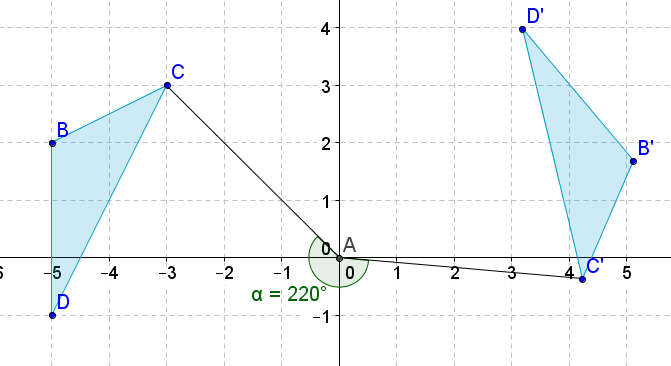
    Малюнок$\PageIndex{21}$

Огляд (Відповіді)

Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 10.9.

Додаткові ресурси

Відео: Правила обертання

Практика: Правила ротації