8.1: Визначте типи трансформації

Last updated
Save as PDF

Page ID: 54921

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Визначте перетворення, переклади, роздуми та обертання.

Трансформації в площині

Трансформація - це процес, який змінює форму, розмір або положення фігури для створення нового образу. Це функція, яка приймає точки на площині як входи і дає інші точки як виходи. Ви можете думати про трансформацію, як правило, яка підкаже вам, як створювати нові точки.

Припустимо, у вас є трансформація\(F\), яка застосовує горизонтальний коефіцієнт розтягування два до кожної точки. Нижче це перетворення застосовується до трикутника для\(S\) створення трикутника\(S'\).

\(S'\)вважається образ\(S\) по\(F\).
Також правильно сказати, що\(F\) карти\(S\) до\(S'\).
Кожна з точок на зображенні позначена символом ′, який читається як «простий».

Це допомагає показати, як точки на\(S\) відповідають пунктам на\(S'\). Наприклад, можна сказати, що «точки А карти на точку A-prime».

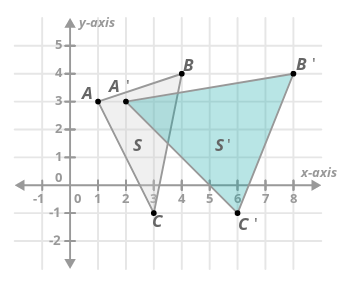
Деякі перетворення зберігають довжину і кути. Збереження довжини означає, що якщо відрізок лінії дорівнює 3 одиницям, його зображення також буде 3 одиниці. Аналогічно, збереження кутів означає, що якщо кут є\(60^{\circ}\), його зображення також буде\(60^{\circ}\).

Трансформація, яка зберігає довжину і кути, називається жорстким перетворенням.

Розпізнавання жорстких перетворень

Чи є горизонтальна розтяжка прикладом жорсткої трансформації?

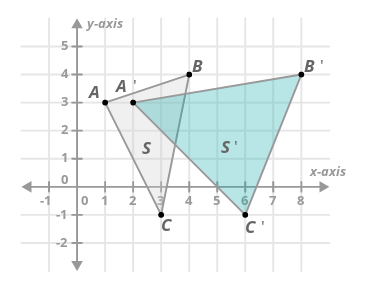
Ні. Ви можете довести це за допомогою малюнка вище, показавши, що довжина не збереглася.

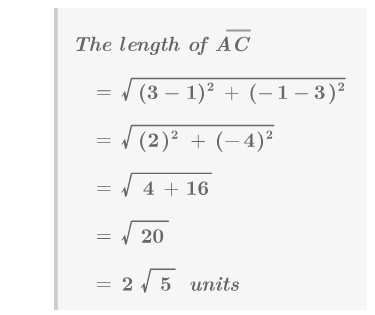
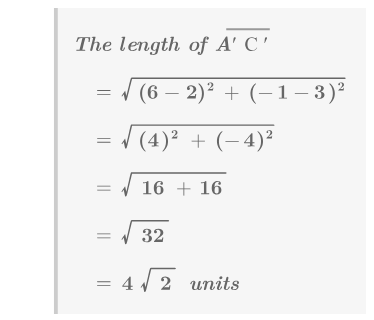
Трансформація відображає точки у формі\(K\)\(\overleftrightarrow{AB}\) поперек, щоб створити фігуру\(K′\). Чи є це відображення жорстким перетворенням?

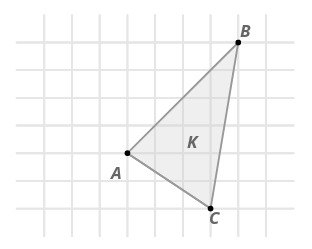
Так, роздуми - це жорсткі перетворення. Ви можете переконатися, що відстані між точками збереглися.

Трансформація перетворює точки у формі\(K\) уздовж вектора\(\rightarrow{v}\) для створення фігури\(K′\). Чи є цей переклад жорстким перетворенням?

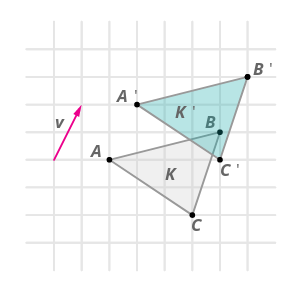
Так, переклади - це жорсткі перетворення. Ви можете переконатися, що відстані між точками збереглися.

Інтерактивний елемент

Додайте тут інтерактивний текст елемента. Це поле НЕ буде друкувати в PDF-файлах

Приклад\(\PageIndex{1}\)

Ви просуваєте книгу по столу. Насипаєте соду з банки у велику склянку. Опишіть ці дії як перетворення.

Рішення

Ковзання книги по столу - це жорстка трансформація, оскільки книга - це жорсткий предмет, який не змінює форму. Відстані та кути, що складають книгу, не змінюються, коли книга знаходиться в новому місці. Наливання соди, з іншого боку, не є жорстким перетворенням. Рідина не є жорстким предметом, і вона може змінювати форму залежно від оточення. Загальна форма соди в банці буде відрізнятися від загальної форми соди в склянці.

Приклад\(\PageIndex{2}\)

Трансформація обертає точки фігури\(K\) навколо точки,\(D\) щоб створити фігуру\(K′\). Чи виглядає це обертання жорстким перетворенням? Використовуйте алгебру, щоб довести свою відповідь.

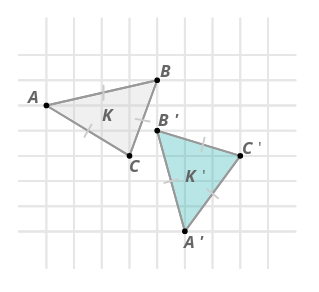
Рішення

Це, здається, жорстка трансформація.

За допомогою теореми Піфагора можна показати, що відповідні сторони мають однакову довжину. Наприклад:

\(\begin{aligned} \text{ The length of } \overline{AC} \\&=\sqrt{3^2+2^2} \\ &=\sqrt{9+4} \\ &=\sqrt{13}\text{ units } \\ \text{ The length of }\overline{A′C′} \\ &=\sqrt{3^2+2^2} \\ &=\sqrt{9+4} \\ &=\sqrt{13}\text{ units } \end{aligned}\)

Таким чином, це дійсно жорстка трансформація.

Приклад\(\PageIndex{3}\)

Що робить трансформацію жорсткою трансформацією?

Рішення

Жорсткі перетворення зберігають відстань і кути. Всі відповідні сторони будуть однакової довжини і всі відповідні кути будуть однаковою мірою.

Рецензія

Для 1-7 визначте кожне твердження як істинне чи хибне і обґрунтуйте свою відповідь.

1. Переклади - це жорсткі перетворення.

2. Обертання - це жорсткі перетворення.

3. Горизонтальні розтяжки - це жорсткі перетворення.

4. Жорсткі перетворення зберігають розташування в площині.

5. Відповідні сторони в жорстких перетвореннях мають однакову довжину.

6. Якщо це не жорстка трансформація, це не справжня трансформація.

7. Роздуми - це жорсткі перетворення.

Використовуйте наступне зображення для 8-9.

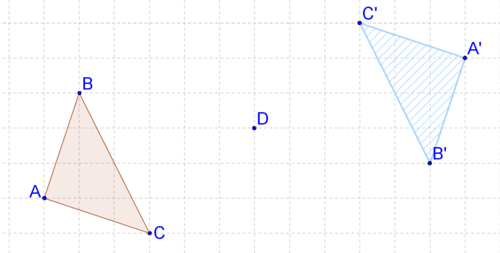
8. Опишіть перетворення своїми словами. Це схоже на жорстке перетворення?

9. Доведіть свою відповідь на #8, порівнявши довжини двох сторін.

Використовуйте наступне зображення для 10-11.

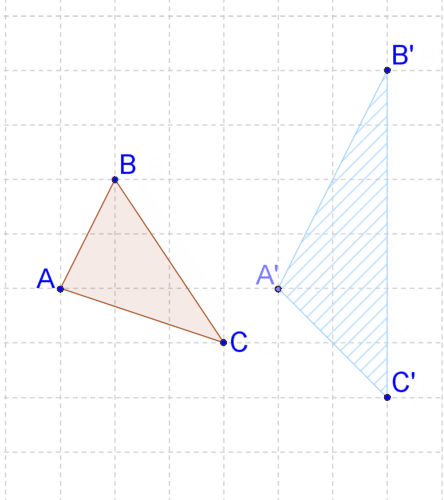
10. Опишіть перетворення своїми словами. Це схоже на жорстке перетворення?

11. Доведіть свою відповідь на #10, порівнявши довжини двох сторін.

Використовуйте наступне зображення для 12-13.

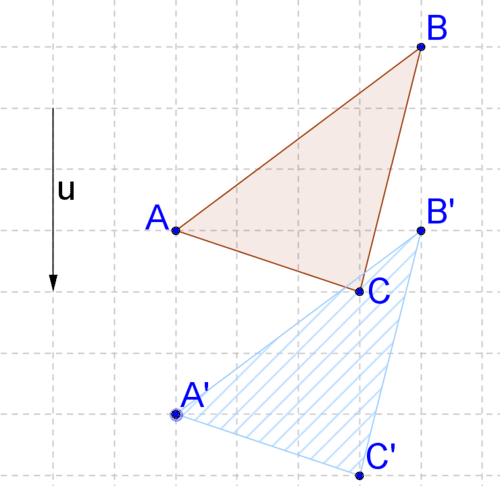
12. Опишіть перетворення своїми словами. Це схоже на жорстке перетворення?

13. Доведіть свою відповідь на #12, порівнявши довжини двох сторін.

Використовуйте наступне зображення для 14-15.

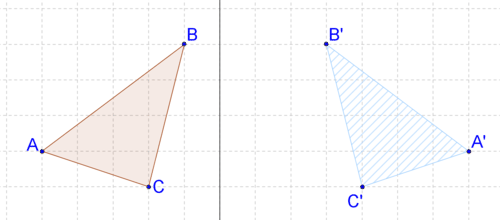
14. Опишіть перетворення своїми словами. Це схоже на жорстке перетворення?

15. Доведіть свою відповідь на #14, порівнявши довжини двох сторін.

16. Трансформація може розглядатися як рух об'єкта в площині таким чином, що кутові заходи та довжини сегментів зберігаються. Уявіть собі трикутник, який ви вирізали, лежачи рівно на аркуші плакатного паперу. Як можна перемістити трикутник так, щоб міри кутів і довжини відрізків збереглися? Як можна класифікувати та визначити різні типи рухів? Проявіть творчість. Малюйте, пишіть та обговорюйте, як більш конкретно описати та визначити типи та методи перетворень жорсткого руху.

17. Існує один тип жорсткого перетворення руху, який, здається, вимагає, щоб трикутник, описаний вище, був піднятий з плакатної дошки і перевернутий. (Математично це не те, що відбувається, але це виглядає так з нашої тривимірної точки зору.) Як можна визначити і описати цю трансформацію?

18. Іноді ми можемо описати перетворення в координатній площині. Наприклад, можна спеціально змінювати координати вершин багатокутника відповідно до правила. Подумайте, як ви можете змінити координати точки та якими наслідками буде кожен тип модифікації. Експеримент. Намалюйте багатокутник на координатній площині та змініть координати відповідно до різних правил, а потім намалюйте отримані зображення. Напишіть і обговоріть свої висновки.

19. Визначте та опишіть перетворення,\(A\) які\(A'\)\(A''\) відображаються\(A'''\) нижче.

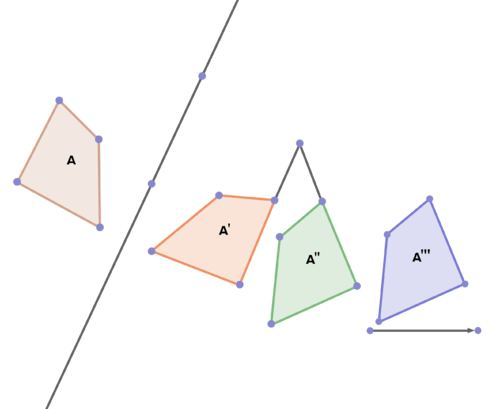
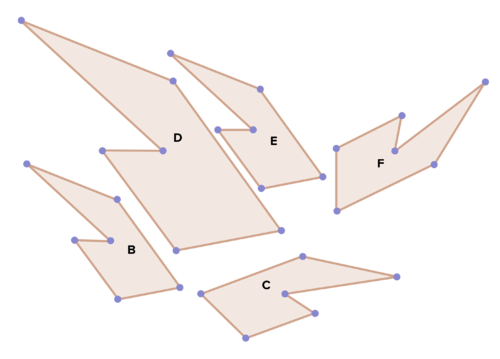
20. Деякі з наведених нижче зображень представляють жорсткі перетворення руху багатокутника B, а деякі - ні. Вирішіть, що робити, а які ні, і поясніть свій вибір. Визначте та опишіть ті, які роблять.

Огляд (Відповіді)

Щоб переглянути відповіді на огляд, натисніть тут.

Додаткові ресурси

Інтерактивний елемент

Практика: Визначте типи трансформації