Skip to main content
LibreTexts - Ukrayinska

6.3: Використовуйте діаметр, радіус і Pi

  1. Last updated
  2. Save as PDF
  • Page ID
    54476

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Визначте постійне співвідношення\(\pi= \dfrac{C}{d}\).

    Пі

    F-D_FCDDBE80259AF02F63aa7C39FF6A7 Дие6CFF9F5E69B7582B11+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_jpg
    Малюнок\(\PageIndex{1}\)

    Карлі доводиться сходити в магазин і дістати скатертину для круглого столу в їдальні. Для того щоб отримати скатертину потрібного розміру, їй потрібно знати відстань від однієї сторони столу до іншої сторони. Трифутовий мірник, який вона має, може вимірювати лише до центру столу або на півдорозі поперек. Як Карла може з'ясувати відстань через круглий стіл лише за допомогою міри, а потім використати цю інформацію, щоб дізнатися окружність таблиці?

    У цій концепції ви дізнаєтеся взаємозв'язок між діаметром і радіусом і визначите пі як відношення діаметра до окружності в колі.

    Коло Відносини

    Для роботи з колами потрібно знати різні частини кола і як вимірюються ці ключові частини.

    Можна виміряти відстань по центру кола. Ця відстань називається діаметром кола.

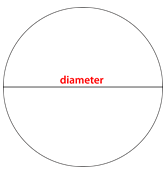
    F-D_35E629FC17A398E3E001892195d395559CA65cbec97422FA0D4E2A0+зображення_thumb_поштова листівка_крихітка_зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{2}\)

    Можна виміряти відстань від центру кола до зовнішнього краю. Ця відстань називається радіусом.

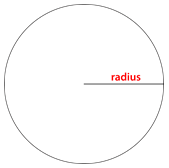
    F-D_2AE05E75C94B2A1cd1d3FFD7DA4056b269f17d7c06301C987d14bf+зображення_thumb_поштова листівка_крихітка_зображення_thumb_поштова листівка_крихітка_
    Малюнок\(\PageIndex{3}\)

    Зверніть увагу, що радіус дорівнює половині міри діаметра.

    Ви також можете виміряти периметр кола. Ця відстань називається окружністю кола.

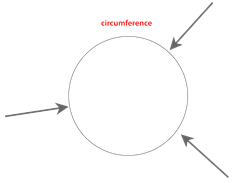
    F-D_9a02fd979b2d5787cb25f7174269b87a21f6c6a3856e612FE27292b+зображення_тумбі_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{4}\)

    Архімеду, математику в Стародавній Греції, приписують з'ясування взаємозв'язку між діаметром і окружністю кола. Архімед виявив, що якщо взяти відстань по колу (діаметру) і розтягнути його по колу, потрібно буде трохи більше 3 відрізків діаметра, щоб пройти по колу кола.

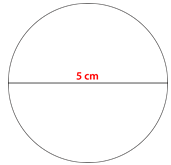
    F-D_00A9820F5E29A74BF0D6AAB7720FE3AE26AE0902568A2BE9B296E+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{5}\)

    Припустимо, діаметр цього кола дорівнює 5 см, в такому випадку окружність кола в три і трохи більше разів перевищує 5 см, або трохи менше 16 см.

    Ставлення діаметра до окружності називається пі,\(\pi\). Числове значення pi є незавершеним десятковим, що означає, що його не можна записати точно як числівник, оскільки десяткові розряди ніколи не закінчуються і не утворюють шаблон. Так, число 3.14 використовується для представлення пі і використовується для оцінки окружності кола.

    Приклад\(\PageIndex{1}\)

    Раніше вам давали проблему про Карлу і її клопоту виміряти діаметр круглого столу.

    Карла все ще обговорювала, як знайти діаметр круглого столу, коли її мати ходила в їдальню. Коли Карла пояснила проблему своїй мамі, її мама сказала їй, якщо трифутовий мірник вимірює відстань від краю столу до центральної точки, то це був радіус столу. Знаючи, що радіус таблиці становив 3 фути, Карла знала, що вона може використовувати формулу співвідношення радіуса і діаметра, щоб з'ясувати відстань від однієї сторони таблиці до іншої.

    Рішення

    Спочатку Карла підставила дане вимірювання в формулу діаметра і радіуса.

    \(\begin{aligned} 2 (\text{ radius })=\text{ diameter } \\ 2 (3\text{ feet })=\text{ diameter }\end{aligned}\)

    Далі вона множимо 2 рази 3.

    \(6\text{ feet }= \text{ diameter }\)

    Діаметр столу становить 6 футів.

    Карла могла б використати цю інформацію, щоб з'ясувати окружності таблиці шляхом множення діаметра та пі (3,14).

    Приклад\(\PageIndex{2}\)

    Використовуйте задане значення для радіуса, щоб знайти діаметр.

    Якщо радіус кола дорівнює 3, який діаметр?

    Рішення

    Для початку зверніть увагу на визначення радіуса і діаметра. Радіус дорівнює половині діаметра або діаметр в два рази більше довжини радіуса.

    \(2 (\text{ radius })=\text{ diameter }\)

    Далі множимо радіус на 2, щоб отримати 6.

    \(2(3)=6\)

    Відповідь - 6.

    Приклад\(\PageIndex{3}\)

    Якщо коло має діаметр 14 дюймів, який його радіус?

    Рішення

    Спочатку підставляємо дане вимірювання в формулу діаметра і радіуса.

    \(\begin{aligned} 2 (\text{ radius })&=\text{ diameter }\\ 2r&=14 \text{ inches }\end{aligned}\)

    Далі розділіть обидві сторони на 2.

    \(\begin{aligned}\dfrac{2r}{2}&=\dfrac{14}{2} \\ r&=7 \end{aligned}\)

    Відповідь - 7.

    Приклад\(\PageIndex{4}\)

    Якщо коло має радіус 11 дюймів, який її діаметр?

    Рішення

    Спочатку підставляємо дане вимірювання в формулу діаметра і радіуса.

    \(\begin{aligned}2(\text{ radius })=\text{ diameter } \\ 2(11\text{ inches })=\text{ diameter } \end{aligned}\)

    Далі множимо 2 і 11.

    \(22=\text{ diameter }\)

    Відповідь - 22.

    Приклад\(\PageIndex{5}\)

    Якщо коло має діаметр 18 дюймів, який його радіус?

    Рішення

    Спочатку підставляємо відомі значення в рівняння.

    \(2(r)=18\)

    Далі виконайте математику і розділіть обидві сторони на 2.

    \(\begin{aligned}\dfrac{2r}{2}&=\dfrac{18}{2} \\ r&=9\end{aligned}\)

    Відповідь - 9.

    Рецензія

    З огляду на кожен радіус, визначте діаметр.

    1. \(r=4\text{ in. }\)
    2. \(r=6\text{ in. }\)
    3. \(r=5\text{ in. }\)
    4. \(r=12\text{ in. }\)
    5. \(r=16\text{ ft. }\)
    6. \(r=28\text{ mm. }\)
    7. \(r=12.5\text{ ft. }\)
    8. \(r=1.25\text{ m. }\)

    З огляду на кожен діаметр, визначте радіус.

    1. \(d=12\text{ m. }\)
    2. \(d=18\text{ m. }\)
    3. \(d=12.5\text{ in. }\)
    4. \(d=18.5\text{ ft. }\)
    5. \(d=9.8\text{ in. }\)
    6. \(d=1.45\text{ mm. }\)
    7. \(d=1.75\text{ ft. }\)
    8. \(d=2.5\text{ ft. }\)
    9. \(d=221.25\text{ m. }\)

    Лексика

    Термін Визначення
    \ пі \(\pi\)(Pi) - відношення окружності кола до його діаметру. Це ірраціональне число, яке приблизно дорівнює 3,14.
    Архімед Архімед був грецьким математиком і філософом. Серед багатьох інших речей він визначив 3,14 як пі.
    Окружність Окружність кола - це міра відстані навколо зовнішнього краю кола.
    Діаметр Діаметр - це міра відстані через центр кола. Діаметр дорівнює подвоєної мірі радіуса.
    Пі \(\pi\)(Pi) - відношення окружності кола до його діаметру. Це ірраціональне число, яке приблизно дорівнює 3,14.
    Радіус Радіус кола - це відстань від центру кола до краю кола.

    Інтерактивний елемент

    Відео: Кола: радіус, діаметр і окружність

    Практика: Використовуйте діаметр, радіус і Pi