Skip to main content
LibreTexts - Ukrayinska

6.2: Визначте компоненти кола

  1. Last updated
  2. Save as PDF
  • Page ID
    54492

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Компоненти, окружність і площа кіл.

    Частини кіл

    Кола

    Коло - це сукупність всіх точок на площині, які знаходяться на однаковій відстані від певної точки, званої центром. Центр кола внизу - точка А. Ми називаємо це коло «коло А», і воно позначається\(\bigodot A\).

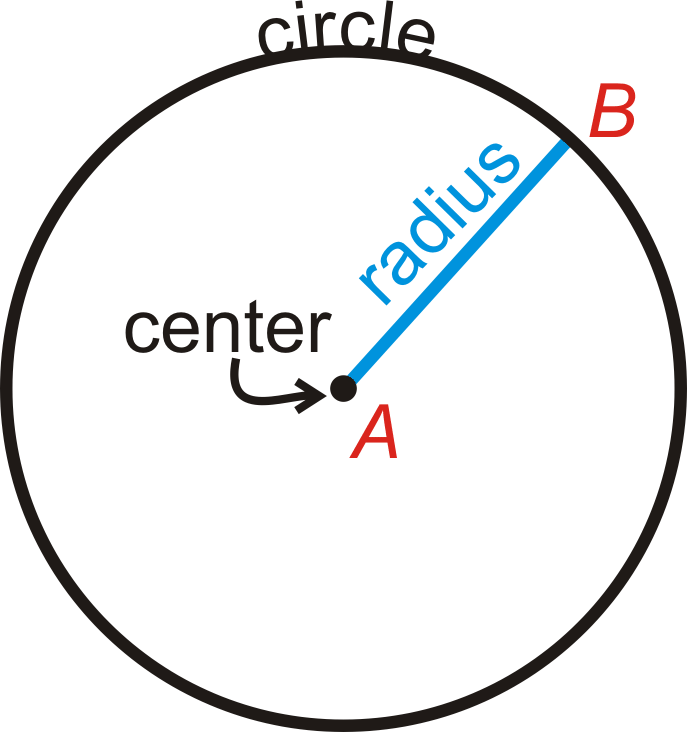
    Ф-Д_234Е9 КС5Ф3ААА0СА982Д5ФБ5ДБ5ДБ075217С3БК 5093884 БК 6КК41ФА+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Важливі деталі кола

    Радіус: Відстань від центру кола до його зовнішнього обідка.

    Акорд: відрізок лінії, кінцеві точки якого знаходяться на колі.

    Діаметр: хорда, яка проходить через центр кола. Довжина діаметра в два рази перевищує довжину радіуса.

    Січна: лінія, яка перетинає коло у двох точках.

    Дотична: лінія, яка перетинає коло рівно в одній точці.

    Точка дотику: точка, де дотична лінія торкається кола.

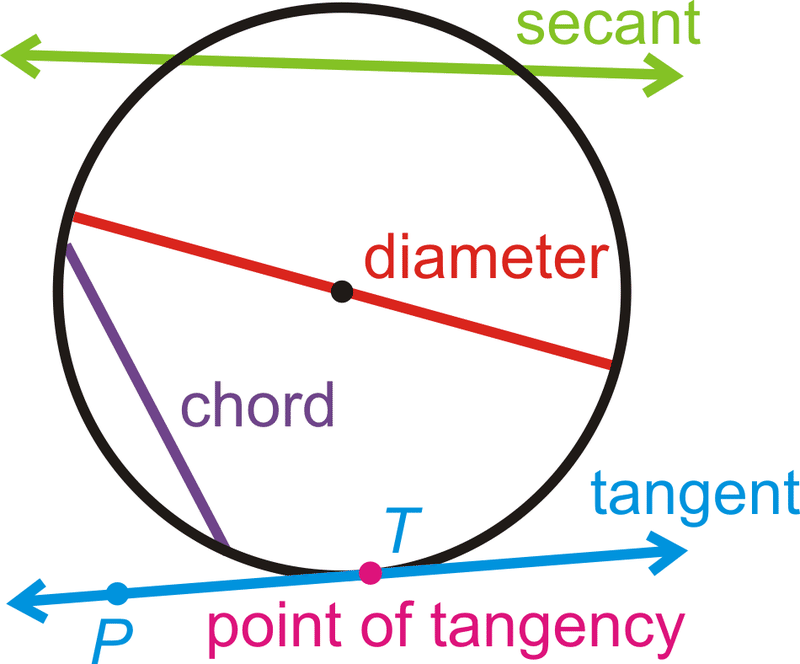
    F-D_23af70 Даф 753Ф3АФ 4301615966 ААА847 ААА44 Фе 0Б13Б4304657D9D9D9пострум+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Дотичний промінь\(\overrightarrow{TP}\) і дотичний сегмент також\(\overline{TP}\) називають тангенсами.

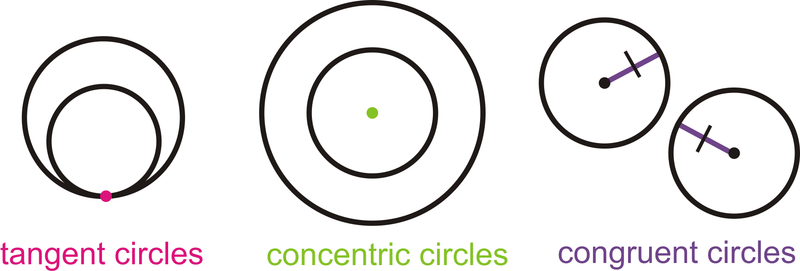
    Дотичні кола: два або більше кіл, які перетинаються в одній точці.

    Концентричні кола: два або більше кіл, які мають однаковий центр, але різні радіуси.

    конгруентних кіл: два або більше кіл з однаковим радіусом, але різним центром

    Ф-д_992Е58Ф38С0Д3БК 11Д04Ф44КБ6024589Б8КФЕ 8ДК5Е843Д0БФ2819273+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Що робити, якщо ви провели лінію через коло з одного боку в іншу, яка не проходить через центр? Що робити, якщо ви намалювали лінію поза колом, яка торкнулася кола в одній точці? Як би ви назвали ці рядки, які ви намалювали?

    Приклад\(\PageIndex{1}\)

    Знайдіть частини\(\bigodot A\), які найкраще відповідають кожному опису.

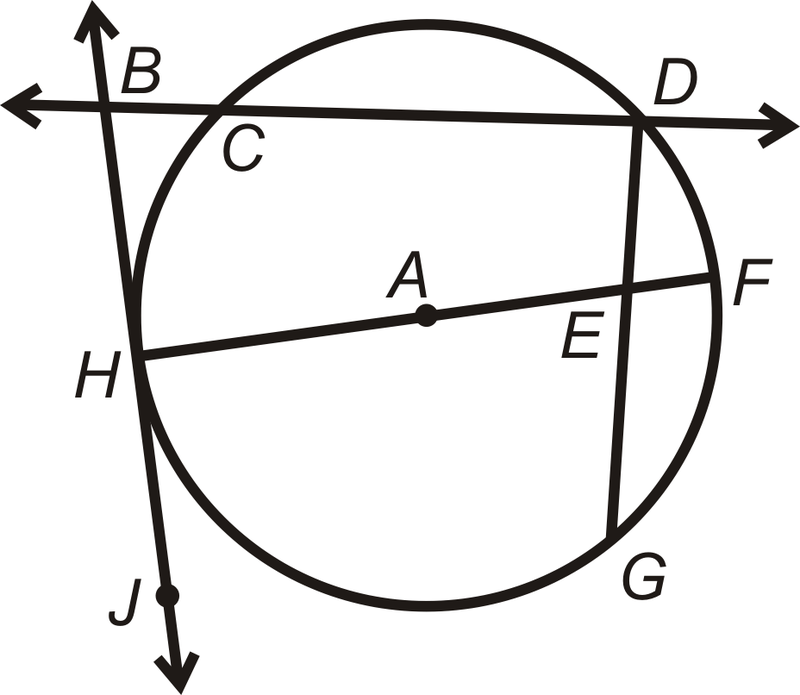
    F-д_ЕД 1ФД0980Е9 КДФ0А325АА50А7Д4Д08АФ 5Д1ЕФ55Е68А76Е6227С26303+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)
    1. Радіус A
    2. Акорд
    3. Дотична лінія
    4. Точка дотику
    5. Діаметр A
    6. Секанс

    Рішення

    1. \ оверлайн {HA}\) або\ overline {AF}\)
    2. \(\overline{CD}\),\(\overline{HF}\), або\ overline {DG}\)
    3. \(\overleftrightarrow{BJ}\)
    4. \(Point H\)
    5. \(\overline{HF}\)
    6. \(\overleftrightarrow{BD}\)

    Приклад\(\PageIndex{2}\)

    Намалюйте приклад того, як два кола можуть перетинатися з ні, одна і дві точки перетину. Ви зробите три окремих малюнка.

    Рішення

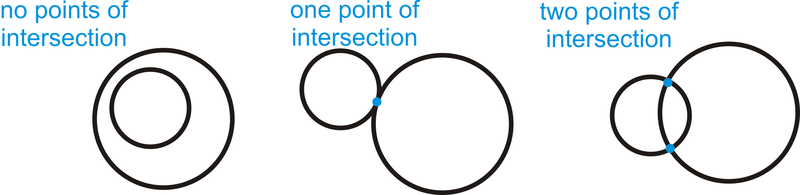
    Ф-Д_С8Б82Д3Д 3Д 33Б8Б1Д1С430ФБ894045БА40 ДБКФ 11422A97655486E54+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Приклад\(\PageIndex{3}\)

    Визначте, чи є одне з наступних кіл конгруентним.

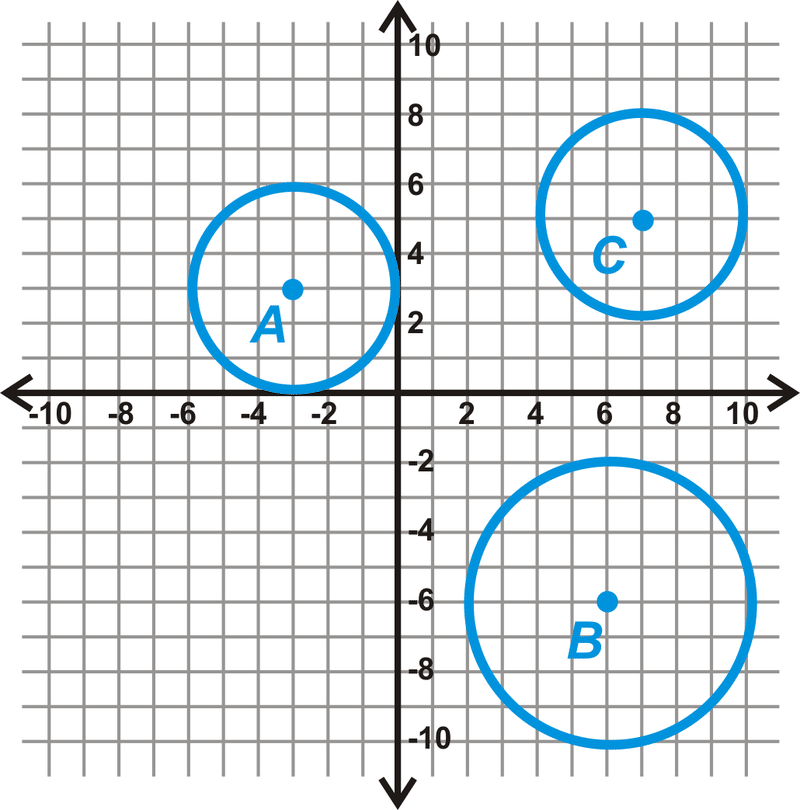
    F-D_52372F6F37212C38 постійного струму+249185628 EDC 678ЕА 0С6 ФЕД 9Б31 AB488D6D75+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    Рішення

    Від кожного центру відраховуйте одиниці до зовнішнього обідка кола. Найпростіше вважати вертикально або горизонтально. Роблячи це, ми маємо:

    \(\begin{aligned} \text{Radius of } \bigodot A&=3\text{ unit } \\ \text{Radius of } \bigodot B&=4\text{ unit }\\ \text{Radius of } \bigodot C&=3\text{ unit }\end{aligned} \)

    З цих вимірів ми бачимо, що\(\bigodot A\cong \bigodot C\).

    Зверніть увагу, що кола є конгруентними. Довжини радіусів рівні.

    Приклад\(\PageIndex{4}\)

    Чи можна мати лінію, яка тричі перетинає коло? Якщо так, намалюйте один. Якщо ні, поясніть.

    Рішення

    Це неможливо. За визначенням, всі лінії прямі. Максимальна кількість разів лінія може перетинати коло вдвічі.

    Приклад\(\PageIndex{5}\)

    Чи всі кола схожі?

    Рішення

    Так. Всі кола мають однакову форму, але не обов'язково однакового розміру, тому вони схожі.

    Рецензія

    Визначте, який термін найкраще описує кожну з наступних частин\(\bigodot P\).

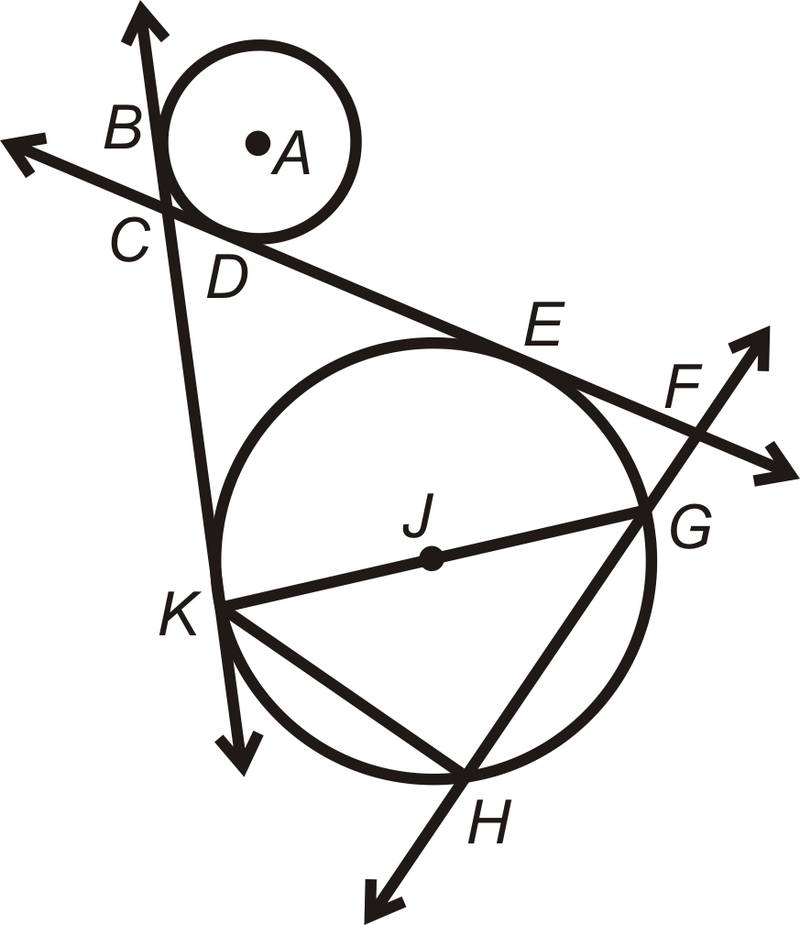
    F-D_0950Ф933Б468Б2АЕ 13828С7Ф346305ФБА 5Е41 Дек 38Б0619Ф46254Е6Б+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{7}\)
    1. \(\overline{KG}\)
    2. \(\overleftrightarrow{FH}\)
    3. \(\overline{FH}\)
    4. \(E\)
    5. \(\overleftrightarrow{BK}\)
    6. \(\overleftrightarrow{CF}\)
    7. \(A\)
    8. \(\overline{JG}\)
    9. Який найдовший акорд в будь-якому колі?

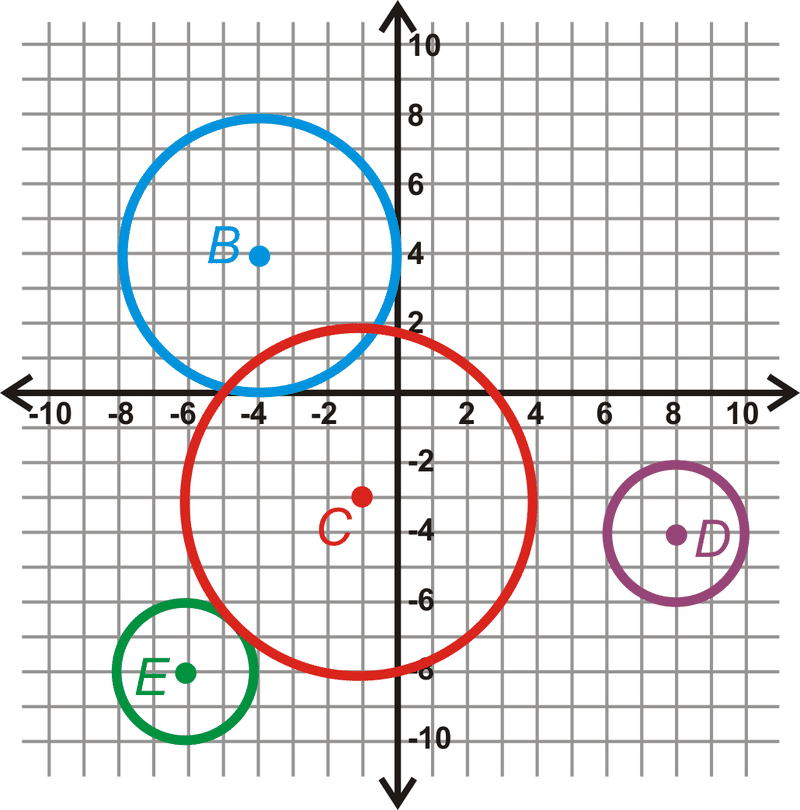
    Скористайтеся графіком нижче, щоб відповісти на наступні питання.

    1. Знайдіть радіус кожного кола.
    2. Чи є які-небудь кола конгруентними? Звідки ти знаєш?
    3. Знайти всі загальні тангенси для\(\bigodot B\) і\(\bigodot C\).
    4. \(\bigodot C\)і\(\bigodot E\) зовні дотичні. Що таке\(CE\)?
    5. Знайдіть рівняння\(\overline{CE}\).
    F-д_ФД3 СБ551714 де 9554641930 БА 7СА7 ФЕФ 050А37Б6Б9950Д0Б5Е0КАС 61+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{8}\)

    Ресурси

    Лексика

    Термін Визначення
    акорд Відрізок лінії, кінцеві точки якого знаходяться на колі.
    Коло Коло - це сукупність всіх точок на певній відстані від заданої точки в двох вимірах.
    концентричні кола Два або більше кола, які мають однаковий центр, але різні радіуси.
    конгруентні кола Два і більше кола з однаковим радіусом, але різними центрами.
    Діаметр Діаметр - це міра відстані через центр кола. Діаметр дорівнює подвоєної мірі радіуса.
    точка дотику Точка, де дотична лінія стосується кола.
    Радіус Радіус кола - це відстань від центру кола до краю кола.
    Окружність Окружність кола - це міра відстані навколо зовнішнього краю кола.
    Секантний Секанс кута в прямокутному трикутнику - це величина, знайдена діленням довжини гіпотенузи на довжину сторони, прилеглої до заданого кута. Відношення секанс - це зворотне косинусного відношення.
    Тангенс Тангенс кута в прямокутному трикутнику - це величина, знайдена діленням довжини сторони, протилежної заданому куту, на довжину сторони, прилеглої до заданого кута.
    Дотичні кола Дотичні кола - це два або більше кіл, які перетинаються в одній точці.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Вступ до кіл

    Види діяльності: Частини гуртків Дискусійні питання

    Навчальні посібники: властивості кола навчальний посібник

    Практика: Визначте компоненти кола

    Реальний світ: обхідний шлях додому