5.25: Відповідні частини конгруентних фігур

Last updated
Save as PDF

Page ID: 54780

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Визначте відповідні довжини сторін та вимірювання кута в конгруентних фігурах.

Мелвін живе в будинку, в якому багато дзеркал. Йому подобається дивитися в дзеркала і грати з дзеркалами. Одного разу його мати каже йому, що дзеркало у формі паралелограма біля вхідних дверей збігається з дзеркалом у формі паралелограма поруч із фотографіями в коридорі. Мелвін малює дві форми якнайкраще, наскільки він може, і позначає деталі, які він знає для кожної форми.

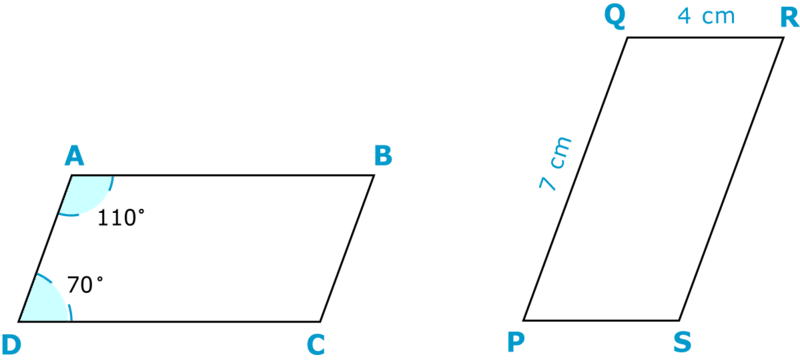
F-д_88055ф 8955 кд 88Ф0С13990796Е1Б4С6А39ЕЕЕЦ6129АА1530Б981E9C1+зображення_крихіткий+зображення_крихіткий_PNG — Малюнок\(\PageIndex{2}\)

Яка довжина\(\overline{AB}\)?

У цій концепції ви дізнаєтеся про відповідні частини конгруентних фігур.

Відповідні частини конгруентних фігур

Слово відповідне відноситься до частин, які збігаються між двома конгруентними трикутниками. Можна визначити відповідні кути і відповідні сторони.

F-д_Ф 61С8253029Д7А3Е75Ф8175ФБ05А11292С853С8253029Д7A3E44751A0902+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{3}\)

Спочатку назвіть відповідні кути. Відповідні кути - це відповідні кути між двома трикутниками. Відповідні кути матимуть однакову міру в конгруентних трикутниках.

\(\angle A\cong \angle D\angle B\cong \angle E\angle C\cong \angle F\)

Тут кути пов'язані з символом конгруентного. Коли ви бачите знак рівності з химерною лінією зверху, ви знаєте, що елементи з кожного боку рівняння є конгруентними.

Далі назвіть відповідні сторони. Відповідні сторони є відповідними сторонами між двома трикутниками. Вони будуть мати однакову довжину в конгруентних трикутниках.

\(\begin{aligned}\overline{AB}&\cong \overline{DE} \\ \overline{AC} &\cong \overline{DF} \\ \overline{BC} &\cong \overline{EF}\end{aligned}\)

Приклад\(\PageIndex{1}\)

Раніше вам давали проблему про Мелвіна і його будинку дзеркал.

Він дізнається, що два дзеркала є конгруентними, тому він малює форми якнайкраще, наскільки може, і заповнює те, що знає про кожну форму.

Яка довжина\(\overline{AB}\)?

Рішення

По-перше, поверніть другу фігуру так, щоб вона виглядала так само, як і перша фігура.

Далі визначте сторону на другому трикутнику, яка відповідає\(\overline{AB}\).

\(\overline{PQ}\)

Потім напишіть довжину відповідної сторони.

7 см

Відповідь - 7 см. Довжина 7 см.\(\overline{AB}\)

Приклад\(\PageIndex{2}\)

Ці дві фігури є конгруентними. Який кут конгруентний куту\(A\)?

Рішення

Спочатку переверніть другу фігуру так, щоб вона розташовувалася як перша фігура.

Потім визначте кут на другій фігурі, який знаходиться в тому ж положенні, що і кут\(A\) в першому трикутнику.

\(P\)

Відповідь - кут\(P\). \(\angle A\cong \angle P\)

Використовуйте наступну діаграму двох конгруентних трикутників, щоб відповісти на наступні запитання.

F-д_Ф07а 6333Б7С143 А6С7А048А027БК 7Д42БК 7Ф0А8725973636369C+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{6}\)

Приклад\(\PageIndex{3}\)

\(E\)Кут конгруентний куту _____

Рішення

Спочатку переконайтеся, що трикутники розташовані так, щоб вони виглядали однаково.

Так

Потім визначте кут на другому трикутнику, який знаходиться в тому положенні, що кут\(E\) знаходиться в першому трикутнику.

\( H\)

Відповідь - кут\(H\). \(E\)Кут конгруентний куту\(H\).

Приклад\(\PageIndex{4}\)

\(\overline{FG}\cong ______\)

Рішення

Спочатку переконайтеся, що трикутники розташовані так, щоб вони виглядали однаково.

Так

Потім визначте відрізок лінії на другому трикутнику, який знаходиться в положенні, яке\(\overline{FG}\) знаходиться в першому трикутнику.

\(\overline{IJ}\)

Відповідь є\(\overline{IJ}\). \(\overline{FG}\cong \overline{IJ}\).

Приклад\(\PageIndex{5}\)

\(J\)Кут конгруентний куту _____

Рішення

Спочатку переконайтеся, що трикутники розташовані так, щоб вони виглядали однаково.

Так

Потім визначте кут на другому трикутнику, який знаходиться в тому положенні, що кут J знаходиться в першому трикутнику.

\(G\)

Відповідь - кут\(G\). \(J\)Кут конгруентний куту\(G\).

Рецензія

Використовуйте наступні трикутники, щоб відповісти на питання.

F-д_7 ЕБА 2Б0135Д25Ф3Е2 СА5ФБ909 ДБК 6 ЕА ЕБФ 84345 дек 73803AF9C51856+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{7}\)

Ці два трикутника схожі або конгруентні?
Звідки ти знаєш?
Сторона\(DE\) конгруентна з якою іншою стороною?
Сторона\(DF\) конгруентна з якою іншою стороною?
Сторона\(EF\) конгруентна з якою іншою стороною?
Якщо довжина сторони DE дорівнює 10, яка довжина сторони\(GH\)?
Якщо довжина сторони HI становить 8, яка інша сторона також 8?

Використовуйте наведені нижче цифри, щоб відповісти на питання.

Ці дві фігури є конгруентними. Поясніть два способи, за допомогою яких можна визначити, чи є цифри конгруентними.
\(Q\)Кут конгруентний до якого іншого кута?
\(R\)Кут конгруентний до якого іншого кута?
\(S\)Кут конгруентний до якого іншого кута?
Якщо\(PQ\) 7 см, які інші сторони 7 см?
Якщо\(QR\) 4 см, які інші сторони 4 см?
Якщо кут\(D\) дорівнює 70 градусів, назвіть інший кут 70 градусів.
Якщо кут\(A\) 110 градусів, назвіть інший кут 110 градусів.

Ресурси

Лексика

Термін	Визначення
Конгруентний	Конгруентні фігури ідентичні за розміром, формою і мірою.
Кореспондент	Відповідні сторони між двома трикутниками - це сторони в одному відносному положенні.
Схожі	Дві фігури схожі, якщо вони мають однакову форму, але не обов'язково однакового розміру.

Додаткові ресурси

Відео: Конгруентні та подібні трикутники

Практика: Відповідні частини конгруентних фігур