5.4: Периметр квадратів і прямокутників

Last updated
Save as PDF

Page ID: 54757

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Використовуйте основні чотирикутники формули, щоб знайти загальні міри країв прямолінійних чотирикутників.

Знайти периметр і площу квадратів і прямокутників за допомогою формул

У Раджа є невеликий клаптик землі, який він хоче перетворити на город. Однак він хоче побудувати навколо нього невеликий паркан, перш ніж що-небудь посадити. Він знає, що площа землі становить 240 квадратних футів і що довжина однієї сторони становить 15 футів. Для того щоб побудувати паркан, йому потрібно знати ширину землі теж. Як Радж може написати і вирішити рівняння для визначення ширини свого майбутнього саду?

У цій концепції ви навчитеся знаходити периметр і площу квадратів і прямокутників за допомогою формул.

Периметр і площа квадратів і прямокутників

Формула - це метод, який, як було доведено, працює при вирішенні конкретних типів завдань.

Давайте вивчимо деякі з тих знайомих формул, дивлячись на прямокутники, квадрати, площу і периметр.

Периметр фігури - це відстань навколо фігури. Периметр - це сума всіх сторін квадрата або прямокутника. Оскільки прямокутник має два набори паралельних сторін, формула визначення периметра (\(P\)) прямокутника така:

\(P=2L+2W\)

\(L=length\: and\: W=width\)

Давайте розглянемо приклад.

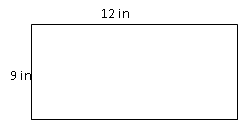
Прямокутник вище показує його розміри. Знайдіть периметр.

Спочатку підставляємо значення width (\(W\)) та length (\(L\)) у формулу периметра.

\(P=2(12)+2(9)\)

Далі завершіть множення і додавання, щоб знайти периметр.

\(\begin{aligned} P&=2(12)+2(9) \\ P&=24+18 \\ P&=42\end{aligned}\)

Відповідь - 42.

Периметр прямокутника дорівнює 42 дюймам.

Площа - це кількість квадратних одиниць всередині фігури. Площа знаходить множенням довжини\ на ширину. Формула знаходження площі прямокутника така:

\(A=L\times W\)

Ви можете використовувати розміри з прямокутника вище, щоб знайти площу цього прямокутника.

Спочатку заповніть значення для\(L\) та\(W\) у формулу для площі.

\(\begin{aligned} A&=L\times W \\ A&=12\times 9\end{aligned}\)

Далі вирішуйте для площі множенням.

\(\begin{aligned} A&=12\times 9 \\ A&=108\end{aligned}\)

Відповідь - 108.

Площа прямокутника дорівнює\(108\: in^2\).

Зверніть увагу, що одиниця виміру для площі знаходиться в квадраті. Це тому, що ви помножили одиницю виміру на себе:\(in\times in=in^2\). Площа завжди пишеться в квадратних одиницях.

Також можна знайти периметр і площу квадрата. Пам'ятайте, що квадрат має чотири рівні сторони, задані символом s. Для знаходження периметра квадрата можна скористатися наступною формулою:

\(P=4s\)

Давайте розглянемо приклад.

Прямокутник має довжину 12 футів і периметр 72 футів. Напишіть і вирішіть рівняння для визначення ширини прямокутника.

Спочатку підставляємо значення периметра (\(P\)) та length (\(L\)) у формулу периметра.

\(72=2(12)+2W\)

Далі завершуємо множення.

\(72=24+2W\)

Потім відніміть 24 з обох сторін, щоб отримати змінну поодинці з правого боку.

\(\begin{aligned} 72−24&=24−24+2W \\ 48 &=2W \end{aligned}\)

Потім помножте обидві сторони на зворотну 2, щоб ізолювати свою змінну.

\(\begin{aligned} \dfrac{1}{2}\times \dfrac{48}{1} &=\dfrac{1}{2}\times \dfrac{2W}{1} \\ \dfrac{48}{2}&=W \\ W&=24\end{aligned}\)

Відповідь - 24.

Ширина прямокутника становить 24 фути.

Приклад\(\PageIndex{1}\)

Раніше вам дали проблему з приводу Раджа і його садового паркану.

Він знає, що площа землі становить 240 квадратних футів, довжина однієї сторони - 15 футів, і потрібно знати ширину землі.

Рішення

Спочатку підставляємо значення площі та довжини сторони у формулу площі.

\(\begin{aligned} A&=L\times W \\ 240\text{ ft}^2 &=15\text{ ft } \times W\end{aligned}\)

Далі множимо обидві сторони на зворотну 15, щоб виділити змінну W.

\(\begin{aligned} \dfrac{1}{15}\times \dfrac{240}{1}&=\dfrac{1}{15}\times \dfrac{15}{1} \times W \\ W&=16 \end{aligned}\)

Відповідь - 16.

Ширина саду Раджа становить 16 футів. Тому розміри саду становлять 16 футів на 15 футів.

Приклад\(\PageIndex{2}\)

Квадрат має периметр 196 дюймів. Визначте довжину однієї сторони квадрата.

Рішення

Спочатку підставляємо значення периметра (\(P\)) в формулу периметра.

\(196=4s\)

Далі помножте обидві сторони на зворотну 4, щоб ізолювати свою змінну.

\(\begin{aligned} \dfrac{1}{4}\times \dfrac{196}{1}&=\dfrac{1}{4}\times \dfrac{4s}{1} \\ \dfrac{196}{4}&=s \\ s&=49 \end{aligned}\)

Відповідь 49.

Приклад\(\PageIndex{3}\)

Знайдіть периметр наступного квадрата, якщо довжина сторони дорівнює\(4.5\: inches\).

Рішення

Спочатку підставляємо значення довжини сторони в формулу периметра.

\(\begin{aligned} P&=4s \\ P&=4(4.5) \end{aligned}\)

Далі множимо на 4, щоб вирішити для периметра.

\(\begin{aligned} P&=4(4.5) \\ P&=18 \end{aligned}\)

Відповідь - 18.

Приклад\(\PageIndex{4}\)

Чи можете ви знайти площу квадрата в прикладі 1?

Рішення

Спочатку підставляємо значення довжини сторони в формулу площі.

\(\begin{aligned} A&=s\times s \\ A&=4.5\times 4.5 \end{aligned}\)

Далі множте, щоб вирішити для площі.

\(\begin{aligned} A&=4.5\times 4.5 \\ A&=20.25\end{aligned}\)

Відповідь - 20.25.

Площа площі становить\(20.25\text{ in}^2\).

Приклад\(\PageIndex{5}\)

Квадрат має площу 144 кв. метра. Яка довжина сторони?

Рішення

Спочатку підставляємо значення площі в формулу площі.

\(\begin{aligned} A&=s\times s \\ 144\text{ m}^2 &=s\times s \end{aligned}\)

Далі візьміть квадратний корінь ділянки для ізоляції\(s\). Пам'ятайте, що протилежність квадрату - квадратний корінь.

\(\begin{aligned} 144&=s\times s \\ 144&=s^2 \\ s&=\sqrt{144} \\ s&=12 \end{aligned}\)

Відповідь - 12.

Рецензія

Знайдіть площу і периметр кожного квадрата або прямокутника за допомогою формул і заданих розмірів. Кожна проблема матиме дві відповіді.

Квадрат з довжиною сторони 5 дюймів.
Прямокутник довжиною 5 дюймів і шириною 3 дюйми.
Прямокутник довжиною 8 см і шириною 6 см.
Квадрат з довжиною сторони 11 футів.
Прямокутник довжиною 9 дюймів і шириною 4,5 дюйма.
Квадрат з довжиною сторони 7 футів.
Прямокутник довжиною 12 метрів і шириною 11 метрів.
Квадрат з довжиною сторони 13 метрів.
Прямокутник довжиною 15 футів і шириною 8 футів.
Квадрат з довжиною сторони 12,5 футів.

Знайдіть відсутню довжину сторони, задану площу кожного квадрата.

\(A=64\text{ in}^2\)
\(A=36\text{ in}^2\)
\(A=81\text{ m}^2\)
\(A=100\text{ in}^2\)
\(A=144\text{ ft}^2\)
\(A=121\text{ cm}^2\)
\(A=4\text{ mm}^2\)

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 1.13.

Лексика

Термін	Визначення
Площа	Площа - простір в межах периметра двомірної фігури.
Формула	Формула - це тип рівняння, який показує зв'язок між різними змінними.
Периметр	Периметр - це відстань навколо двомірної фігури.
Квадратний блок	Квадратна одиниця - це квадрат з чотирма сторонами, кожен вимірює 1 одиницю.

Додаткові ресурси

Інтерактивний елемент

Відео: Визначаємо площу прямокутника за участю цілих чисел

Практика: Периметр квадратів і прямокутників

Реальний світ: Стібок у часі