Skip to main content
LibreTexts - Ukrayinska

5.24: Конгруентні багатокутники

  1. Last updated
  2. Save as PDF
  • Page ID
    54843

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Розпізнавати і розуміти конгруентні багатокутники.

    Конгруентні фігури

    F-D_8652d486583FC4176749A605AB33B418F6EC3F56F5E10267C688D8B5+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{1}\)

    Челсі хоче покласти шаховий візерунок на її шафка на день народження. Вона повинна зробити візерунок на плакатній дошці, а потім приклеїти його до її шафки, щоб вона не назавжди пошкодити її шафка. Вона вирішує, що найпростіший прийом - дістати будівельний папір і вирізати достатню кількість квадратів, щоб зробити її візерунок. Як вона може сказати, чи збігаються квадрати, які вона вирізає?

    У цьому понятті ви дізнаєтеся про конгруентних фігурах.

    Конгруентні фігури

    Конгруентні фігури мають абсолютно однакові розміри і форму. Вони мають конгруентні сторони і конгруентні кути.

    Ось кілька пар конгруентних фігур.

    F-д_268ФБ81Ф75Б132ЕФ5КС313Е299Д5А68FF9E00D96C665D70 бісер FC98D+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Порівняйте цифри в кожній парі. Вони точно такі ж. Якщо ви не впевнені, уявіть, що ви могли б вирізати одну фігуру і розмістити її поверх іншої. Якщо вони точно збігаються, вони конгруентні.

    Перевірте на конгруентність, порівнявши кожну сторону і кут двох фігур. Кожна сторона і кут однієї фігури відповідають стороні або куту в іншій. Вони називаються відповідними частинами. Наприклад, верхня точка одного трикутника відповідає верхній точці іншого трикутника в конгруентній парі.

    Не завжди легко побачити відповідні частини двох фігур. Одна фігура може повертатися по-різному, щоб відповідні частини виявилися в різних місцях. Якщо ви не впевнені, простежте одну фігуру і помістіть її поверх іншої, щоб побачити, чи зможете ви зробити їх збігатися.

    Чи є пара фігур нижче конгруентної?

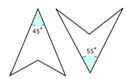
    F-D_B89БК353C1517251F02B036CE407E4FB7294878578E55D3699F9B0A1+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_jpg
    Малюнок\(\PageIndex{3}\)

    Спочатку подивіться на форму кожної фігури.

    Форми виглядають аналогічно.

    Далі визначте, чи є відповідні деталі.

    Задані кути не відповідають тому, що вони мають різні значення.

    Потім визначте, чи відповідають фігури.

    Ні.

    Відповідь полягає в тому, що пара фігур не конгруентна.

    Ви можете використовувати інформацію про одну фігуру в парі конгруентних фігур, щоб знайти міру відповідного кута або сторони в іншій фігурі. Давайте подивимося, як це працює. Погляньте на конгруентні цифри нижче.

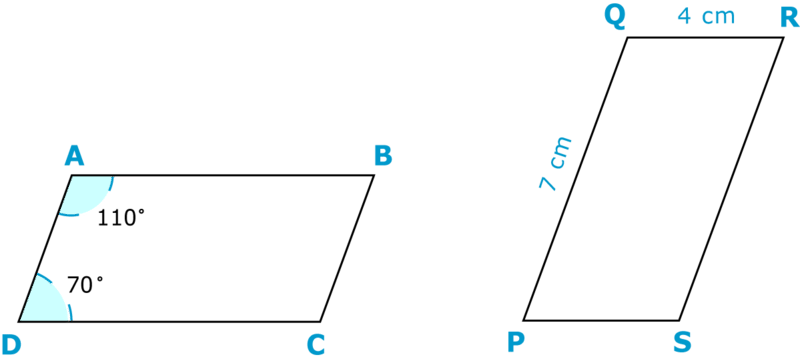
    F-д_88055ф 8955 кд 88Ф0С13990796Е1Б4С6А39ЕЕЕЦ6129АА1530Б981E9C1+зображення_крихіткий+зображення_крихіткий_PNG
    Малюнок\(\PageIndex{4}\)

    Ці два паралелограми є конгруентними. Знайдіть відповідні деталі.

    Спочатку проведіть один паралелограм і помістіть його поверх іншого. Повертайте його до тих пір, поки деталі не відповідають.

    Ви можете бачити, що сторона\(AB\) відповідає стороні,\(PQ\) тому що вони конгруентні. Тому,

    \(AB\cong PQ\).

    Перерахуйте всі конгруентні сторони.

    \(\begin{aligned} AB&\cong PQ \\ BC &\cong QR \\ AD&\cong PS \\ DC &\cong SR \end{aligned}\)

    Перерахуйте конгруентні кути.

    \(\begin{aligned}\angle A &\cong \angle P \qquad& \angle D&\cong \angle S \\ \angle B &\cong \angle Q \qquad& \angle C&\cong \angle R \end{aligned}\)

    Тепер знайдемо довжину сторони\(AB\).

    \(AB\)є конгруентною\(PQ\), тому, якщо ви знайдете довжину,\(PQ\) то вона буде однаковою для\(AB\). \(PQ\)становить 7 сантиметрів. Тому AB також повинен бути довжиною 7 сантиметрів.

    Тепер давайте подивимося на кути. Давайте знайдемо міру\(\angle C\). Кут відповідає\ кут R, але ви не знаєте міру\(\angle R\) жодного. Однак ви знаєте міри двох кутів у першому паралелограмі:\(70^{\circ}\) і\(110^{\circ}\). Ви не знаєте міру\ кута B, але цього разу ви знаєте міру відповідного кута,\(\angle Q\). Ці два кути є конгруентними, тому ви знаєте, що\ кут B повинен вимірювати\(70^{\circ}\). Тепер ви знаєте три кути на першому малюнку, так що ви можете відняти, щоб знайти міру\(\angle C\).

    \(\begin{aligned} 360−(70+110+70) &=\angle C \\ 360−250&=\angle C \\ 110^{\circ}&=\angle C \end{aligned}\)

    Приклад\(\PageIndex{1}\)

    Раніше вам дали проблему про Челсі та її шаховій тематичній шафці.

    Вона вирізала форми, як вона може сказати, чи збігаються квадрати, які вона вирізала?

    Рішення

    Спочатку виміряйте довжини сторін.

    Всі сторони рівні.

    Далі виміряйте кути.

    Всі кути повинні бути рівними.

    Потім зробіть висновок.

    Форми конгруентні.

    Відповідь полягає в тому, що форми конгруентні.

    Приклад\(\PageIndex{2}\)

    Чи є пара нижче конгруентної?

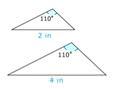
    F-D_8673B9A35DA88A978F55C8C8150453C0А43Е37Ф13C245D3BB2A2AFD6+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_jpg
    Малюнок\(\PageIndex{5}\)

    Рішення

    Спочатку подивіться на форму кожної фігури.

    Форми виглядають аналогічно, але одна форма менша за іншу.

    Далі визначте, чи є відповідні деталі.

    Здається, є відповідні кути, але сторони, які знаходяться в одному положенні, не є конгруентними.

    Потім визначте, чи відповідають форми.

    Ні.

    Відповідь полягає в тому, що пара фігур не конгруентна.

    Приклад\(\PageIndex{3}\)

    Чи є пара фігур конгруентною?

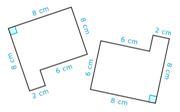
    F-D_25821669Ф3432Ф36Е73Е6ФД ДЕ 6763ФА55178C2B4717DB2481B10BFE2+зображення_thumb_поштова листівка_крихітка_зображення_великий палецька_листівка_крихітка_jpg
    Малюнок\(\PageIndex{6}\)

    Рішення

    Спочатку подивіться на форму кожної фігури.

    Форми виглядають аналогічно.

    Далі визначте, чи є відповідні деталі.

    Здається, є відповідні кути, але не всі сторони, які знаходяться в одному положенні, є конгруентними.

    Потім визначте, чи відповідають форми.

    Ні.

    Відповідь полягає в тому, що пара фігур не конгруентна.

    Приклад\(\PageIndex{4}\)

    Що таке міра\(\angle M\)?

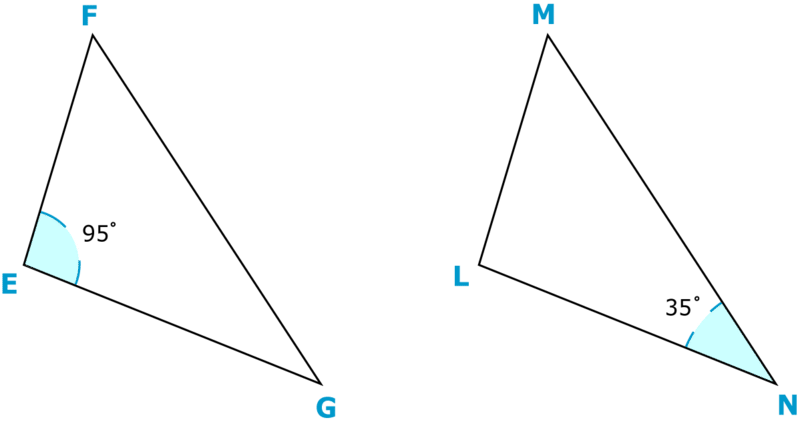    Ф-д_6е31д166436С8 АБББ 84С80С1БК 56213А89С3Б00Б0241067Е953Б9Ф47+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{7}\)

    Рішення

    Спочатку визначте кут, який відповідає куту\(L\).

    \(Angle L = Angle E = 95^{\circ}\)

    Далі зрозумійте, що сума трьох внутрішніх кутів становить 180o і напишіть рівняння.

    \(95+35+x=180\)

    Потім вирішіть для відсутнього кута вимірювання.

    \(\begin{aligned} 130+x&=180 \\ x&=50 \end{aligned}\)

    Відповідь полягає в тому, що міра кута М є\(50^{\circ}\).

    Приклад\(\PageIndex{5}\)

    \(DEF\)Трикутник конгруентний з трикутником\(KLM\). Якщо\(angle D=42^{\circ}\), яка міра кута\(K\)?

    Рішення

    По-перше, визначити, чи\(K\) є кут конгруентний куту\(D\).

    Так, так і є.

    Далі слід згадати взаємозв'язок між конгруентними частинами.

    Конгруентні частини рівні.

    Потім напишіть міру кута\(K\).

    \(42^{\circ}\)

    Відповідь полягає в тому, що кут\(K=42^{\circ}\).

    Рецензія

    Назвіть відповідні частини тим, які наведені нижче.

    F-D_1F0DAB88064E7993cd372B0424E8909E0d2b1B418E70805B3B2D055C+зображення_thumb_поштова листівка_крихітка+зображення_thumb_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{8}\)
    1. \(\angle R\)
    2. \(MN\)
    3. \(\angle O\)

    Використовуйте зв'язки між конгруентними фігурами, щоб знайти міру\(g\). Покажіть свою роботу.

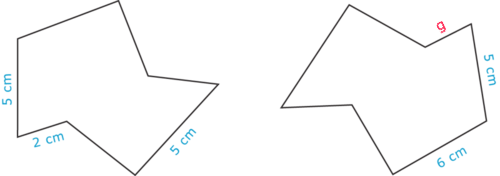
    1. F-D_B5a5359B1753650 Бабб 3d1c64bffec219f0484483356F70b53755E56+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png
      Малюнок\(\PageIndex{9}\)

    Використовуйте зв'язки між конгруентними фігурами, щоб знайти міру\(\angle T\). Покажіть свою роботу.

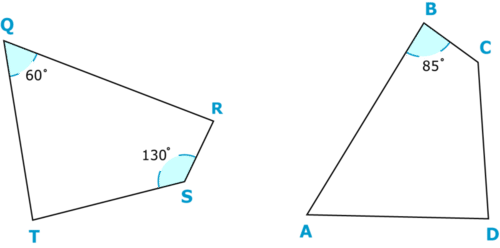
    1. F-D_7C6D504DE505613643DA55800 DAAC F7F23263F6E7FF018FBA3085F12+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png
      Малюнок\(\PageIndex{10}\)

    Дайте відповідь на кожне з наступних питань.

    1. Трикутники\(ABC\) і\(DEF\) є конгруентними. Якщо міра кута А є\(58^{\circ}\), яка міра кута,\(D\) якщо вона відповідає куту\(A\)?
    2. Правда чи брехня. Конгруентні фігури абсолютно однакові у всіх відношеннях.

    Визначте дані трикутники як візуально конгруентні чи ні.

    1. F-д_4е739Б5Ф2Д24212690Б757688Ф1Б3С0С6273ДК6Ф305123C98F467+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{11}\)
    2. F-D_415ЕДА 808Б74Д999ФБ2 ЕАД 0372Ф9ДБ Б Б 7Б1СА70387ФД8Е03А7356+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)
    3. F-д_88ФДБ 3ДБФ 98А48062С7Бакд БД0БД 0Б0884Д758692ФЦ51ФК12347Б2А+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)
    4. F-D_0FF2E5183D8245 змінного струму 5A4A2486C53 BE38169B83F Кабель 043D87265E36+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{14}\)
    5. F-D_6B 656893 ЕАД 7А4844 ЕД2Д2С8А95Ф34613Б90353Ф720КФ2Б8А8CF+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{15}\)

    Дайте відповідь на кожне з наступних питань.

    1. Трикутники\(ABC\) і\(DEF\) є конгруентними. Чи означає це, що їх кутові заходи однакові? Чому?
    2. Визначте конгруентний.
    3. Правда чи брехня. Якщо дві фігури конгруентні, то вони мають однакові сторони довжини, але не однакові кутові заходи.
    4. Трикутники\(ABC\) і\(DEF\) є конгруентними. Якщо міра кута А є\(58^{\circ}\), яка міра кута D, якщо вона відповідає куту А?

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 8.12.

    Ресурси

    Лексика

    Термін Визначення
    Кут Геометрична фігура, утворена двома променями, які з'єднуються в одній точці або вершині.
    Конгруентний Конгруентні фігури ідентичні за розміром, формою і мірою.
    Трапеція Трапеція - це чотирикутник з рівно однією парою паралельних протилежних сторін.
    Жорстке перетворення Жорстке перетворення - це перетворення, яке зберігає відстань і кути, воно не змінює розмір або форму фігури.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Конгруентні та подібні трикутники

    Практика: Конгруентні багатокутники

    Реальний світ: Копікати