Skip to main content
LibreTexts - Ukrayinska

5.26: Визначте відсутні кутові заходи

  1. Last updated
  2. Save as PDF
  • Page ID
    54768

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Знайти відсутні кутові міри чотирикутників за сумою 360 градусів.

    Розуміння кутових мір чотирикутників

    F-D_EE304FB8E80241E65E5CEFF9ФБ1Е16А3614Б333ФАБ3FAB3ECF7F16132+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_jpg
    Малюнок\(\PageIndex{1}\)

    Стефані, студентка з математики 12, допомагає зібрати гроші для участі в цьогорічній олімпіаді з математики в Далласі, штат Техас. Оскільки Стефані дуже артистична у виготовленні ювелірних виробів, вона вирішила виготовляти та продавати намиста, щоб зібрати гроші. Кілька клієнтів запитали її, яку форму вона використовувала для синьої намистини особливо геометричного вигляду намиста. Вона знає, що це за форма, але не впевнена, як пояснити цю форму своїм клієнтам.

    Що Стефані може розповісти своїм клієнтам про цю форму?

    У цій концепції ви навчитеся розуміти кутові міри чотирикутників.

    Чотирикутники

    Чотирикутник - це двомірна замкнута форма, яка має чотири прямі сторони.

    Три спеціальні чотирикутники - це паралелограм, який є чотирикутником з протилежними сторонами паралельно і конгруентно, трапеція, яка є чотирикутником, який має одну пару протилежних сторін паралельно і повітряний змій, який є чотирикутником, який має дві пари конгруентні суміжні сторони.

    Три спеціальні паралелограми - це прямокутник, який має кожен кут, прямий кут і протилежні сторони, як конгруентні, так і паралельні, квадрат, який має кожен кут, прямий кут, протилежні сторони паралельні і всі сторони конгруентні і ромб, який має кожну сторону, рівну довжина, протилежні сторони паралельні, але не кожен кут є прямим кутом.

    Пам'ятайте, чотирикутник - це двовимірна замкнута форма, яка має чотири прямі сторони і чотири кути.

    Сума внутрішніх кутів чотирикутника\(360^{\circ}\) незалежно від типу чотирикутника. На наступній схемі будуть показані різні чотирикутники і їх внутрішні кути.

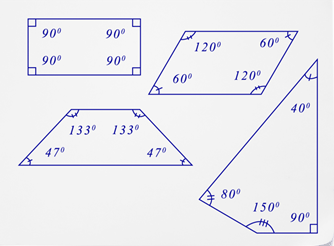
    F-D_1466688CA0781 CF307269БК018Ф8Б3БД346Ф8Е8ФДБ44А5CF0BF8E61CF+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{2}\)

    Якщо додати міру чотирьох внутрішніх кутів кожного чотирикутника, показаного вище, сума буде дорівнює\(360^{\circ}\). Кожен з цих чотирикутників можна розділити на два трикутника. Запам'ятайте, що сума внутрішніх кутів трикутника дорівнює\(180^{\circ}\). Якщо замкнута фігура містить два трикутника, то сума внутрішніх кутів дорівнює\(2(180^{\circ})=360^{\circ}\).

    Давайте застосуємо ці факти до прикладу.

    Для наступного чотирикутника визначте міру\ кут M\).

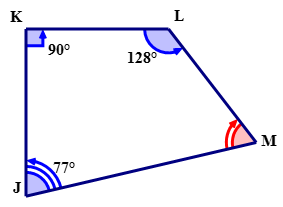
    F-D_213 ліжко 05ed7071f6d492975036a6f295e5920F6A927E8A1B8DB9958+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{3}\)

    Спочатку напишіть рівняння, яке відображає суму внутрішніх кутів чотирикутника\(JKLM\).

    \(\angle J+\angle K+\angle L+\angle M=360^{\circ}\)

    Далі підставляємо в рівняння задані міри кутів J\), K\) і L\).

    \(\begin{aligned} \angle J+\angle K+\angle L+\angle M &=360^{\circ} \\ 77^{\circ}+90^{\circ}+128^{\circ}+\angle M &=360^{\circ} \end{aligned}\)

    Далі спрощуємо ліву частину рівняння.

    \(\begin{aligned}77^{\circ}+90^{\circ}+128^{\circ}+\angle M&=360^{\circ} \\ 295^{\circ}+\angle M&=360^{\circ}\end{aligned}\)

    Потім відніміть\(295^{\circ}\) з обох сторін рівняння, щоб вирішити для міри\(\angle M\).

    \(\begin{aligned} 295^{\circ}+\angle M &=360^{\circ} \\ 295^{\circ}−295^{\circ}+\angle M &=360^{\circ}−295^{\circ} \\ \angle M &=65^{\circ} \end{aligned}\)

    Відповідь - 65.

    Міра\(\angle M\) є\(65^{\circ}\).

    Цей метод може бути використаний для обчислення міри відсутнього кута будь-якого чотирикутника, коли відомі міри трьох кутів.

    Приклад\(\PageIndex{1}\)

    Раніше вам давали проблему про Стефані та її намиста. Їй потрібно розібратися, що розповісти своїм покупцям про форму синьої намистини. Що вона може їм розповісти?

    Рішення

    Спочатку намалюйте форму і включіть всі важливі позначки.

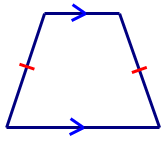
    F-D_5BB12854344E02AFDD4BF660317AF0B8746D4FD1C7C4D07962BC1F+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{4}\)

    Далі поясніть розмітку з боків фігури.

    Стрілки на верхній і нижній сторонам фігури вказують на те, що ця пара протилежних сторін паралельна. Мітка tic з двох інших сторін вказує на те, що ці сторони конгруентні (рівні по довжині).

    Потім назвіть фігуру.

    Форма синьої намистини - рівнобедрений трапеція.

    Приклад\(\PageIndex{2}\)

    Чотирикутник,\(ABCD\) що має одну пару протилежних сторін паралельно, має кутові заходи такі, що\(\angle A=44^{\circ}\). Знайдіть міру\(\angle C\) в наступному чотирикутнику.

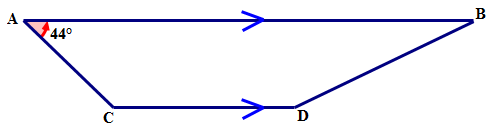
    F-D_649C81525D29669085B6C742043A1FCE165752DF11920dbe48283499+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{5}\)

    Рішення

    Спочатку назвіть тип чотирикутника і запишіть те, що ви знаєте.

    Чотирикутник з однією парою протилежних сторін паралельно називається трапецією. \(\angle A\)і\(\angle C\) знаходяться на одній стороні ноги\(\angle AC\) і є додатковими.

    Далі напишіть рівняння, щоб змоделювати те, що ви знаєте про два кути.

    \(\angle A+\angle C=180^{\circ}\)

    Далі заповнюємо в рівняння міру\(\angle A\).

    \(\begin{aligned} \angle A+\angle C&=180^{\circ} \\ 44^{\circ}+\angle C&=180^{\circ}\end{aligned}\)

    Потім відніміть\(44^{\circ}\) з обох сторін рівняння для вирішення для\ кута C\).

    \(\begin{aligned} 44^{\circ}+\angle C&=180^{\circ} \\ 44^{\circ}−44^{\circ}+\angle C&=180^{\circ}−44^{\circ} \\ \angle C &=136^{\circ} \end{aligned}\)

    Відповідь - 136.

    Міра\(\angle C\) є\(136^{\circ}\).

    Приклад\(\PageIndex{3}\)

    Для наступного чотирикутника знайдіть міру невідомого кута.

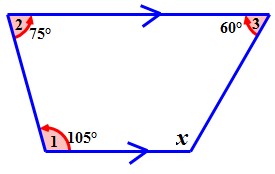
    F-D_47348A3B0094CB8F1ACFF0702FF2EA370D7DBE0AB7B2DB000b4CEC2D+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{7}\)

    Рішення

    Спочатку напишіть рівняння для моделювання суми внутрішніх кутів чотирикутника.

    \(\angle 1+\angle 2+\angle 3+\angle 4=360^{\circ}\)

    Далі заповнюємо в рівняння мірки будь-яких відомих кутів.

    \(\begin{aligned} \angle 1+\angle 2+\angle 3+\angle 4 &=360^{\circ} \\ 105^{\circ}+75^{\circ}+60^{\circ}+\angle 4&=360^{\circ} \end{aligned}\)

    Далі нехай\(\angle 4=x\)

    \(\begin{aligned} 105^{\circ}+75^{\circ}+60^{\circ}+\angle 4=360^{\circ} \\ 105^{\circ}+75^{\circ}+60^{\circ}+x=360^{\circ} \end{aligned}\)

    Далі спрощуємо ліву частину рівняння.

    \(\begin{aligned}105^{\circ}+75^{\circ}+60^{\circ}+x&=360^{\circ} \\ 240^{\circ}+x&=360^{\circ} \end{aligned}\)

    Далі відніміть\(240^{\circ}\) з обох сторін рівняння, яке потрібно вирішити для '\(x\)'.

    \(\begin{aligned} 240^{\circ}+x&=360^{\circ} \\ 240^{\circ}−240^{\circ}+x&=360^{\circ} \\ x&=360^{\circ}−240^{\circ}=120^{\circ} \end{aligned}\)

    Відповідь - 120.

    Міра\(\angle 4\) є\(120^{\circ}\).

    Приклад\(\PageIndex{4}\)

    Яка міра четвертого кута чотирикутника, який має три кути, які вимірюють\(110^{\circ}\),\(80^{\circ}\) і\(95^{\circ}\)?

    Рішення

    Спочатку напишіть рівняння для моделювання суми внутрішніх кутів чотирикутника.

    \(\angle 1+\angle 2+\angle 3+\angle 4=360^{\circ}\)

    Далі заповніть в рівняння міри трьох відомих кутів.

    \(\begin{aligned} \angle 1+\angle 2+\angle 3+\angle 4&=360^{\circ} \\ 110^{\circ}+95^{\circ}+80^{\circ}+\angle 4&=360^{\circ}\end{aligned}\)

    Далі спрощуємо ліву частину рівняння.

    \(\begin{aligned} 110^{\circ}+95^{\circ}+80^{\circ}+\angle 4&=360^{\circ} \\ 285^{\circ}+\angle 4&=360^{\circ} \end{aligned}\)

    Потім відніміть\(285^{\circ}\) з обох сторін рівняння, щоб вирішити для міри\(\angle 4\).

    \(\begin{aligned} 285^{\circ}+\angle 4 &=360^{\circ} \\ 285^{\circ}−285^{\circ}+\angle 4&=360^{\circ}−285^{\circ} \\ \angle 4&=75^{\circ} \end{aligned}\)

    Приклад\(\PageIndex{5}\)

    Як називається чотирикутник, у якого всі сторони рівні по довжині, протилежні сторони паралельні, а кожен кут - прямий кут?

    Рішення

    Спочатку намалюйте чотирикутник, щоб представити інформацію, надану в задачі.

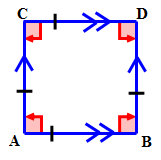
    F-D_E18 ФБ86Д6192 EA6E490FCD8694470274CBD3A8AED5048221674D80+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{8}\)

    Потім назвіть чотирикутник.

    Це спеціальний паралелограм, який називається квадратом.

    Рецензія

    Використовуйте те, що ви дізналися про чотирикутники, щоб з'ясувати відсутню міру кута кожного чотирикутника на основі трьох заданих кутів.

    1. \(120^{\circ}, 120^{\circ}, 60^{\circ}, ?\)
    2. \(50^{\circ}, 70^{\circ}, 130^{\circ}, ?\)
    3. \(52^{\circ}, 128^{\circ},52^{\circ}, ?\)
    4. \(47^{\circ}, 55^{\circ}, 120^{\circ}, ?\)
    5. \(80^{\circ}, 80^{\circ}, 100^{\circ}, ?\)
    6. \(105^{\circ}, 105^{\circ}, 85^{\circ}, ?\)
    7. \(97^{\circ}, 97^{\circ}, 35^{\circ}, ?\)
    8. \(120^{\circ}, 120^{\circ}, 40^{\circ}, ?\)
    9. \(88^{\circ}, 90^{\circ}, 60^{\circ}, ?\)
    10. \(25^{\circ}, 85^{\circ}, 85^{\circ}, ?\)
    11. \(90^{\circ}, 90^{\circ}, 90^{\circ}, ?\)
    12. \(140^{\circ}, 150^{\circ}, 45^{\circ}, ?\)
    13. \(80^{\circ}, 80^{\circ}, 120^{\circ}, ?\)
    14. \(75^{\circ}, 95^{\circ}, 110^{\circ}, ?\)
    15. \(80^{\circ}, 50^{\circ}, 95^{\circ}, ?\)

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 6.8.

    Лексика

    Термін Визначення
    Конгруентний Конгруентні фігури ідентичні за розміром, формою і мірою.
    Паралелограм Паралелограм - це чотирикутник з двома парами паралельних сторін.
    Чотирикутник Чотирикутник - замкнута фігура з чотирма сторонами і чотирма вершинами.
    Прямокутник Прямокутник - це чотирикутник з чотирма прямими кутами.
    Ромб Ромб - це чотирикутник з чотирма конгруентними сторонами.
    Квадрат Квадрат - це багатокутник з чотирма конгруентними сторонами і чотирма прямими кутами.
    Трапеція Трапеція - це чотирикутник з рівно однією парою паралельних протилежних сторін.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: властивості чотирикутника

    Практика: Визначте відсутні кутові заходи