5.22: Площа та периметр подібних багатокутників

Last updated
Save as PDF

Page ID: 54835

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Співвідношення площ - квадрат масштабного коефіцієнта; відношення периметрів - коефіцієнт масштабу.

Багатокутники схожі, коли їх відповідні кути рівні, а відповідні сторони знаходяться в однаковій пропорції. Подібно до того, як їх відповідні сторони знаходяться в однаковій пропорції, периметри та області подібних багатокутників мають особливе співвідношення.

Периметри: Співвідношення периметрів таке ж, як коефіцієнт масштабу. По суті, співвідношення будь-якої частини двох подібних форм (діагоналей, медіанів, середніх сегментів, висот і т.д.) таке ж, як і масштабний коефіцієнт.

Області: Якщо масштабний коефіцієнт сторін двох подібних багатокутників дорівнює\(\dfrac{m}{n}\), то співвідношення площ дорівнює\(\left(\dfrac{m}{n}\right)^2\) (Теорема про площу подібних полігонів). Ви квадрат співвідношення, тому що площа є двовимірним виміром.

F-D_090 CFD 653D7330C6 ЕД9143Ф65ЕААК 82561A0 ЕАБ 25D2573AE271 ДДБ+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{1}\)

Що робити, якщо вам дали два подібних трикутника і розповіли, який коефіцієнт масштабу їх сторін? Як можна було знайти співвідношення їх периметрів і співвідношення їх площ?

Приклад\(\PageIndex{1}\)

Два прямокутника нижче схожі. Знайдіть масштабний коефіцієнт і співвідношення периметрів і переконайтеся, що два результати однакові.

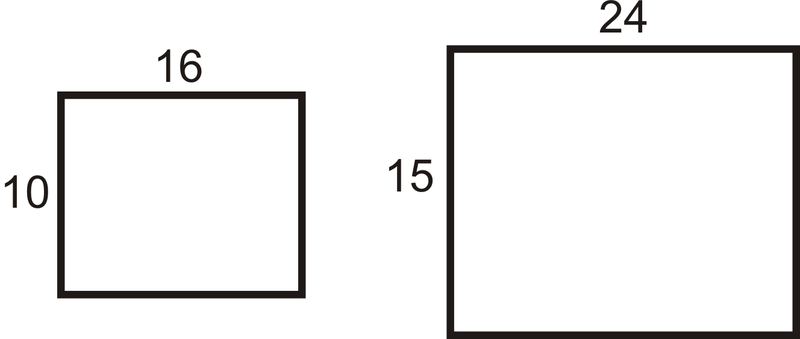
F-D_27FA42AED5E61CE4806F9E452462C85566437D5БФ 576КББ ББББ БББ 4953+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

Рішення

Коефіцієнт масштабування є\(\dfrac{16}{24}=\dfrac{2}{3}\).

\(\begin{aligned}P_{\text{ small}}=2(10)+2(16)=52\text{ units }\\ P_{\text{ large}}=2(15)+2(24)=78\text{ units }\end{aligned}\)

Співвідношення периметрів дорівнює\(\dfrac{52}{78}=\dfrac{2}{3}\).

Приклад\(\PageIndex{2}\)

Знайдіть площу кожного прямокутника з Прикладу 1. Потім знайдіть співвідношення площ і переконайтеся, що воно відповідає теоремі про площу подібних полігонів.

Рішення

\(\begin{aligned} A_{\text{ small}}&=10\cdot 16=160\text{ units}^2 \\ A_{\text{ large}}&=15\cdot 24=360\text{ units}^2 \end{aligned}\)

Співвідношення площ було б\(\dfrac{160}{360}=\dfrac{4}{9}\).

Співвідношення сторін, або масштабний коефіцієнт є\(\dfrac{2}{3}\) і співвідношення площ є\(\dfrac{4}{9}\). Зверніть увагу, що співвідношення площ - це квадрат масштабного коефіцієнта.

Приклад\(\PageIndex{3}\)

Знайти співвідношення площ ромба нижче. Ромби схожі.

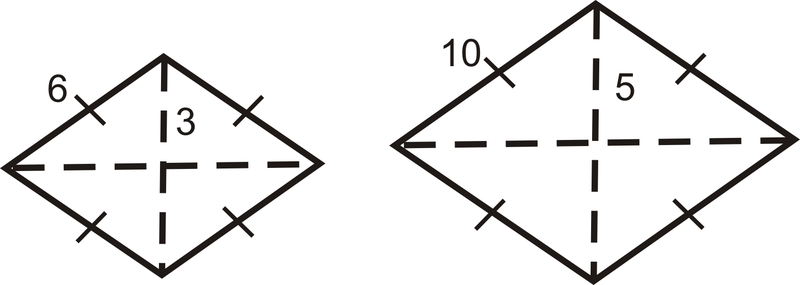
F-D_CE5676460 ДФ 1АА3Б1А43 ДБ418С9608Е49Ф34А7А4 ЕЕ4 С769ЕА64Ф9+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{3}\)

Рішення

Знайдіть співвідношення сторін і квадрат його.

\(\left(\dfrac{3}{5}\right)^2=\dfrac{9}{25}\)

Приклад\(\PageIndex{4}\)

Дві трапеції схожі. Якщо масштабний коефіцієнт дорівнює 34, а площа меншої трапеції дорівнює\(81\text{ cm }^2\), яка площа більшої трапеції?

Рішення

По-перше, співвідношення площ є\(\left(\dfrac{3}{4}\right)^2=\dfrac{9}{16}\). Тепер нам знадобиться площа більшої трапеції. Щоб знайти це, налаштуйте пропорцію, використовуючи співвідношення площі.

\(\begin{aligned}\dfrac{9}{16}=\dfrac{81}{A} \rightarrow 9A&=1296 \\ A&=144\text{ cm }^2 \end{aligned}\)

Приклад\(\PageIndex{5}\)

Два трикутника схожі. Співвідношення площ становить\(\dfrac{25}{64}\). Що таке масштабний коефіцієнт?

Рішення

Коефіцієнт масштабування є\(\sqrt{\dfrac{25}{64}}=\dfrac{5}{8}\).

Приклад\(\PageIndex{6}\)

Використовуючи співвідношення з Прикладу 5, знайдіть довжину підстави меншого трикутника, якщо довжина основи більшого трикутника дорівнює 24 одиницям.

Рішення

Налаштуйте пропорцію за допомогою масштабного коефіцієнта.

\(\begin{aligned}\dfrac{5}{8}=\dfrac{b}{24} \rightarrow 8b&=120 \\ b&=15\text{ units } \end{aligned}\)

Рецензія

Визначте співвідношення площ, враховуючи співвідношення сторін багатокутника.

\(\dfrac{3}{5}\)
\(\dfrac{1}{4}\)
\(\dfrac{7}{2}\)
\(\dfrac{6}{11}\)

Визначте співвідношення сторін багатокутника, враховуючи співвідношення площ.

\(\dfrac{1}{36}\)
\(\dfrac{4}{81}\)
\(\dfrac{49}{9}\)
\(\dfrac{25}{144}\)

Це рівносторонній трикутник, що складається з 4 конгруентних рівносторонніх трикутників.

Яке відношення площ великого трикутника до одного з малих трикутників?

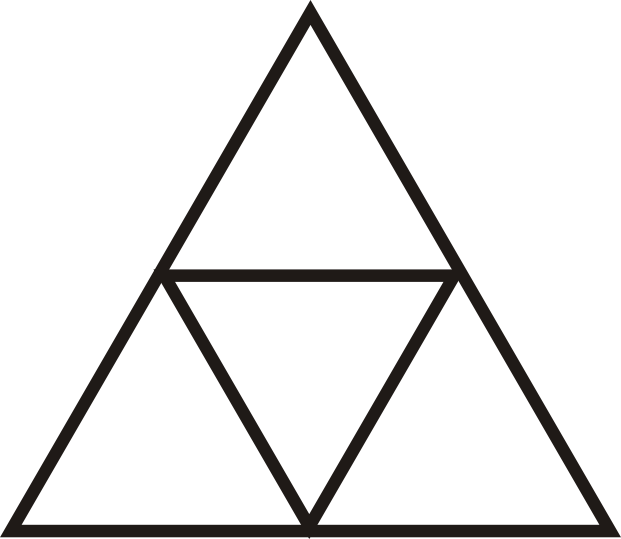
Малюнок\(\PageIndex{4}\)
Що таке масштабний коефіцієнт великого до малого трикутника?
Якщо площа великого трикутника є\(20\text{ units }^2\), яка площа малого трикутника?
Якщо довжина висоти маленького трикутника дорівнює\(2\sqrt{3}\), знайдіть периметр великого трикутника.

Малюнок\(\PageIndex{5}\)
Знайдіть периметр великого квадрата і синього квадрата.
Знайдіть масштабний коефіцієнт синього квадрата та великого квадрата.
Знайдіть співвідношення їх периметрів.
Знайдіть площу синіх і великих квадратів.
Знайдіть співвідношення їх площ.
Знайдіть довжину діагоналей синього і великого квадратів. Викладіть їх в пропорцію. Яке співвідношення таке ж, як?
Два прямокутника схожі з масштабним коефіцієнтом\(\dfrac{4}{7}\). Якщо площа більшого прямокутника дорівнює\(294\text{ in }^2\), знайдіть площу меншого прямокутника.
Два трикутника схожі з масштабним коефіцієнтом\(\dfrac{1}{3}\). Якщо площа меншого трикутника дорівнює\(22\text{ ft }^2\), знайдіть площу більшого трикутника.
Співвідношення площ двох подібних квадратів дорівнює\(\dfrac{16}{81}\). Якщо довжина сторони меншого квадрата дорівнює 24 одиницям, знайдіть довжину сторони в більшому квадраті.
Співвідношення площ двох прямих трикутників дорівнює\(\dfrac{4}{9}\). Якщо довжина гіпотенузи більшого трикутника дорівнює 48 одиницям, знайдіть довжину гіпотенузи меншого трикутника.

Питання 23-26 відбудовують один від одного. Ви можете припустити, що проблеми пов'язані.

Два подібних ромба мають області\(72\text{ units }^2\) і\(162\text{ units }^2\). Знайдіть співвідношення площ.
Знайдіть масштабний коефіцієнт.
Діагоналі в цих ромбах конгруентні. Знайдіть довжину діагоналей і сторін.
До якого типу ромбів відносяться ці чотирикутники?

Огляд (Відповіді)

Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 10.7.

Лексика

Термін	Визначення
площа	Обсяг простору всередині фігури. Площа вимірюється в квадратних одиницях.
Периметр	Периметр - це відстань навколо двомірної фігури.
Пропорція	Пропорція - це рівняння, яке показує два еквівалентних співвідношення.
Співвідношення	Співвідношення - це порівняння двох величин, які можуть бути записані у вигляді дробу, з двокрапкою або зі словом «до».
Коефіцієнт масштабування	Масштабний коефіцієнт - це відношення масштабу до вихідного або фактичного виміру, написаного в найпростішій формі.
Трапеція	Трапеція - це чотирикутник з рівно однією парою паралельних протилежних сторін.

Додаткові ресурси

Інтерактивний елемент

Відео: Принципи площі та периметра аналогічних полігонів - Основні

Діяльність: Площа та периметр подібних полігонів Питання обговорення

Навчальні посібники: Посібник з вивчення периметра та області

Реальний світ: У ляльковому будинку