5.21: Площа регулярних і нерегулярних багатокутників
- Page ID
- 54767
Половина апофему разів на периметр.
Площа правильних багатокутників
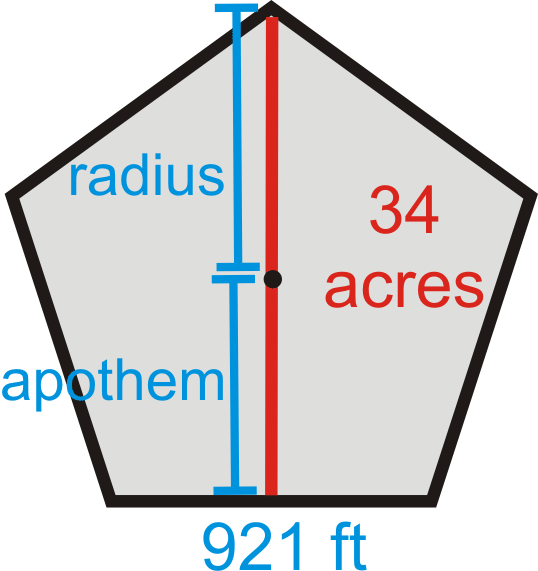
Що робити, якщо вас попросили знайти відстань через Пентагон в Арлінгтоні, штат Віргінія? Пентагон, в якому також знаходиться Міністерство оборони, складається з двох звичайних п'ятикутників з однаковим центром. Вся площа будівлі становить 29 акрів (40,000 квадратних футів в акрі), з додатковим двором 5 акрів в центрі. Довжина кожної зовнішньої стіни становить 921 фут. Яка загальна відстань через п'ятикутник? Округлите свою відповідь до найближчої сотої.

Правильний багатокутник - це багатокутник з конгруентними сторонами і кутами. Нагадаємо, що периметр квадрата в 4 рази перевищує довжину сторони, оскільки кожна сторона є конгруентною. Ми можемо розширити цю концепцію до будь-якого регулярного багатокутника.
Периметр регулярного багатокутника: Якщо довжина сторони дорівнює s, а в правильному багатокутнику є\(n\) сторони, то периметр дорівнює\(P=ns\).
Для того, щоб знайти площу правильного багатокутника, нам потрібно визначити нову термінологію. По-перше, всі правильні багатокутники можуть бути вписані в коло. Отже, правильні багатокутники мають центр і радіус, які є центром і радіусом описуваної окружності. Також як і коло, правильний багатокутник матиме утворений центральний кут. Однак у правильному багатокутнику центральний кут - це кут, утворений двома радіусами, притягнутими до послідовних вершин багатокутника. На малюнку нижче центральний кут -\(\angle BAD\). Також зверніть увагу, що\(\Delta BAD\) це рівнобедрений трикутник. Кожен правильний багатокутник з n сторонами утворений n рівнобедреними трикутниками. Висота цих рівнобедрених трикутників називається апофемом.
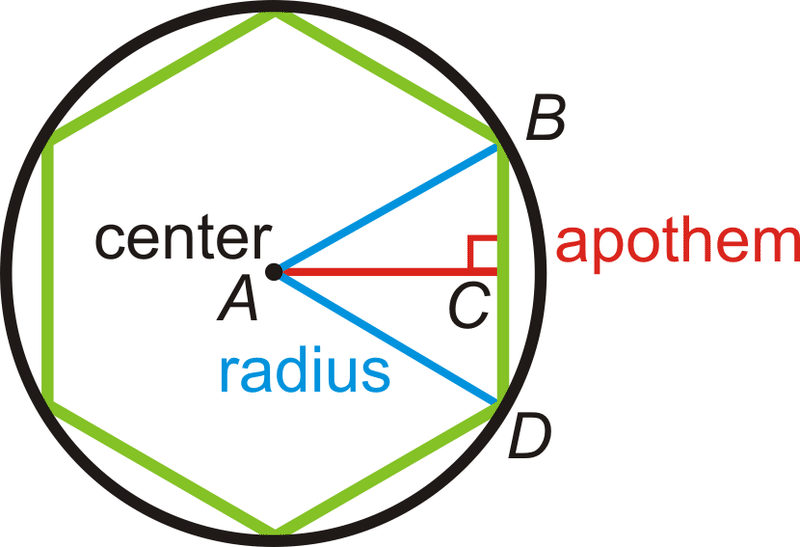
Площа кожного трикутника дорівнює\(A_{\Delta} =\dfrac{1}{2}bh=\dfrac{1}{2}sa\), де s - довжина сторони, а a - апотема. Якщо в правильному багатокутнику є n сторін, то він складається з n конгруентних трикутників.
Площа регулярного багатокутника: Якщо у правильному багатокутнику є n сторін довжиною s, а a - апотема, то\(A=\dfrac{1}{2}asn\) or\(A=\dfrac{1}{2}aP\), де\(P\) - периметр.
Обчислення периметра
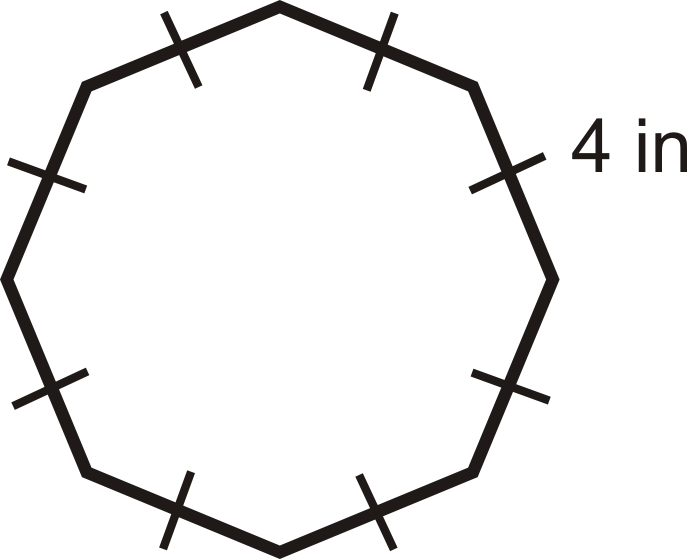
Який периметр правильного восьмикутника з 4-дюймовими сторонами?
Якщо кожна сторона 4 дюйми і є 8 сторін, це означає, що периметр є\(8(4\text{ in }) = 32\text{ inches }\).
Пошук довжини сторін
Периметр правильного гептагону - 35 см. Яка довжина кожної сторони?
Якщо\(P=ns\), то\(35\text{ cm }=7s\). Тому,\(s=5\text{ cm }\).
Пошук довжини апофему
Знайдіть довжину апофему в правильному восьмикутнику. Округлите свою відповідь до найближчої сотої.
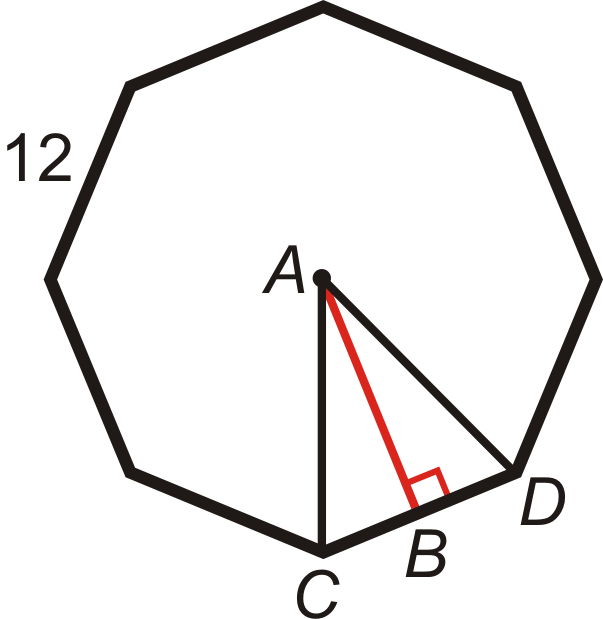
Щоб знайти довжину апофема, AB, потрібно буде використовувати коефіцієнти трига. Спочатку знайдіть\(m\angle CAD\). Є\(360^{\circ}\) навколо точки, так що\(m\angle CAD=\dfrac{360^{\circ}}{8}=45^{\circ}\). Тепер ми можемо використовувати це, щоб знайти інші два кути в\(\Delta CAD\). m\ кут ACB\) і m\ кут АЦП\) рівні, тому що\ Delta CAD\) є прямокутним трикутником.
\(\begin{aligned}m\angle CAD+m\angle ACB+m\angle ADC&=180^{\circ} \\ 45^{\circ}+2m\angle ACB&=180^{\circ} \\ 2m\angle ACB&=135^{\circ} \\ m\angle ACB&=67.5^{\circ}\end{aligned}\)
Щоб знайти AB, ми повинні використовувати тангенс співвідношення. Можна використовувати або гострий кут.
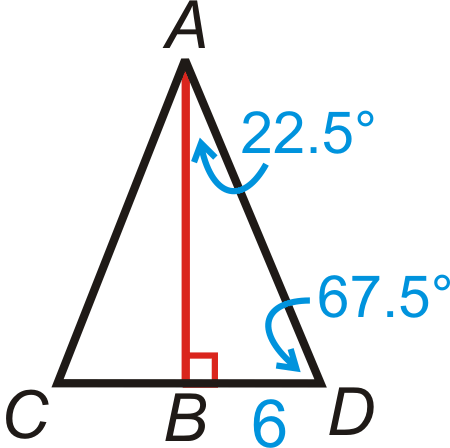
\(\begin{aligned}tan67.5^{\circ}&=\dfrac{AB}{6} \\ AB&=6\cdot tan67.5^{\circ}\approx 14.49\end{aligned}\)
Повторно переглянута проблема Пентагону
З малюнка нижче ми бачимо, що загальна відстань через Пентагон - це довжина апофема плюс довжина радіуса. Якщо загальна площа Пентагону становить 34 акрів, це 2,720,000 квадратних футів. Тому рівняння площі є,\(2720000=\dfrac{1}{2}a(921)(5)\) а апотема становить 590,66 футів. Щоб знайти радіус, ми можемо або використовувати теорему Піфагора, з апофемом і половиною довжини сторони або синусоїдальним співвідношенням. Нагадаємо, з Прикладу 5, що кожен центральний кут у п'ятикутнику\(72^{\circ}\), тому ми б використали половину цього для прямокутного трикутника.
\(sin36^{\circ}=\dfrac{460.5}{r} \rightarrow r=\dfrac{460.5}{sin36^{\circ}}\approx 783.45\text{ ft }\)
Тому загальна відстань поперек дорівнює\(590.66+783.45=1374.11\: ft\).
Приклад\(\PageIndex{1}\)
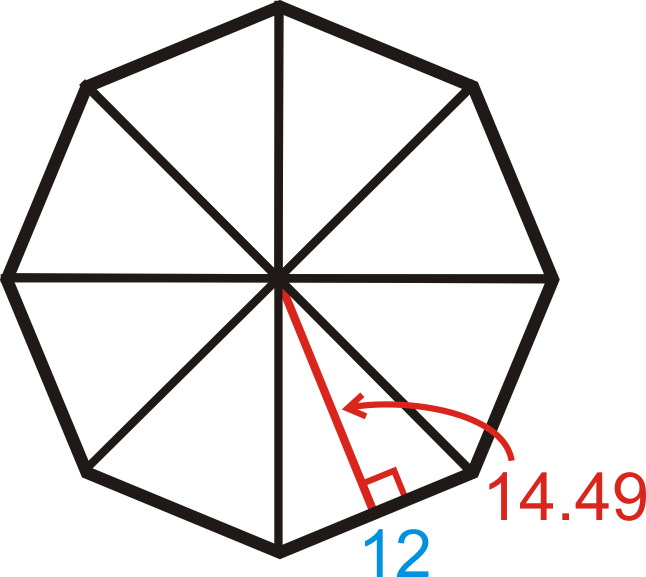
Знайдіть площу правильного восьмикутника в прикладі C.
Рішення
Восьмикутник можна розділити на 8 конгруентних трикутників. Отже, якщо ми знайдемо площу одного трикутника і помножимо її на 8, у нас вийде площа всього восьмикутника.
\(A_{octagon}=8(12\cdot 12\cdot 14.49)=695.52 units^2\)
Приклад\(\PageIndex{2}\)
Знайти площу правильного багатокутника з радіусом 4.
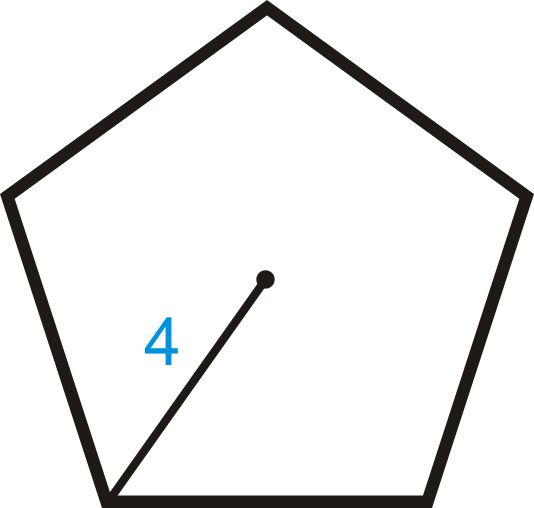
Рішення
INSERTB У цій задачі нам потрібно знайти апофем і довжину сторони, перш ніж ми зможемо знайти площу всього багатокутника. Кожен центральний кут для звичайного п'ятикутника є\(\dfrac{360^{\circ}}{5}=72^{\circ}\). Отже, половина того, щоб зробити прямокутний трикутник з апофемом, є\(36^{\circ}\). Нам потрібно використовувати синус і косинус.
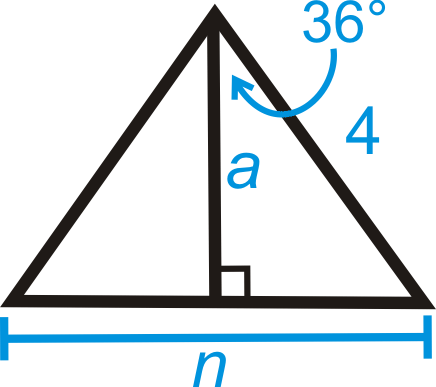
\ (\ почати {масив} {rlr}
\ sin 36^ {\ circ} & =\ розрив {.5 n} {4} &\ cos 36^ {\ circ} &=\ гідророзриву {a} {4}\\
4\ sin 36^ {\ circ} & =\ гідророзриву {1} {2} n & 4\ cos 36^ {\ circ} &=a\
8\ sin 36^ {\ circ} & = n & a\ приблизно 3,24\\
n &\ приблизно 4.7
\ end {масив}\)
Використовуючи ці дві частини інформації, ми тепер можемо знайти область. \(A=12(3.24)(5)(4.7)\approx 38.07 units^2\).
Приклад\(\PageIndex{3}\)
Площа правильного шестикутника дорівнює,\(54\sqrt{3}\) а периметр - 36. Знайдіть довжину сторін і апотема.
Рішення
Підключіть те, що ви знаєте, як до формул площі, так і периметра, щоб вирішити довжину сторони та апотема.
\ (\ почати {масив} {rlrl}
P & = S n & A & =\ розрив {1} {2} а Р\\
36&= 6 с & 54\ sqrt {3} & =\ frac {1} {2} a (36)\\
s&=6 & 54\ sqrt {3} & =18 a\
3\ sqrt {3} &=a
\ кінець масив}\)
Рецензія
Використовуйте правильний шестикутник нижче, щоб відповісти на наступні питання. Кожна сторона довжиною 10 см.
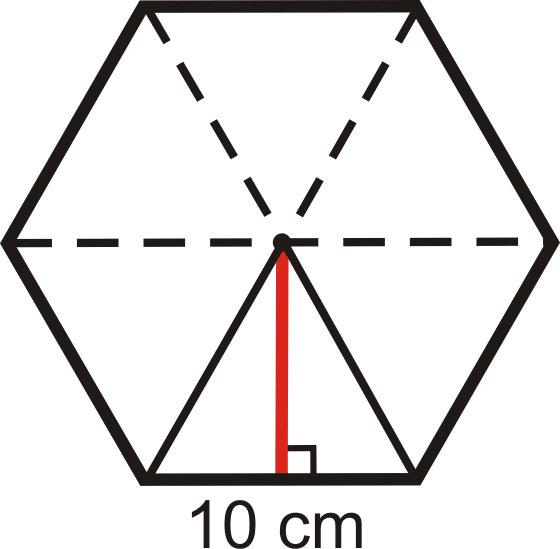
- Кожен пунктирний відрізок лінії - a (n) ________________.
- Червоний відрізок лінії - a (n) __________________.
- У правильному шестикутнику є _____ конгруентні трикутники.
- У правильному шестикутнику все трикутники _________________.
- Знайдіть радіус цього шестикутника.
- Знайдіть апофем.
- Знайдіть периметр.
- Знайдіть місцевість.
Знайдіть площу та периметр кожного з наступних правильних багатокутників. Округлите свою відповідь до найближчої сотої.
-
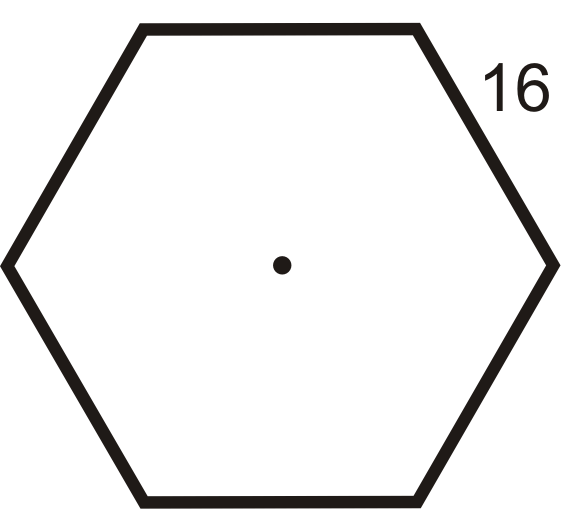
Малюнок\(\PageIndex{11}\) -
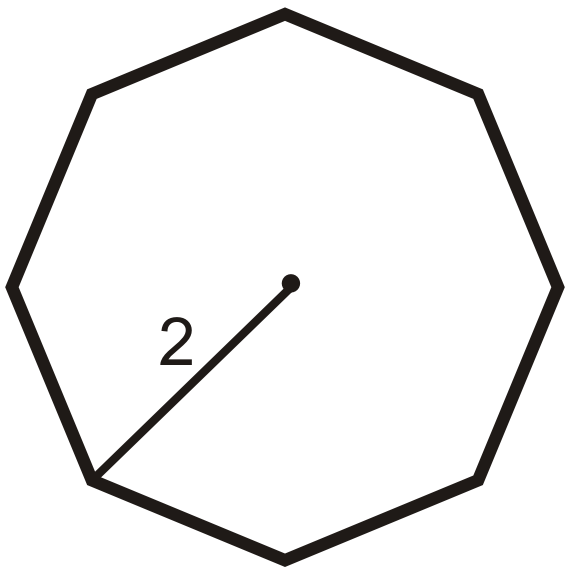
Малюнок\(\PageIndex{12}\) -
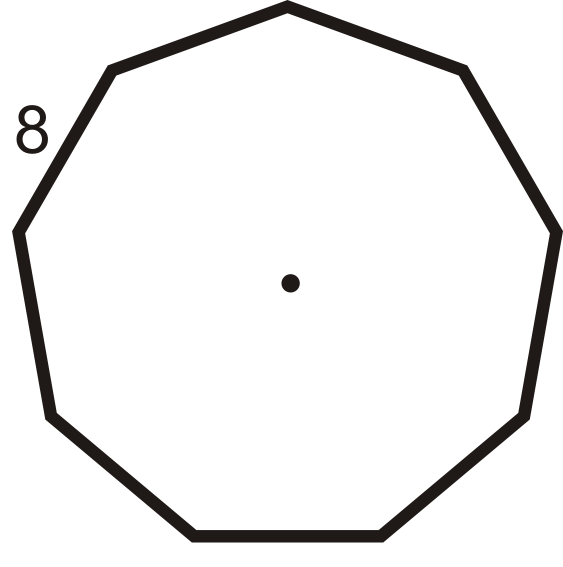
Малюнок\(\PageIndex{13}\) -
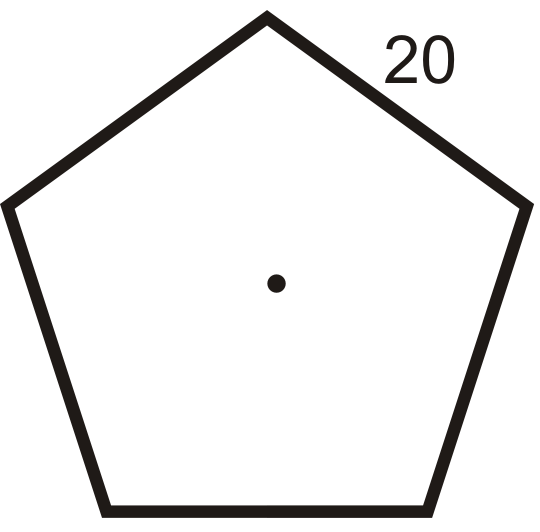
Малюнок\(\PageIndex{14}\) - Якщо периметр правильного декагона дорівнює 65, яка довжина кожної сторони?
- Правильний багатокутник має периметр 132, а сторони - 11 одиниць довжини. Скільки сторін має багатокутник?
- Площа правильного п'ятикутника становить,\(440.44\text{ in }^2\) а периметр - 80 дюймів. Знайдіть довжину апофему п'ятикутника.
- Площа правильного восьмикутника становить,\(695.3\text{ cm }^2\) а сторони - 12 см. Яка довжина апофему?
Правильний 20-кутник і правильний 40-кутник вписані в коло радіусом 15 одиниць.
- Виклик Вивести формулу для площі правильного шестикутника зі сторонами довжини s. Вашою єдиною змінною буде s. Підказка: Використовуйте співвідношення трикутників 30-60-90.
- Виклик на наступних кроках ви отримаєте альтернативну формулу для знаходження площі правильного багатокутника з n сторін.
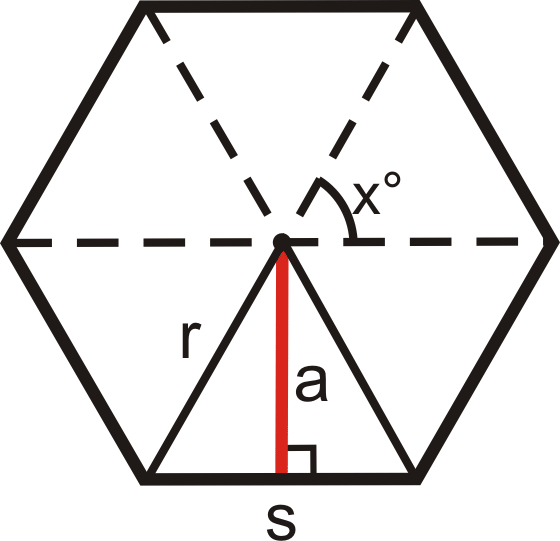
Ми збираємося почати з мислення багатокутника з n сторін як n конгруентних рівнобедрених трикутників. Суму площ цих трикутників ми знайдемо за допомогою тригонометрії. По-перше, площа трикутника дорівнює\(\dfrac{1}{2}bh\). На діаграмі праворуч ця формула області буде\(\dfrac{1}{2}sa\), де s - довжина сторони, а a - довжина апофему. На схемі\(x\) представлена міра кута вершини кожного рівнобедреного трикутника.
- Апофем, a, ділить трикутник на два конгруентних прямокутних трикутника. Верхній кут у кожного є\(\dfrac{x^{\circ}}{2}\). Знайти\(sin(\dfrac{x^{\circ}}{2})\) і\(cos(\dfrac{x^{\circ}}{2})\).
- Вирішіть своє рівняння гріха, щоб знайти вираз для s з точки зору\(r\) і\(x\).
- Вирішіть своє рівняння cos, щоб знайти вираз для a з точки зору\(r\) і\(x\).
- Підставляємо ці вирази в рівняння для площі одного з трикутників,\ dfrac {1} {2} sa\).
- Оскільки в n-кутнику буде n трикутників, вам потрібно помножити ваш вираз з частини d на n, щоб отримати загальну площу.
- Як би ви сказали комусь знайти значення\(x\) для регулярного n-кутника?
Використовуйте формулу, отриману в задачі 18, щоб знайти площу правильних багатокутників, описаних у задачах 19-22. Округляйте свої відповіді до найближчих сотих.
- Декагон радіусом 12 см.
- 20-кутник з радіусом 5 дюймів.
- 15-кутник з радіусом довжини 8 см.
- 45-кутник з радіусом довжини 7 дюймів.
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 10.12.
Додаткові ресурси
Інтерактивний елемент
Відео: Принципи площі правильних багатокутників
Практика: Площа регулярних і нерегулярних багатокутників