Skip to main content
LibreTexts - Ukrayinska

5.20: Регулярні та нерегулярні багатокутники

  1. Last updated
  2. Save as PDF
  • Page ID
    54860

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Зрозумійте та визначте правильні та нерегулярні багатокутники.

    F-D_8404B2EF9A86D62148369795924b3B99F9CBCC77E985B07a49c75809+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_jpg
    Малюнок\(\PageIndex{1}\)

    Логан простежував вуличні знаки по всьому своєму місту. Він готується простежити вищевказаний вуличний знак. Він окреслює форму, і він малює круглі краї у вигляді прямих ліній. Чи отримана форма буде правильним або неправильним багатокутником, і який тип багатокутника це буде?

    У цій концепції ви дізнаєтеся, як визначити, чи є багатокутник правильним або нерегулярним.

    Визначення, чи є полігони регулярними чи нерегулярними

    Багатокутник може мати певну кількість сторін, але сторони не обов'язково повинні бути однакової довжини. Обидва полігони нижче - це п'ятикутники, оскільки вони обидва мають п'ять кутів і сторін, але подивіться на відмінності.

    F-D_875EB ліжко 1E5B3D6824083 197950089487Е1 ААФ 79182D4A6DC5E4F06B+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    У першому п'ятикутнику всі кути конгруентні, а всі сторони - конгруентні. У другому п'ятикутнику кути мають різні міри, а сторони мають різну довжину.

    Правильний багатокутник має конгруентні кути і конгруентні сторони . Будь-який багатокутник може бути правильним багатокутником.

    Подивіться на правильні багатокутники нижче.

    F-д_Д843798С3879А36Б39С1Д826277ЕД 6185385Ф70Д2398Б2ФА7336А259+зображення_крихіткий+зображення_крихіткий_PNG
    Малюнок\(\PageIndex{3}\)

    Як бачите, правильний шестикутник має шість конгруентних сторін і шість конгруентних кутів. Правильний шестикутник, незалежно від довжини його сторін, завжди матиме кути, які вимірюють\(120^{\circ}\).

    Правильний восьмикутник має вісім конгруентних кутів і вісім конгруентних сторін. Кожен звичайний восьмикутник має однакові кутові заходи.

    Термін «звичайний прямокутник» зазвичай не використовується, оскільки прямокутник із конгруентними сторонами насправді є квадратом. Чотири кути в квадраті завжди\(90^{\circ}\), і їх сума завжди\(360^{\circ}\). Однак існує спеціальна назва для «правильного трикутника». Трикутник з трьома конгруентними сторонами називається рівностороннім трикутником. Його три кути завжди\(60^{\circ}\), і їх сума завжди\(180^{\circ}\).

    Будь-який багатокутник, який не має всіх конгруентних сторін, є неправильним багатокутником . Нерегулярні багатокутники все ще можуть бути п'ятикутниками, шестикутниками та неагонами, але вони не мають конгруентних кутів або рівних сторін. Ось кілька прикладів нерегулярних багатокутників.

    F-д_431 дБ9491158Д597Б1А5А99173839А8С7Фаб3БФ 920373C9D3E5+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    У цих багатокутників деякі сторони явно довші за інші, а деякі кути ширші за інші, тому вони повинні бути нерегулярними. Зверніть увагу, що нерегулярні багатокутники, як правило, виглядають нерівними або однобокими, тоді як правильні багатокутники виглядають більш впорядкованими та симетричними.

    Давайте розглянемо приклад ідентифікації нерегулярних і правильних багатокутників.

    Визначте багатокутник нижче і скажіть, правильний він чи нерегулярний.

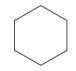
    F-D_C07C81CC854789ФФА902С2ФБ9836ФББ49378C7A73E9FA2F82A3E9D95+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_jpg
    Малюнок\(\PageIndex{5}\)

    Спочатку порахуйте кількість сторін.

    Форма має 6 сторін.

    Далі визначте, чи конгруентні сторони.

    Сторони конгруентні.

    Потім позначте багатокутник як правильний або нерегулярний.

    Регулярний.

    Відповідь полягає в тому, що багатокутник є правильним шестикутником.

    Коли лінії перетинаються в геометричній площині, вони утворюють багатокутники. Застосуйте те, що ви знаєте, щоб класифікувати ці багатокутники. Знайти довжини сторін, або вирішити для невідомих кутових заходів.

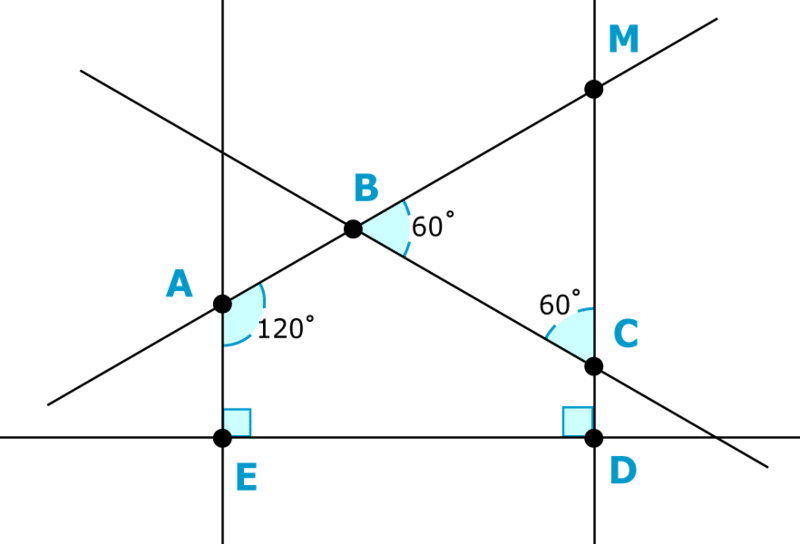
    F-д_098д078Ф47Ф614БА 3А9502А449 АЧ113940С356Ф5Б6Б677А44ФЕ3E2A+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    Перетин цих п'яти ліній створив кілька різних багатокутників. Для початку давайте їх ідентифікуємо.

    Найбільшим є\(AMDE\). У межах цієї цифри є дві цифри.

    Один - фігура\(ABCDE\). \(ABCDE\)має п'ять кутів і п'ять сторін, тому він є п'ятикутником. Два його кути вимірюють\(90^{\circ}\), а один\(120^{\circ} \) вимірює Що означає, що багатокутник - це нерегулярний п'ятикутник. Для того щоб знайти мірки двох інших кутів, потрібно поглянути на третю фігуру.

    Третя фігура - трикутник\(MBC\). Вона має два\(60^{\circ}\) кути. Кути\(ABC\) і\(MBC\) є додатковими. Іншими словами, разом вони утворюють пряму лінію. Вимірюється пряма лінія\(180^{\circ}\). Тому сума цих двох кутів дорівнює 180^ {\ circ}\). Просто відніміть, щоб знайти міру\(ABC\).

    \(180−60=120^{\circ}\)

    Кут ABC є\(120^{\circ}\).

    Тепер знайдемо міру кута\(BCD\). Тепер ви знаєте чотири з п'яти кутів на малюнку\(ABCDE\). Оскільки це п'ятикутник, ви також знаєте, що його внутрішні кути повинні мати суму\(540^{\circ}\). Ви можете налаштувати рівняння, щоб знайти міру невідомого кута.

    \(\begin{aligned} 90+90+120+120+\angle BCD&=540^{\circ} \\ 420+\angle BCD&=540^{\circ} \\ \angle BCD&=540−420 \\ \angle BCD&=120^{\circ} \end{aligned}\)

    П'ятий і кінцевий кут необхідно виміряти\(120^{\circ}\). Давайте складемо всі кути в п'ятикутник, щоб переконатися, що вони загальні\(540^{\circ}\).

    \(90+90+120+120+120=540^{\circ}\)

    Є ще один невідомий кут, кут AMD\). Існує два різних способи знайти міру третього кута в трикутнику\(BMD\). Ви знаєте, що три кути в трикутнику мають суму\(180^{\circ}\). Це також четвертий кут у чотирикутник\(AMDE\), і ви знаєте, що чотири кути в чотирикутник мають суму\(360^{\circ}\). Ви можете налаштувати рівняння для пошуку\(AMD\).

    \(\begin{aligned}60+60+\angle AMD&=180^{\circ} \\ 120+\angle AMD&=180^{\circ} \\ \angle AMD&=180−120 \\ \angle AMD&=60^{\circ}\end{aligned}\)

    Приклад\(\PageIndex{1}\)

    F-D_8404B2EF9A86D62148369795924b3B99F9CBCC77E985B07a49c75809+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_jpg
    Малюнок\(\PageIndex{7}\)

    Раніше вам дали проблему з приводу Логана і вищевказаного вуличного знака.

    Якщо він простежує форму знака, отримана форма буде правильним або неправильним багатокутником, і який тип багатокутника це буде?

    Рішення

    Спочатку порахуйте кількість сторін.

    Форма має 6 сторін.

    Далі визначте, чи конгруентні сторони.

    Сторони не конгруентні.

    Потім позначте багатокутник як правильний або нерегулярний.

    Нерегулярні.

    Відповідь полягає в тому, що багатокутник - це нерегулярний шестикутник.

    Приклад\(\PageIndex{2}\)

    Назвіть цю цифру.

    F-д_Ф 46 СЕ 054 СА9702ФА44Д1335 БК Ф 922578314 ЕФ756CE099EF3E164C6C+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{8}\)

    Рішення

    Спочатку порахуйте кількість сторін.

    Форма має 5 сторін.

    Далі визначте, чи конгруентні сторони.

    Сторони не конгруентні.

    Потім позначте багатокутник як правильний або нерегулярний.

    Нерегулярні.

    Відповідь - багатокутник - це нерегулярний п'ятикутник.

    Приклад\(\PageIndex{3}\)

    Назвіть цю цифру.

    F-D_5d92917a205c40FE1D0A806ef341de4851c63D60162059a26F59A26F597410+зображення_thumb_поштова листівка_крихітка+зображення_великий палецька_листівка_крихітка_jpg
    Малюнок\(\PageIndex{9}\)

    Рішення

    Спочатку порахуйте кількість сторін.

    Форма має 7 сторін.

    Далі визначте, чи конгруентні сторони.

    Сторони не конгруентні.

    Потім позначте багатокутник як правильний або нерегулярний.

    Нерегулярні.

    Відповідь полягає в тому, що багатокутник - це нерегулярний гептагон.

    Приклад\(\PageIndex{4}\)

    Класифікуйте фігуру як неправильну або правильну та визначте багатокутник.

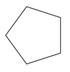
    F-D_E28215E05AB684C07AEAFD261648F0442AC0F310512568DE939332B+зображення_thumb_поштова листівка_крихітка+зображення_thumb_поштова листівка_крихітка_jpg
    Малюнок\(\PageIndex{10}\)

    Рішення

    Спочатку порахуйте кількість сторін.

    Форма має 5 сторін.

    Далі визначте, чи конгруентні сторони.

    Сторони здаються конгруентними.

    Потім позначте багатокутник як правильний або нерегулярний.

    Регулярний.

    Відповідь полягає в тому, що багатокутник - це правильний п'ятикутник.

    Приклад\(\PageIndex{5}\)

    Визначте багатокутник.

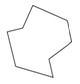
    F-D_067855F2052C73DB9CCFFC 196816FF23FD86810F4E478493F7DD2+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_jpg
    Малюнок\(\PageIndex{11}\)

    Рішення

    Спочатку порахуйте кількість сторін.

    Форма має 8 сторін.

    Далі визначте, чи конгруентні сторони.

    Сторони не конгруентні.

    Потім позначте багатокутник як правильний або нерегулярний.

    Нерегулярні.

    Відповідь полягає в тому, що багатокутник - це нерегулярний восьмикутник.

    Рецензія

    Визначте кожен чотирикутник за його описом.

    1. Чотирикутник з однією парою паралельних сторін.
    2. Чотирикутник з протилежними сторонами конгруентний і паралельний, з чотирма прямими кутами.
    3. Чотирикутник з чотирма конгруентними паралельними сторонами і чотирма прямими кутами.
    4. Прямокутник з чотирма конгруентними паралельними сторонами.

    Визначте багатокутники на схемі. Потім знайдіть мірки невідомих кутів.

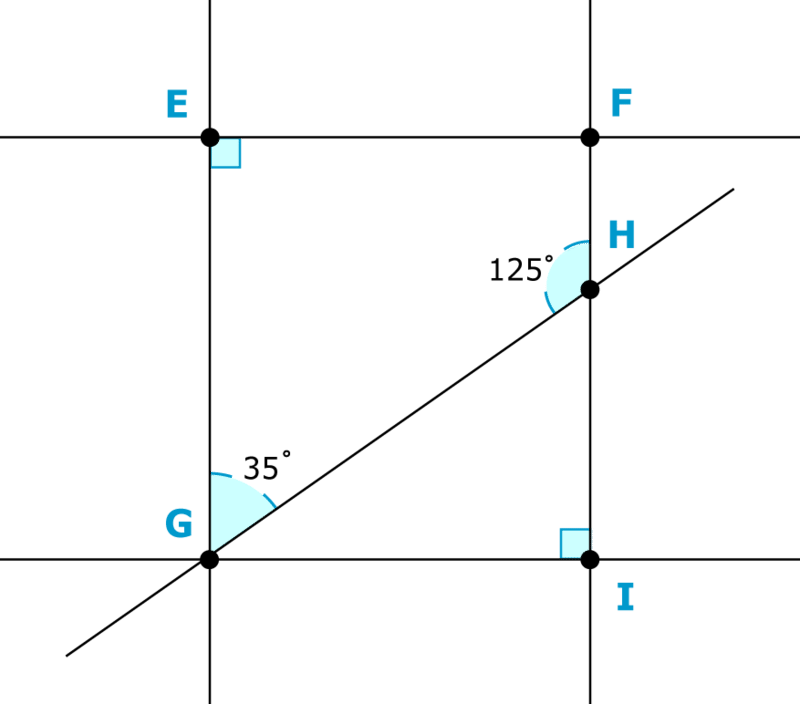
    1. F-D_3ЕФ2Д8БФ2ФД 8Е0Б8 Фе 6ББ Б 86174067c5266421E50F0E5A02C24615A+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)

    Відповідь true або false на кожне з наступних питань.

    1. Ромб - це завжди квадрат.
    2. Паралелограм має протилежні сторони, які паралельні.
    3. Прямокутник - це тип паралелограма.
    4. Квадрати, прямокутники і ромби - це паралелограми з чотирма прямими кутами.
    5. Трапеція має чотири прямих кута.
    6. Трапеція має одну пару паралельних сторін.
    7. Правильний багатокутник має конгруентні сторони та кути.
    8. П'ятикутник не може бути неправильним багатокутником.

    Визначте кожен багатокутник нижче.

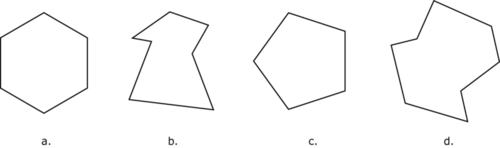
    F-D_96E54ECF35B69436FCE41E3F65DF12224C547C5932BDB5370A082D7+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{13}\)
    1. a
    2. б
    3. c
    4. d

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 8.11.

    Ресурси

    Лексика

    Термін Визначення
    Паралелограм Паралелограм - це чотирикутник з двома парами паралельних сторін.
    Багатокутник Багатокутник - це проста замкнута фігура з принаймні трьома прямими сторонами.
    Чотирикутник Чотирикутник - замкнута фігура з чотирма сторонами і чотирма вершинами.
    Прямокутник Прямокутник - це чотирикутник з чотирма прямими кутами.
    Ромб Ромб - це чотирикутник з чотирма конгруентними сторонами.
    Квадрат Квадрат - це багатокутник з чотирма конгруентними сторонами і чотирма прямими кутами.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Вступ до багатокутників

    Практика: Регулярні та нерегулярні багатокутники

    Реальний світ: Ідеальний Пентагон