5.19: Класифікація чотирикутників у координатній площині
- Page ID
- 54791
Визначте та обчислите площу фігур на основі координат на площині.
Класифікація чотирикутника
Що робити, якщо вам дали чотирикутник в координатній площині? Як ви могли визначити, чи цей чотирикутник кваліфікується як один із спеціальних чотирикутників: паралелограми, квадрати, прямокутники, ромби, повітряні змії чи трапеції?
Під час роботи в координатній площині іноді потрібно знати, який тип форми є заданою формою. Ви повинні легко мати можливість сказати, що це чотирикутник, якщо він має чотири сторони. Але як ви можете класифікувати його за межі цього?
Спочатку слід навести графік фігури, якщо вона ще не була графічна. Подивіться на нього і подивіться, чи схожий він на який-небудь спеціальний чотирикутник. Чи здаються сторони конгруентними? Зустрічаються вони під прямим кутом? Це дасть вам місце для початку.
Після того, як у вас є припущення для якого типу чотирикутника це, ваша робота полягає в тому, щоб довести свою здогадку. Щоб довести, що чотирикутник - це паралелограм, прямокутник, ромб, квадрат, повітряний змій або трапеція, ви повинні показати, що він відповідає визначенню цієї форми АБО що він має властивості, які має лише ця форма.
Якщо виявиться, що ваша здогадка виявилася неправильною через те, що форма не виконує необхідних властивостей, можна здогадатися ще раз. Якщо це, здається, немає типу спеціального чотирикутника, то це просто чотирикутник.
Наведені нижче приклади допоможуть вам побачити, як може виглядати цей процес.
Класифікація паралелограмів
Визначте, який тип паралелограма TUNE є:\(T(0,10),\: U(4,2),\: N(−2,−1),\: and\: E(−6,7)\).
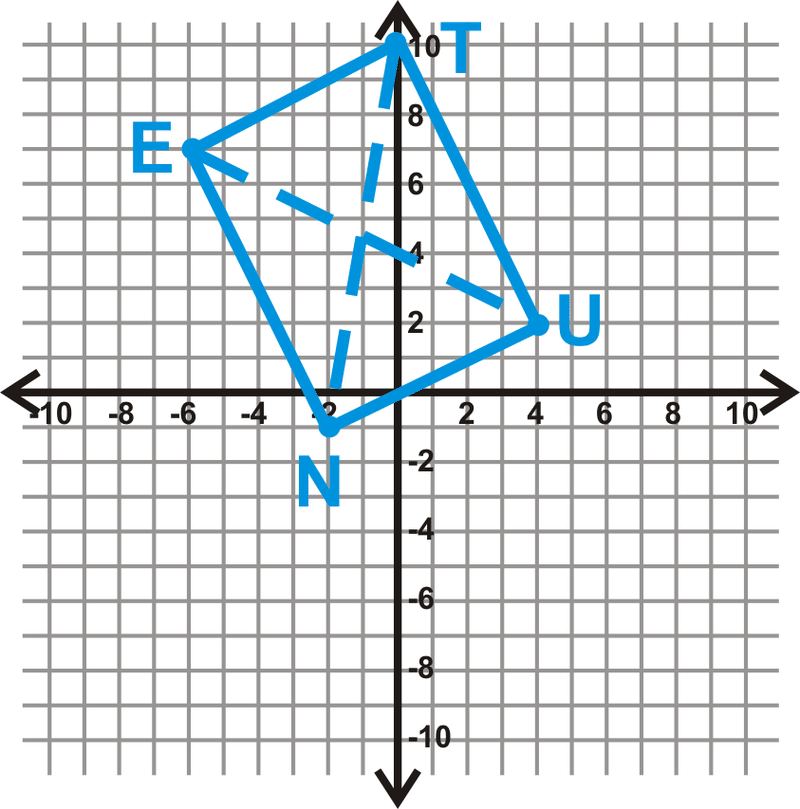
Це виглядає як прямокутник. Давайте подивимося, чи рівні діагоналі. Якщо вони є, то TUNE - це прямокутник.
\ (\ почати {вирівняний}
E U &=\ sqrt {(-6-4) ^ {2} + (7-2) ^ {2}} & T N &=\ sqrt {(0+2) ^ {2} + (10+1) ^ {2}}\\
&=\ sqrt {(-10) ^ {2} +5^ {2}} &=\ sqrt {(-10) ^ {2} +5^ {2}} &=\ sqrt {2} +11^ {2}}\\
&=\ sqrt {100+25} & =\ sqrt {4+121}\\
&=\ sqrt {125} & =\ sqrt {125}
\ end {вирівняний}\)
Якщо діагоналі також перпендикулярні, то\(TUNE\) це квадрат.
\(\text { Slope of } E U=\dfrac{7-2}{-6-4}=-\dfrac{5}{10}=-\dfrac{1}{2} \quad \text { Slope of } T N=\dfrac{10-(-1)}{0-(-2)}=\dfrac{11}{2}\)
Ухил\(EU\)\(\neq\) нахилу\(TN\),\(TUNE\) так виглядає прямокутник.
Визначення, чи чотирикутник є паралелограмом
Чотирикутник визначається чотирма лініями\(y=2x+1\),\(y=−x+5\),\(y=2x−4\), і\(y=−x−5\). Це чотирикутник паралелограм?
Щоб перевірити, чи є це паралелограм, ми повинні перевірити, чи є у нього дві пари паралельних сторін. З рівнянь видно, що нахили ліній складають 2, −1, 2 та −1. Оскільки дві пари схилів збігаються, ця форма має дві пари паралельних сторін і є паралелограмом.
Визначення типів чотирикутників
Визначте, який тип чотирикутника\(RSTV\) буває. Спрощення всіх радикалів.
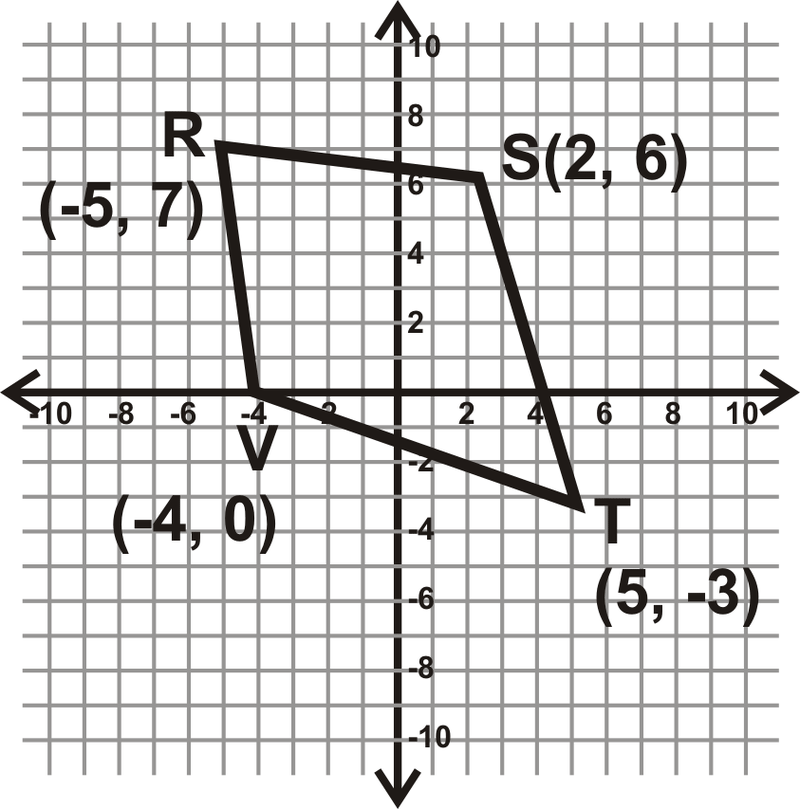
Є два напрямки, які ви могли б взяти тут. По-перше, ви могли б визначити, чи діагоналі перетинають один одного. Якщо вони роблять, то це паралелограм. Або ви можете знайти довжини всіх сторін. Давайте зробимо цей варіант.
\ (\ почати {вирівняний}
R S &=\ sqrt {(-5-2) ^ {2} + (7-6) ^ {2}} & S T &=\ sqrt {(2-5) ^ {2} + (6- (-3)) ^ {2}}\\
&=\ sqrt {(-7) ^ {2} +1^ {2}} &=\ sqrt {(-7) ^ {2} (-3) ^ {2} +9^ {2}}\\
&=\ sqrt {50} =5\ sqrt {2} & =\ sqrt {90} =3\ sqrt {10}\\
R V = &\ sqrt {(-5- (-4)) ^ {2} + (7-0) ^ {2}} & V T &=\ sqrt {(-4-5) ^ {2} + (0- (-3)) ^ {2}}\\
=&\ sqrt {(-1) ^ {2} +7^ {2}} & =\ sqrt {(-9) ^ {2} +3^ {2}\
=&\ sqrt {50} =5\ sqrt {2} & &=\ sqrt {90} =3\ sqrt {10}
\ кінець {вирівняний}\)
З цього ми бачимо, що сусідні сторони конгруентні. Тому\(RSTV\) є повітряний змій.
Інтерактивний елемент
Додайте тут інтерактивний текст елемента. Це поле НЕ буде друкувати в PDF-файлах
Огляд алгебри: Коли його просять «спростити радикал», витягніть усі квадратні числа (1, 4, 9, 16, 25,...) з радикала. Вище\(\sqrt{50}=\sqrt{25\cdot 2}\). Ми знаємо\(\sqrt{25}=5\), так\(\sqrt{50}=\sqrt{25\cdot 2}=5\sqrt{2}\).
Розпізнавання паралелограм
Чотирикутник\(ABCD\) є паралелограмом?
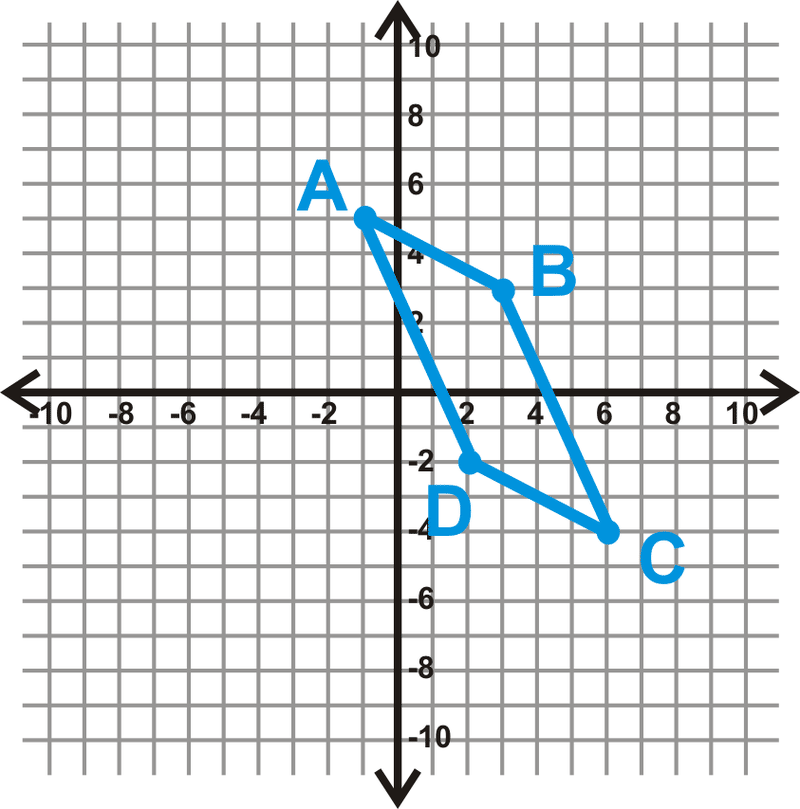
Ми визначили, що існує чотири різні способи показати чотирикутник - це паралелограм у\(x−y\) площині. Давайте перевіримо, чи є пара протилежних сторін конгруентна і паралельна. Спочатку знайдіть довжину\(AB\) і\(CD\).
\ (\ почати {вирівняний}
A B &=\ sqrt {(-1-3) ^ {2} + (5-3) ^ {2}} & C D &=\ sqrt {(2-6) ^ {2} + (-2+4) ^ {2}}\\
&=\ sqrt {(-4) ^ {2} +2^ {2}} &=\ sqrt {(-4) ^ {2} 2} +2^ {2}}\\
&=\ sqrt {16+4} & =\ sqrt {16+4}\\
&=\ sqrt {20} & =\ sqrt {20}
\ end {вирівняний}\)
\(AB=CD\), Так що якщо дві лінії мають однаковий нахил,\(ABCD\) це паралелограм.
\(\text { Slope } A B=\dfrac{5-3}{-1-3}=\dfrac{2}{-4}=-\dfrac{1}{2} \text { Slope } C D=\dfrac{-2+4}{2-6}=\dfrac{2}{-4}=-\dfrac{1}{2}\)
Тому\(ABCD\) є паралелограмом.
Приклад\(\PageIndex{1}\)
Чотирикутник визначається чотирма лініями\(y=2x+1\),\(y=−2x+5\),\(y=2x−4\), і\(y=−2x−5\). Чи є цей чотирикутник прямокутником?
Рішення
Щоб бути прямокутником, форма повинна мати чотири прямих кути. Це означає, що сторони повинні бути перпендикулярні один одному. З заданих рівнянь ми бачимо, що нахили складають 2, −2, 2 та −2. Оскільки схили не протилежні взаємно один одному, сторони не перпендикулярні, а форма не прямокутник.
Приклад\(\PageIndex{2}\)
Визначте, який тип чотирикутника\(ABCD\) буває. \(A(−3,3),\: B(1,5),\: C(4,−1),\: D(1,−5)\). Спрощення всіх радикалів.
Рішення
По-перше, графік\(ABCD\). Це дозволить легше розібратися, що це за тип чотирикутника. З графіка ми можемо сказати, що це не паралелограм. Знайдіть нахил\ overline {BC} та\ overline {AD}, щоб побачити, чи паралельні вони.
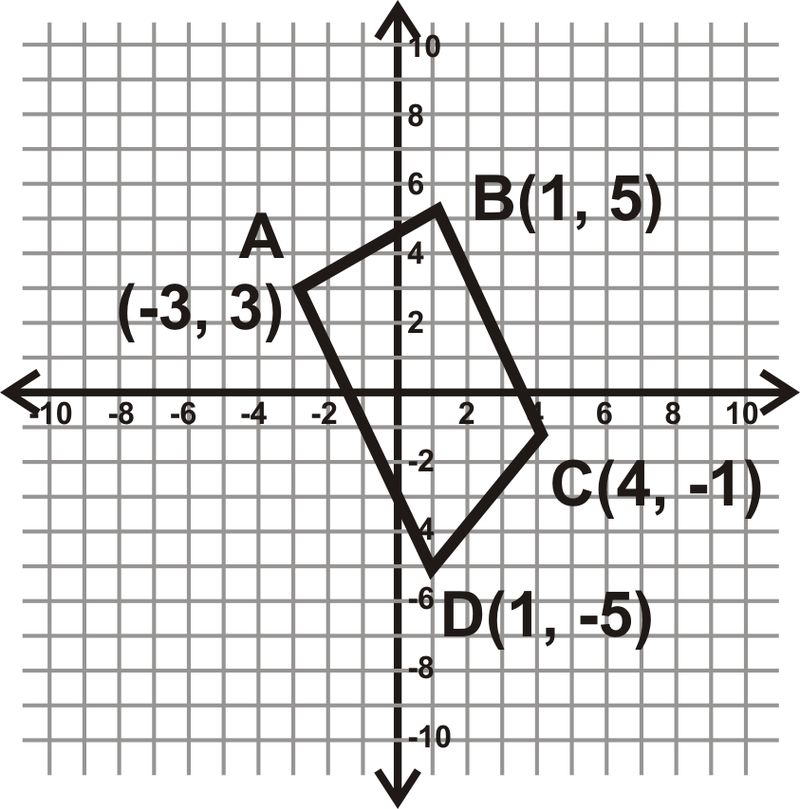
\ (\ begin {масив} {l}
\ текст {Нахил}\ оверлайн {B C} =\ dfrac {5- (-1)} {1-4} =\ dfrac {6} {-3} =
\ dfrac {3- (-5)} =\ dfrac {3- (-5)} {-3-1} =\ dfrac {8} {-4} =-2
\ end {масив}\)
Ми тепер знаємо\(\overline{BC} \parallel \overline{AD}\). Це трапеція. Щоб визначити, чи є це рівнобедреною трапецією, знайдіть\(AB\) і\(CD\).
\ (\ почати {вирівняний}
A B &=\ sqrt {(-3-1) ^ {2} + (3-5) ^ {2}} & S T &=\ sqrt {(4-1) ^ {2} + (-1- (-5)) ^ {2}}\\ &=\ sqrt {(-4) ^ {2} + (-2) ^ {2}}
&=\ sqrt {(-4) ^ {2} + (-2) ^ {2}} &=\ sqrt 3^ {2} +4^ {2}}\\
&=\ sqrt {20} =2\ sqrt {5} & =\ sqrt {25} =5
\ кінець {вирівняний}\)
\(AB\neq CD\), Тому це тільки трапеція.
Приклад\(\PageIndex{3}\)
Визначте, який тип чотирикутника\(EFGH\) буває. \(E(5,−1),\: F(11,−3),\: G(5,−5),\: H(−1,−3)\)
Рішення
Ми не будемо графувати цей приклад. Знайдемо довжину всіх чотирьох сторін.
\ (\ почати {вирівняний}
E F &=\ sqrt {(5-11) ^ {2} + (-1- (-3)) ^ {2}} & F G &=\ sqrt {(11-5) ^ {2} + (-3- (-5)) ^ {2}}\\
&=\ sqrt {(-6) ^ {2} +2^ {2}} &=\ sqrt {(-6) ^ {2} {6^ {2} +2^ {2}}\\
&=\ sqrt {40} =2\ sqrt {10} & =\ sqrt {40} =2\ sqrt {10}\\
G H &=\ sqrt { (5- (-1)) ^ {2} + (-5- (-3)) ^ {2}} & Н &=\ sqrt {(-1-5) ^ {2} + (-3- (-1)) ^ {2}}}\\
&=\ sqrt {6^ {2} + (-2) ^ {2}} & =\ sqrt {(-6) ^ {2} + (-2) ^ {2}} & =\ sqrt {(-6) ^ {2} + (-2)) ^ {2}}\\
=&\ sqrt {40} =2\ sqrt {10} & &=\ sqrt {40} =2\ sqrt {10}
\ кінець {вирівняний}\)
Всі чотири сторони рівні. Це означає, що цей чотирикутник або ромб, або квадрат. Різниця між ними полягає в тому, що квадрат має чотири кути 90і конгруентні діагоналі. Знайдемо довжину діагоналей.
\ (\ почати {вирівняний}
E G &=\ sqrt {(5-5) ^ {2} + (-1- (-5)) ^ {2}} & F H &=\ sqrt {(11- (-1)) ^ {2} + (-3- (-3)) ^ {2}}\\ &=\ sqrt {0^ {2} +4^ {2}}
&=\ sqrt {0^ {2} +4^ {2}} &=\ sqrt rt {12^ {2} +0^ {2}}\\
&=\ sqrt {16} =4 & =\ sqrt {144} =12
\ кінець {вирівняний}\)
Діагоналі не конгруентні, так\(EFGH\) це ромб.
Рецензія
- Якщо чотирикутник має рівно одну пару паралельних сторін, який це тип чотирикутника?
- Якщо чотирикутник має дві пари паралельних сторін і один прямий кут, який це тип чотирикутника?
- Якщо чотирикутник має перпендикулярні діагоналі, який це тип чотирикутника?
- Якщо чотирикутник має діагоналі, які перпендикулярні та конгруентні, який це тип чотирикутника?
- Якщо чотирикутник має чотири конгруентні сторони і один прямий кут, який це тип чотирикутника?
Визначте, який тип чотирикутника\(ABCD\) буває.
- \(A(−2,4),\: B(−1,2),\: C(−3,1),\: D(−4,3)\)
- \(A(−2,3),\: B(3,4),\: C(2,−1),\: D(−3,−2)\)
- \(A(1,−1),\: B(7,1),\: C(8,−2),\: D(2,−4)\)
- \(A(10,4),\: B(8,−2),\: C(2,2),\: D(4,8)\)
- \(A(0,0),\: B(5,0),\: C(0,4),\: D(5,4)\)
- \(A(−1,0),\: B(0,1),\: C(1,0),\: D(0,−1)\)
- \(A(2,0),\: B(3,5),\: C(5,0),\: D(6,5)\)
СРЮ - прямокутник, а PRUC - квадрат.
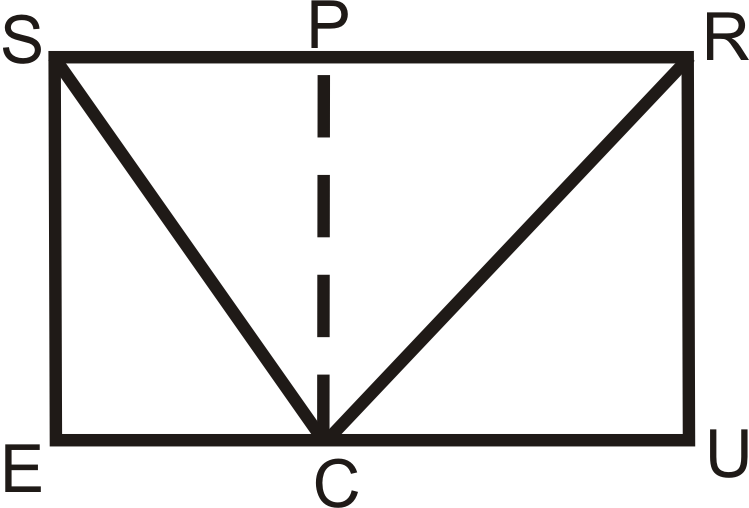
- Який тип чотирикутника буває\(SPCE\)?
- Якщо\(SR=20\) і\(RU=12\), знайдіть\(CE\).
- Знайдіть СК і РЦ на основі інформації з частини б. округляйте свої відповіді до найближчих сотих.
Огляд (Відповіді)
Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 6.8.
Лексика
| Термін | Визначення |
|---|---|
| Повітряний змій | Повітряний змій - це чотирикутник з чітко вираженими суміжними конгруентними сторонами. |
| Паралелограм | Паралелограм - це чотирикутник з двома парами паралельних сторін. |
| Чотирикутник | Чотирикутник - замкнута фігура з чотирма сторонами і чотирма вершинами. |
| Прямокутник | Прямокутник - це чотирикутник з чотирма прямими кутами. |
| Ромб | Ромб - це чотирикутник з чотирма конгруентними сторонами. |
| Трапеція | Трапеція - це чотирикутник з рівно однією парою паралельних протилежних сторін. |