5.18: Площа та периметр композитних фігур

Last updated
Save as PDF

Page ID: 54818

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Знайдіть площу та периметр фігур, що складаються з двох або більше поширених фігур.

Площа композитних фігур

Периметр - це відстань навколо фігури. Периметр будь-якої фігури повинен мати прикріплену до нього одиницю виміру. Якщо конкретних одиниць не вказано (фути, дюйми, сантиметри тощо), напишіть «одиниці».

Площа - це кількість простору всередині фігури. Якщо дві фігури конгруентні, вони мають однакову площу (Постулат конгруентних областей).

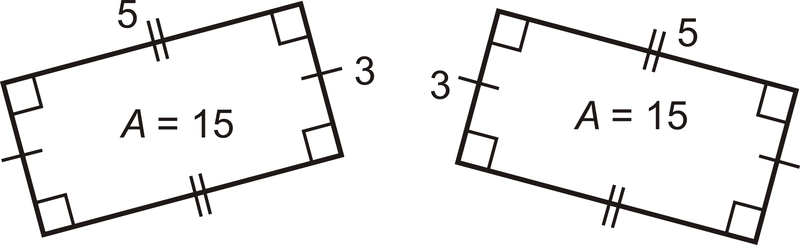
F-D_4103F74F847C617ФДД 3СА111Б42АА884Ф5923АД 74Е8 CFDF60CC88+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{1}\)

Композитна форма - це форма, що складається з інших фігур. Щоб знайти площу такої форми, просто знайдіть площу кожної деталі і складіть їх.

Постулат додавання площі: Якщо фігура складається з двох або більше частин, які не перекривають один одного, то площа фігури - це сума площ частин.

Розглянемо основний будинок, намальований у вигляді трикутника на вершині квадрата. Як ви могли знайти площу цієї складеної форми?

Приклад\(\PageIndex{1}\)

Знайдіть площу малюнка нижче. Всі кути, які виглядають як прямі кути, є прямими кутами.

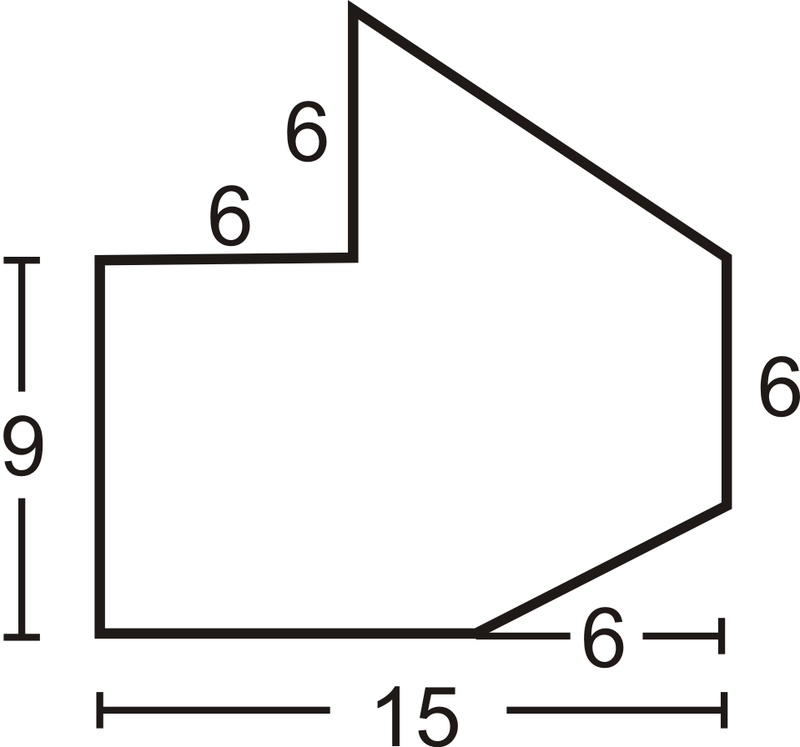
F-д_1Ф1795886 АФБА0951483579С32ЕДФ 05Ф837 АБД 587АБ 546CB3B+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

Рішення

Розділіть фігуру на трикутник і прямокутник з невеликим прямокутником виріжте з нижнього правого кута.

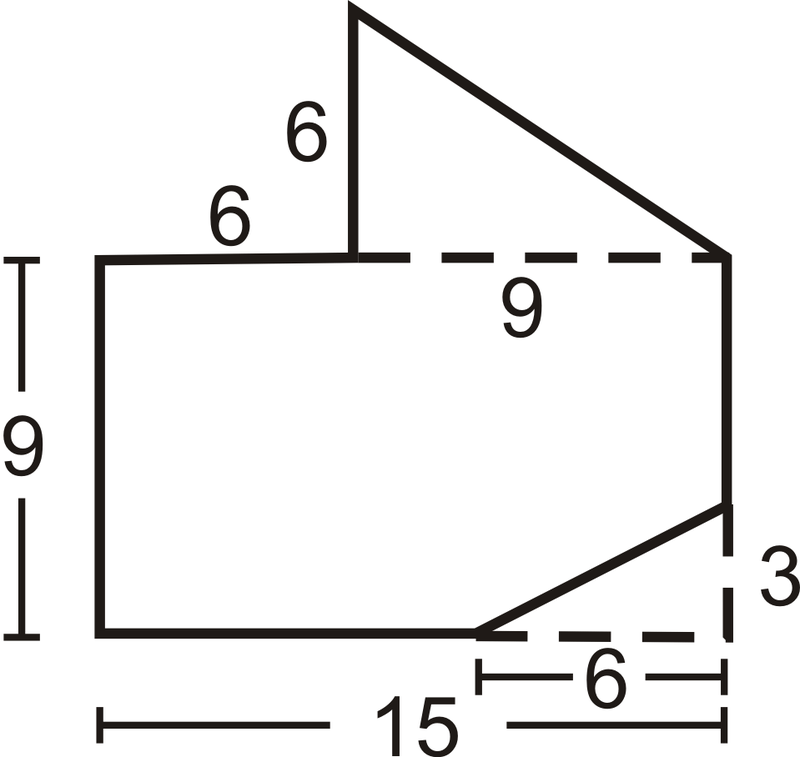
F-D_3BCFB82613D3EF4D5B567DAE818E27 АДС4263Ф3Ф3408571Д9Б769Е1Б70+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{3}\)

\(A=A_{\text{top triangle}}+A_{\text{rectangle}}−A_{\text{small triangle}} \\ A=(\dfrac{1}{2} \cdot 6\cdot 9)+(9\cdot 15))−(\dfrac{1}{2}\cdot 3\cdot 6) \\ A&=27+135−9 \\ A&=153\text{ units}^2\)

Приклад\(\PageIndex{2}\)

Розділіть форму на два прямокутника і один трикутник. Знайдіть площу двох прямокутників і трикутника. Всі кути, які виглядають як прямі кути, є прямими кутами.

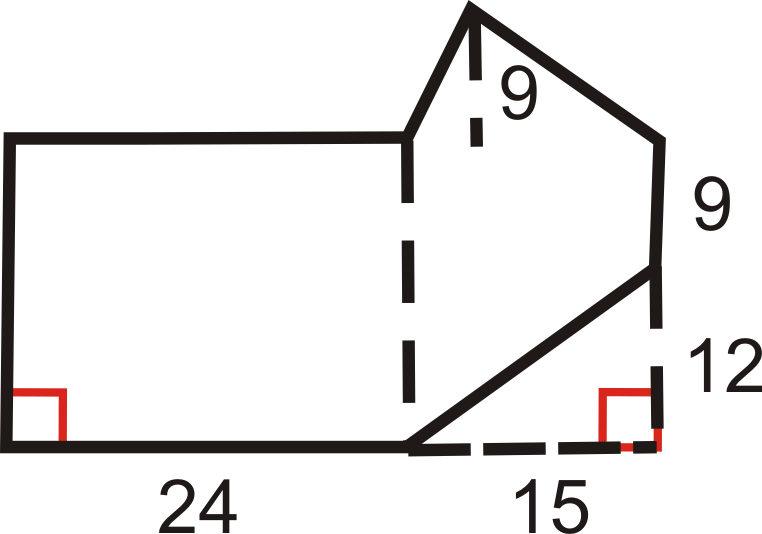
Ф-д_а79д 378075956Д908990БФ 9ФБ43237 КС3Е2ФББФ АЕ24C315606846+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{4}\)

Рішення

Прямокутник #1:\(\text{Area} =24(9+12)=504\text{ units}^2\)

Прямокутник #2:\(\text{Area}=15(9+12)=315\text{ units}^2\)

Трикутник:\(\text{Area} =15(9)2=67.5\text{ units}^2\)

Приклад\(\PageIndex{3}\)

Знайдіть площу всієї фігури з Прикладу 2 (потрібно буде відняти площу маленького трикутника в правому нижньому кутку).

Рішення

\(\text{Total Area} =504+315+67.5−\dfrac{15(12)}{2}=796.5 \text{ units}^2\)

Приклад\(\PageIndex{4}\)

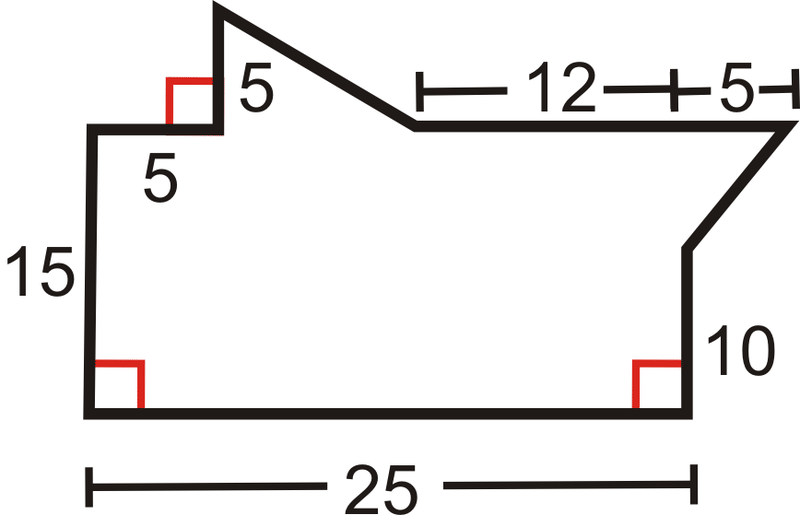
Ф-д_5ФКК9Е2БФ4ААА5А3С0Д21ДБ97Б ФК ФК3Б0Ф000Б1 Каб 94Ф3Ф4Д4Д4Д8+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{5}\)

Всі кути, які виглядають як прямі кути, є прямими кутами.

Розділіть фігуру на два трикутника і один прямокутник.
Знайдіть площу двох трикутників і прямокутника.
Знайдіть площу всієї фігури.

Рішення

Один трикутник зверху і один праворуч, решта фігури - прямокутник.
Площа трикутника зверху дорівнює\(\dfrac{8(5)}{2}=20\text{ units}^2\). Площа трикутника праворуч дорівнює\(\dfrac{5(5)}{2}=12.5\text{ units}^2\). Площа прямокутника дорівнює\(375\text{ units}^2\).
Загальна площа становить\(407.5\text{ units}^2\).

Рецензія

Використовуйте картинку нижче для питань 1-4. Композитна форма формується з квадрата всередині квадрата.

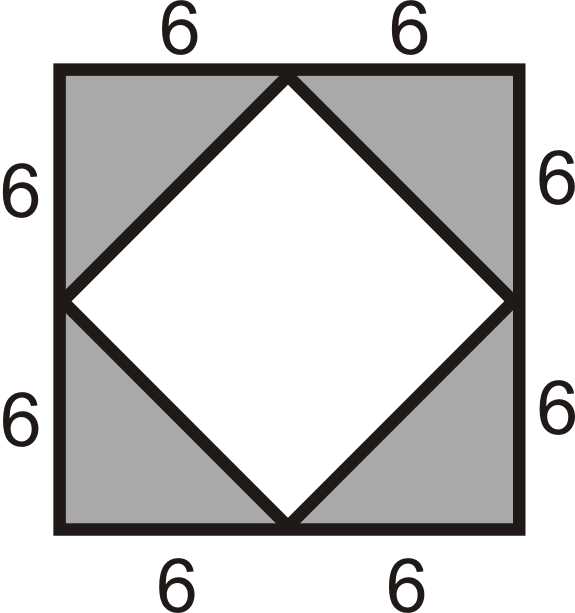
F-D_9593292257Ф4 ФА65Б53АЕ 9CDF1261 ФББД00БФБ3Б 1Д7ДД7Б32С597979+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{6}\)

Знайдіть площу зовнішнього квадрата.
Знайдіть площу одного сірого трикутника.
Знайдіть площу всіх чотирьох сірих трикутників.
Знайдіть площу внутрішнього квадрата.

Знайдіть області на малюнках нижче. Ви можете припустити, що всі сторони перпендикулярні.

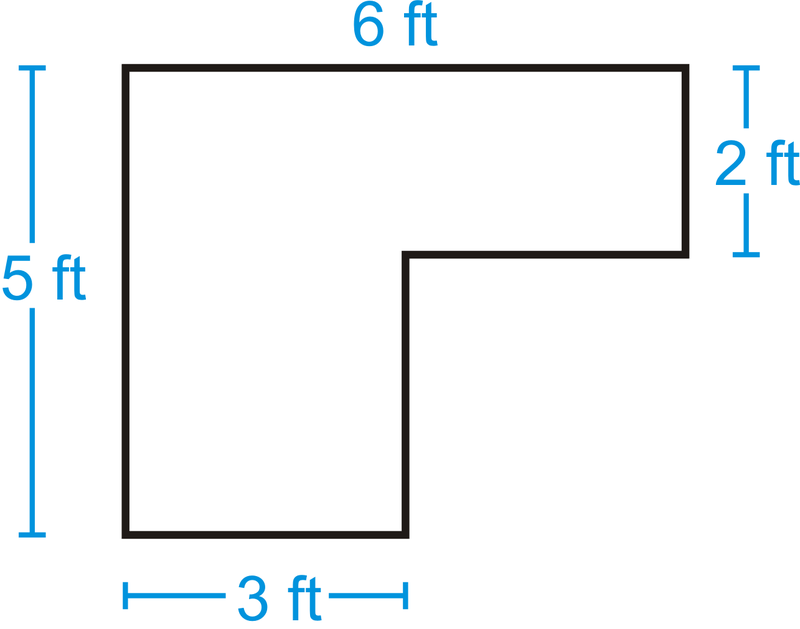
Малюнок\(\PageIndex{7}\)
Малюнок\(\PageIndex{8}\)

Знайдіть площі складових фігур.

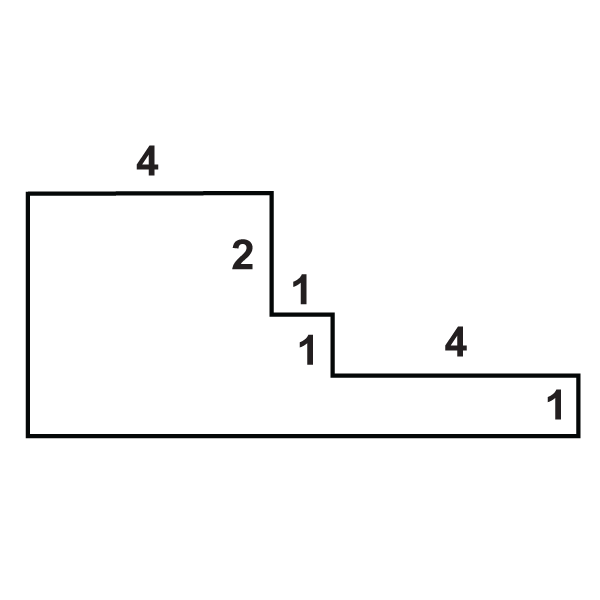
Малюнок\(\PageIndex{9}\)
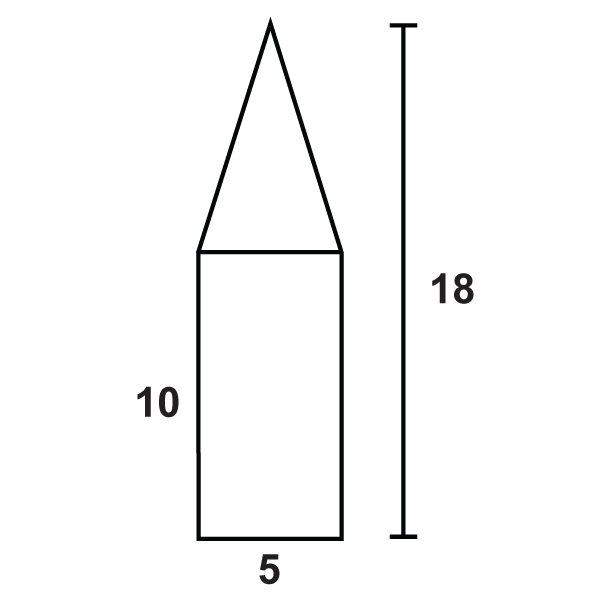
Малюнок\(\PageIndex{10}\)
Малюнок\(\PageIndex{11}\)
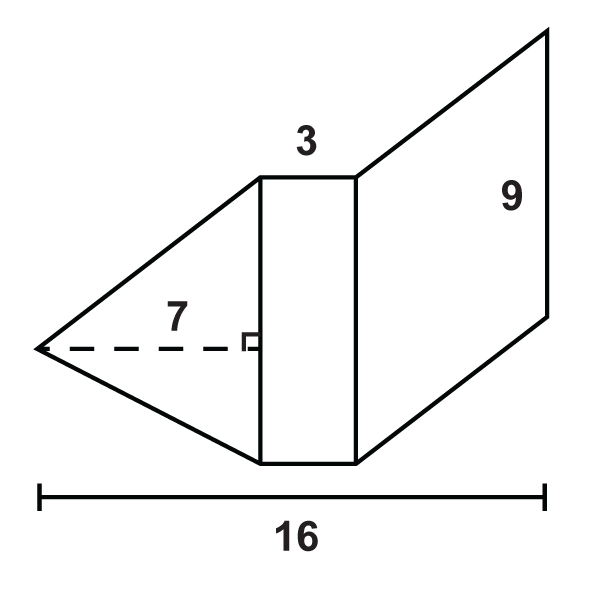
Малюнок\(\PageIndex{12}\)
Малюнок\(\PageIndex{13}\)
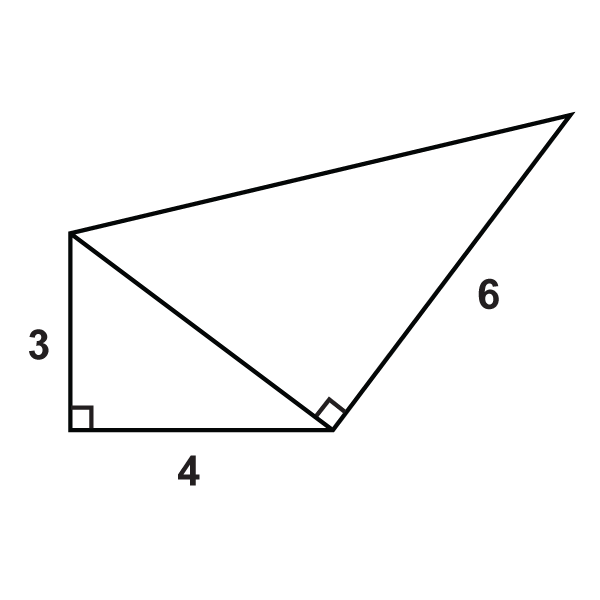
Малюнок\(\PageIndex{14}\)

Використовуйте цифру, щоб відповісти на питання.

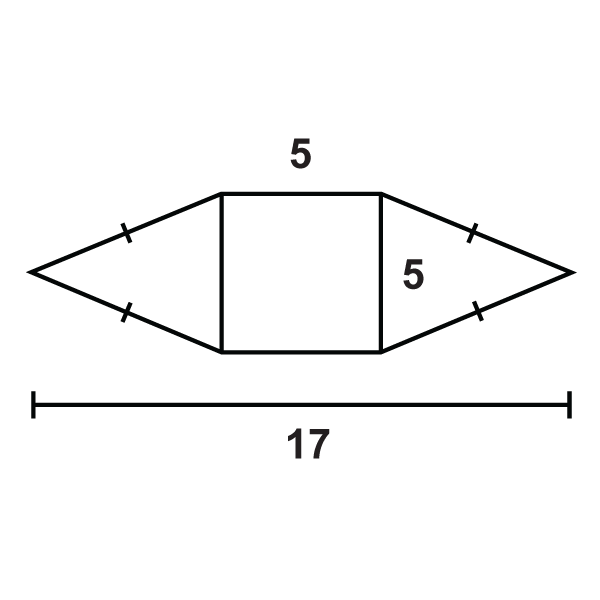
F-д_ДФ БФ 75487Б2Е31 ФЭ2А63 БК 3ЦЕ8Ф де 39 ЕЕЦД 21Ф622С4Б5Д058522 ФАЕ4+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{15}\)

Яка площа площі?
Яка площа трикутника зліва?
Яка площа складеної фігури?

Огляд (Відповіді)

Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 10.6.

Лексика

Термін	Визначення
площа	Обсяг простору всередині фігури. Площа вимірюється в квадратних одиницях.
композитна форма	Форма, що складається з інших фігур.
периметр	Відстань навколо фігури. Периметр будь-якої фігури повинен мати прикріплену до нього одиницю виміру. Якщо конкретних одиниць не вказано (фути, дюйми, сантиметри тощо), запишіть *одиниці.*
Композитний	Число, яке має більше двох факторів.

Додаткові ресурси

Інтерактивний елемент

Відео: Площа трикутника (цілі числа)

Діяльність: Область композитних фігур Питання обговорення

Навчальні посібники: Посібник з вивчення периметра та області

Практика: Площа та периметр композитних фігур