Skip to main content
LibreTexts - Ukrayinska

5.16: Повітряні змії

  1. Last updated
  2. Save as PDF
  • Page ID
    54809

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

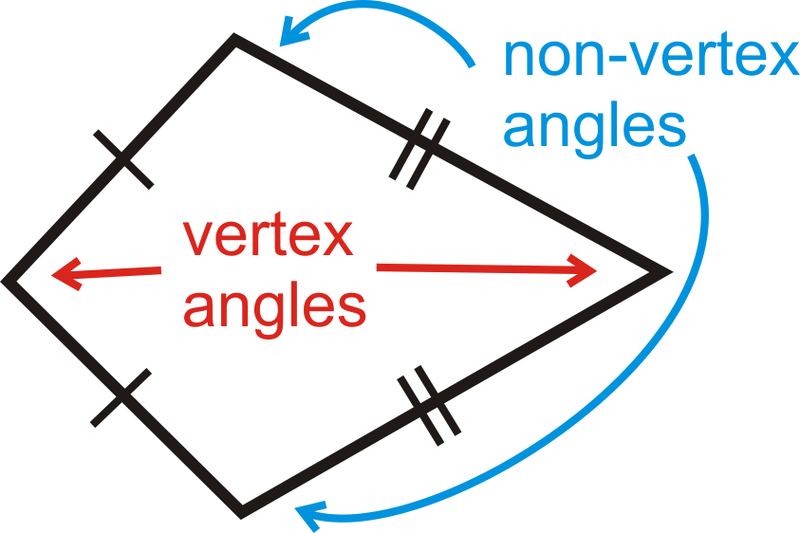
    Чотирикутники з двома різними наборами суміжних, конгруентних сторін.

    Повітряний змій - це чотирикутник з двома чіткими наборами суміжних конгруентних сторін. Він схожий на повітряного змія, який літає в повітрі.

    Ф-Д_60С8БД 87Е1ФК 4854Е22КБФ 680ФБ4ААБ 0ФЕ94317061КФА 679ДФ1БААА7+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    З визначення повітряний змій міг бути увігнутим. Якщо повітряний змій увігнутий, його називають дротиком. Слово відмінне у визначенні означає, що дві пари конгруентних сторін повинні бути різними. Це означає, що квадрат або ромб - це не повітряний змій.

    Кути між конгруентними сторонами називаються кутами вершин. Інші кути називаються невершинними кутами. Якщо ми проведемо діагональ через кути вершин, у нас буде два конгруентних трикутника.

    F-д_д6д4ф6 ДДД296154С7С93БК8ФКА01Б3ДЕ 60С350Е99 БААБ4Е81ЕБ9ДФФАБ+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Факти про повітряних зміїв

    1. Невершинні кути повітряного змія є конгруентними.

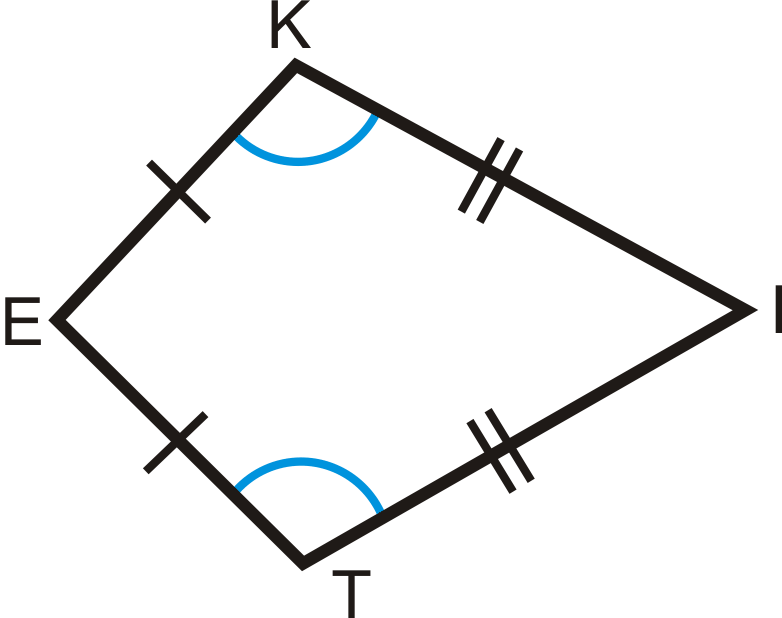
    Ф-д_Б52Д5ДБ1С549А26А1 КДФ 5А55079Ф8Ф4А03Б5Д29Б3432375Е7А607С+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Якщо\(KITE\) це повітряний змій, то\(\angle K\cong \angle T\).

    2. Діагональ через кути вершини - це бісектриса кута для обох кутів.

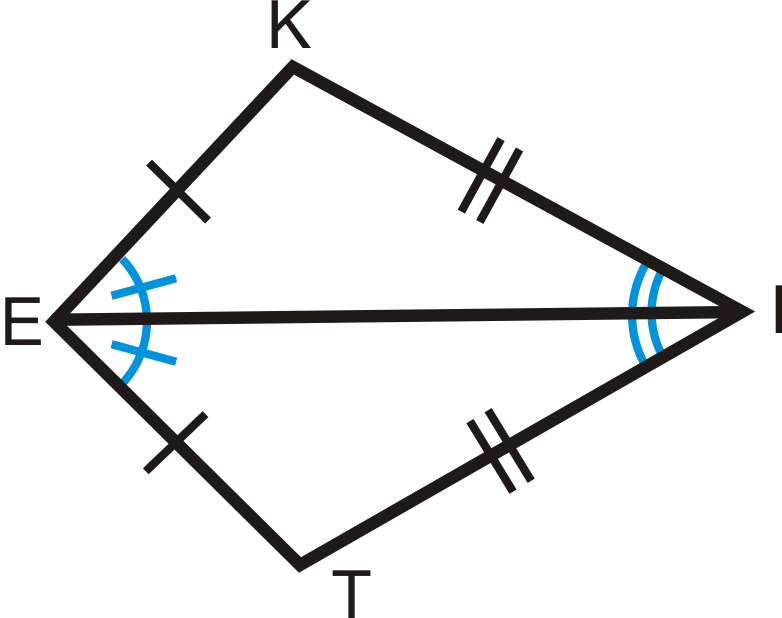    fig-ch01_patchfile_01.jpgФ-д_С98ФФ4Ф 126701656 CD6475002253 ФЕ195ФБ5Е27БФФ68746А4298Ф57E+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{4}\)

    Якщо\(KITE\) це повітряний змій, то\(\angle KEI\cong \angle IET\) і\(\angle KIE\cong \angle EIT\).

    3. Теорема про діагоналі повітряного змія: Діагоналі повітряного змія перпендикулярні.

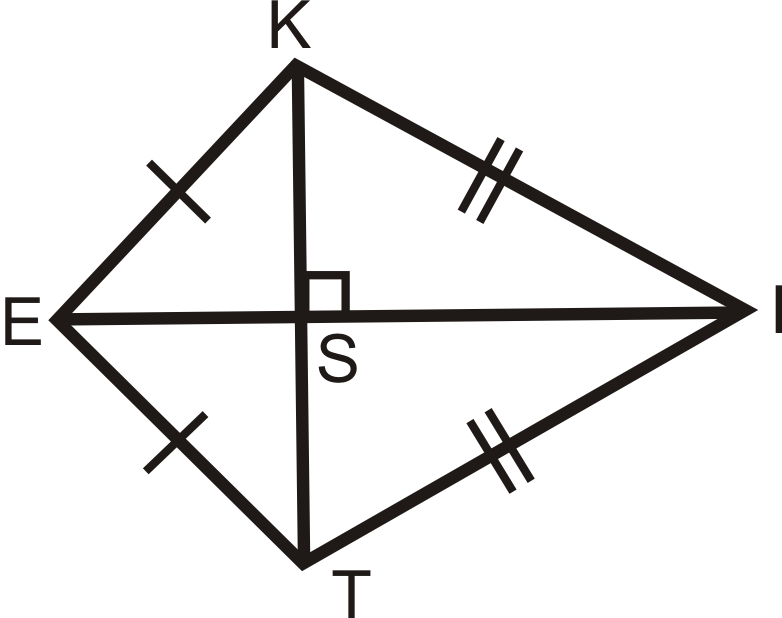    F-D_5DE76164БД0241АФ 62 ФАД 54 ДБ5А11 КДФ 39Б90506008Е4С6Е169С9ЕД0+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{5}\)

    \( \Delta KET\)і\(\Delta KIT\) є рівнобедрені трикутники, так\(\overline{EI}\) і перпендикулярна бісектриса\(\overline{KT}\) (Теорема трикутника рівнобедреного).

    Що робити, якщо вам сказали, що\(WIND\) це повітряний змій, і вам дають інформацію про деякі його кути або його діагоналі? Як би ви знайшли міру інших кутів або його сторін?

    Для прикладів 1 і 2 використовуйте наступну інформацію:

    \(KITE\)це повітряний змій.

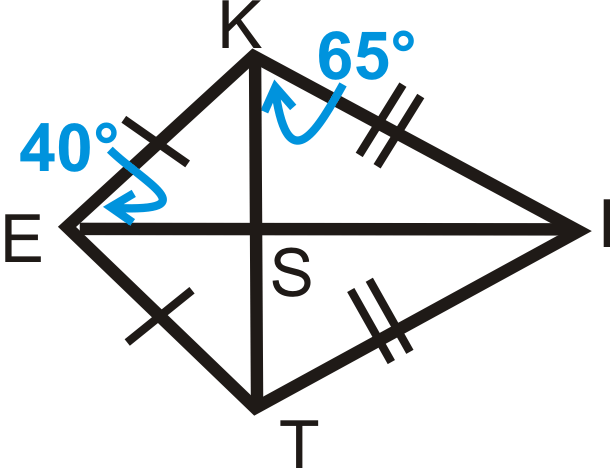
    F-д_82е46ДФ 3242431434707716Ф6Б1266А3Ф63Ф2Ф2ААБ2ААБ2297561Б2Е0ДА+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    Приклад\(\PageIndex{1}\)

    Знайти\(m\angle KIS\).

    Рішення

    \(m\angle KIS=25^{\circ}\)Теорема про суму трикутника (пам'ятайте, що\ кут KSI є прямим кутом, оскільки діагоналі перпендикулярні.)

    Приклад\(\PageIndex{2}\)

    Знайти\(m\angle IST\).

    Рішення

    \(m\angle IST=90^{\circ}\)тому що діагоналі перпендикулярні.

    Приклад\(\PageIndex{3}\)

    Знайдіть відсутні заходи в повітряних зміях нижче.

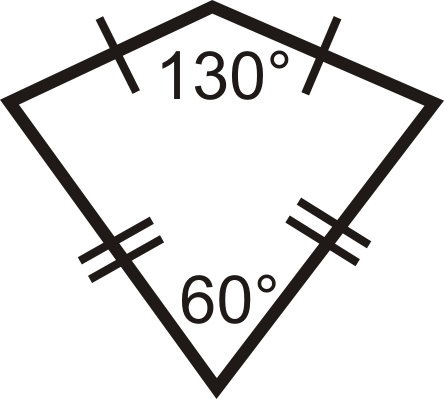
    1. Ф-д_С7 БФ 721826302944С490Е0Д6Д0Д72Д9539013DA1 ЦБДАА0ФБ376+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{7}\)
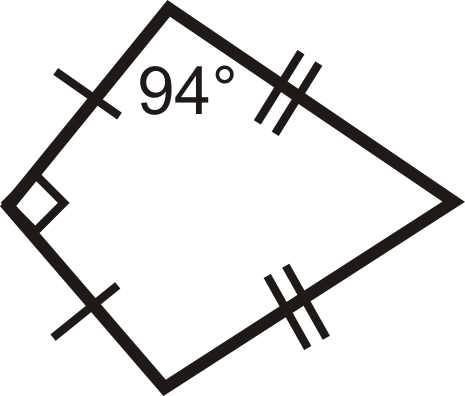
    2. F-д_3855 ЦЭС 2А9С2Се 55С1Ф0Б22С251740728А39С6ФД1018 ББ46Б6+зображення_крихіткий+зображення_крихіткий_крихіткий.PNG
      Малюнок\(\PageIndex{8}\)

    Рішення

    1. Два кути ліворуч - це невершинні кути, які є конгруентними.

      \( \begin{aligned} 130^{\circ} +60^{\circ} +x+x=360^{\circ} \\ 2x&=170^{\circ} \\ x&=85^{\circ} \qquad Both angles are 85^{\circ} \end{aligned}\)

    2. Інший невершинний кут також\(94^{\circ}\). Щоб знайти четвертий кут, відніміть з інших трьох кутів\(360^{\circ}\).

      \(\begin{aligned} 90^{\circ} +94^{\circ} +94^{\circ} +x &=360^{\circ} \\ x&=82^{\circ} \end{aligned}\)

    Приклад\(\PageIndex{4}\)

    Використовуйте теорему Піфагора, щоб знайти довжини сторін повітряного змія.

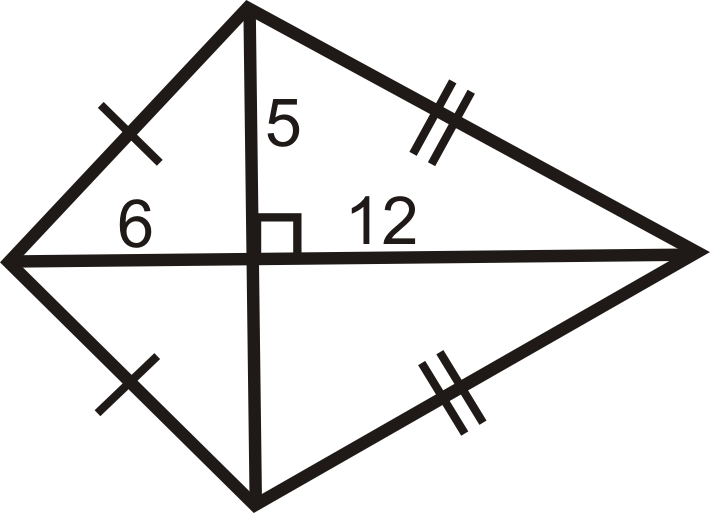
    F-д_8Ф71Е09Б05СД0ФБАА94ФА68Ф698Е442 ПЗД 6Д2997FF4C39D66ЕД41С7+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{9}\)

    Рішення

    Нагадаємо, що теорема Піфагора говорить\(a^2+b^2=c^2\), де\(c\) знаходиться гіпотенуза. У цього повітряного змія сторони - гіпотенузи.

    \ (\ почати {масив} {rr}
    6^ {2} +5^ {2} =h ^ {2} & 12^ {2} +5^ {2} =j^ {2}\
    36+25=h^ {2} & 144+25=j^ {2}\\
    61 = h ^ {2} & 169=j^ {2}\\
    \ sqrt {61} =h & 13=j
    \ кінець {масив}\)

    Приклад\(\PageIndex{5}\)

    Доведіть, що невершинні кути повітряного змія є конгруентними.

    Дано:\(KITE\) з\(\overline{KE}\cong \overline{TE}\) і\(\overline{KI}\cong \overline{TI}\)

    Доведіть:\(\angle K\cong \angle T\)

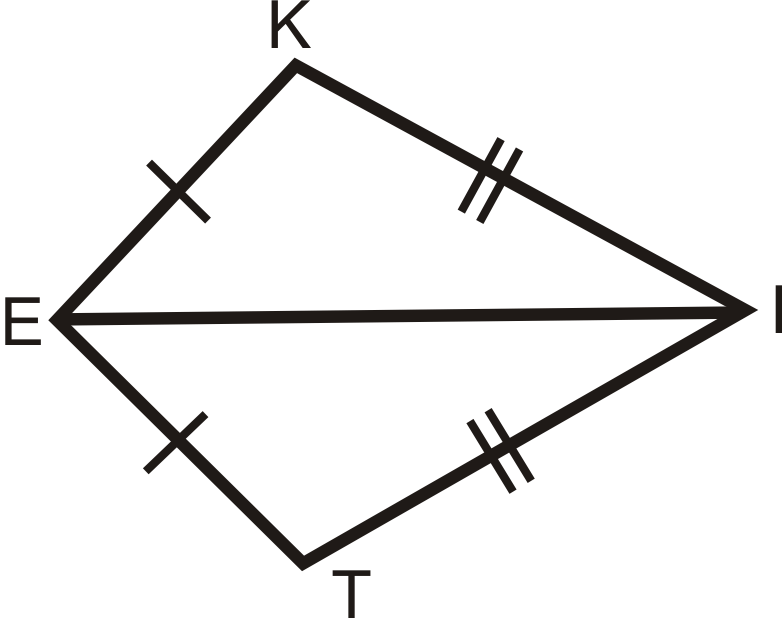
    F-D_4592C1898E9F1C1F2B253997E9652732C7965FDC0CCD791209C87947+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{10}\)

    Рішення

    Заява Причина
    1. \(\overline{KE}\cong \overline{TE}\)і\(\overline{KI}\cong \overline{TI}\) 1. Враховується
    2. \( \overline{EI}\cong \overline{EI}\) 2. Рефлексивний PoC
    3. \(\Delta EKI\cong \Delta ETI\) 3. ССС
    4. \(\angle K\cong \angle T\) 4. CPCTC

    Рецензія

    Для питань 1-6 знайдіть значення відсутньої змінної (ів). Всі фігури - повітряні змії.

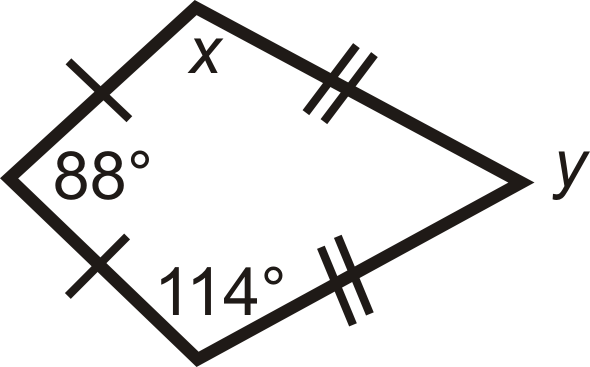
    1. Ф-д_аф 65661 дБФ 574289Д7А5Ф5Д84А6дББ4Д2 АБК 1d4F9ed646387A4+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{11}\)
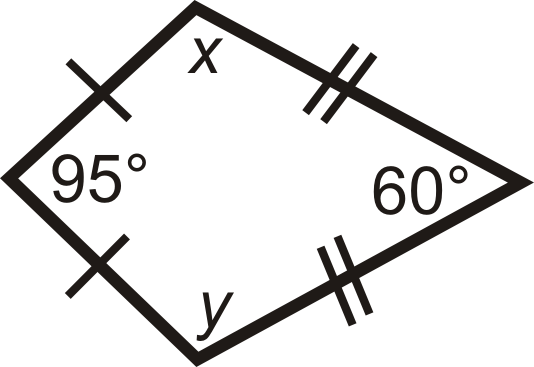
    2. F-д_Ф34Ф5362Ф77С Каб 43203101E4D772058D1D1Б96ФА8 CF2558C3660357A+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)
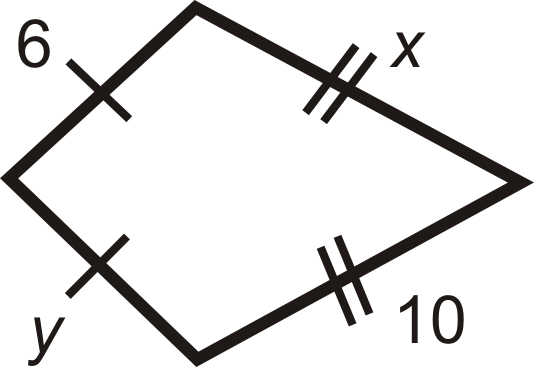
    3. F-D_60E4FC284D4D420AA22C777B48041E76922 Дек 11840558 ДД0988 FFE30D+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)
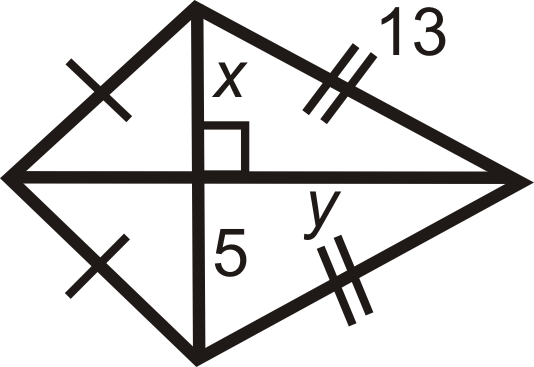
    4. Ф-Д_Д8 БДФ 09Е7Б38 АЕЕ2 Дек 9Ф55500д7 де 006052Ф5Ф60016к34Е504Ф3ФБ0+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{14}\)
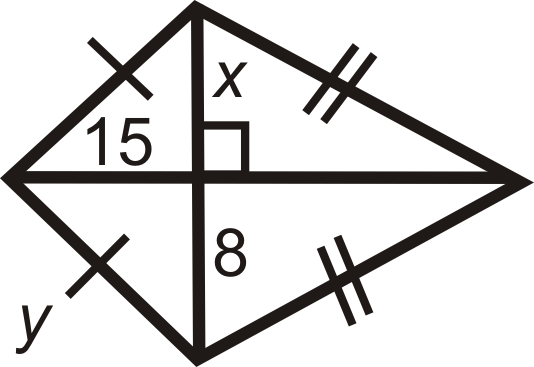    5. F-D_96 Деб 04БФКД 85Е8885629244CF0390a589 ББД7127Е89 ABCD4D8D10D+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{15}\)
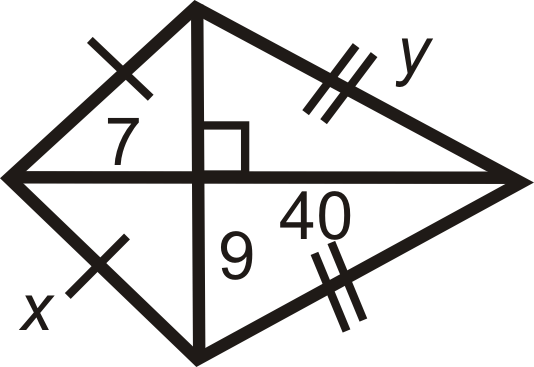
    6. F-д_7Е2Б9308 ККФ Б0Б0Б 1996 С6Е5 А7 БББА Е03А146А965А00ЕД 849Ф904Б1ББ+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{16}\)

    Для питань 7-11 знайдіть значення відсутньої змінної (ів).

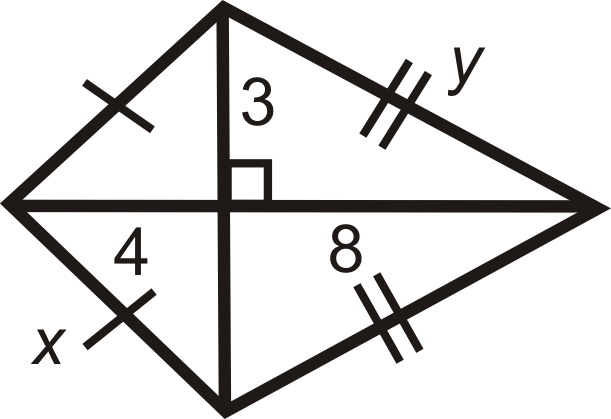
    1. F-д_8ФББ Б 6cd913967512ABBC 364c92895C1ec3789c008665013B174EF0B+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{17}\)
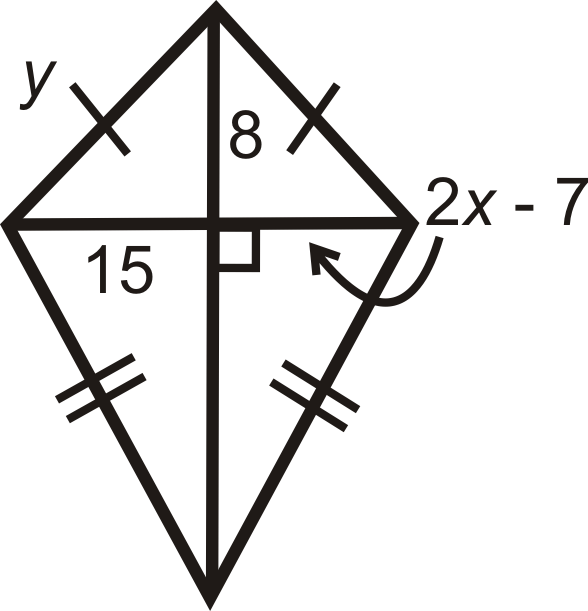
    2. F-д_2ЕС666Д93 АББА А71753АААБС1БД9883А9 СБ808643Е83Е83Б01А070817+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{18}\)
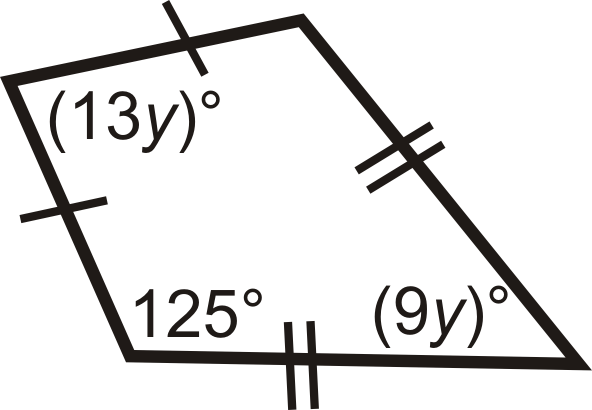
    3. F-д_73 СБ 80999207498101DA9Ф56ЕД ФА749Е3Б2301Д11А6ЕД 03Ф0211720Б+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{19}\)
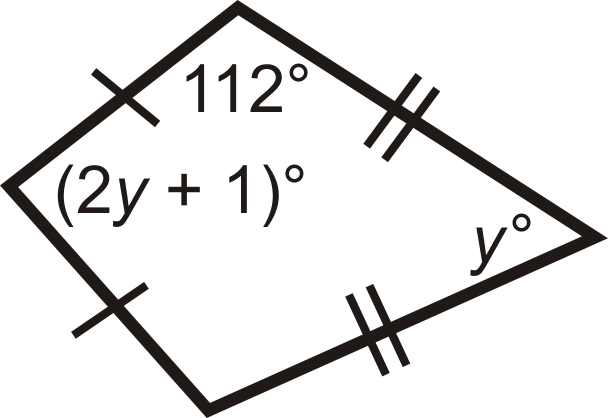
    4. Ф-д_А7С464ФД 0679040Фе 4Д8Ф2ФК 70Е9039А6Б7906C895994895E8E5C654+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{20}\)
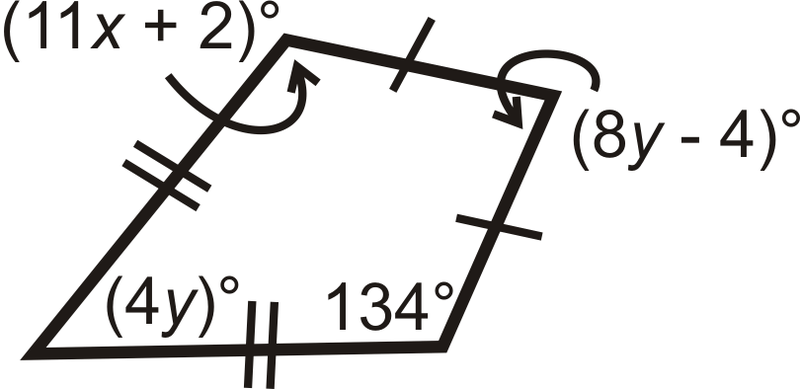
    5. F-D_829935 Де-39ДК6А1Ф 1287Б13Ф6Д31119БФ0БФ0Б92852065329Д11Ф44Б4+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{21}\)
    1. Заповніть пробіли до доказу нижче.

    Дано:\(\overline{KE}\cong \overline{TE}\) і\(\overline{KI}\cong \overline{TI}\)

    Доведіть:\(\overline{EI}\) це бісектриса кута\(\angle KET\) і\(\angle KIT\)

    F-D_4592C1898E9F1C1F2B253997E9652732C7965FDC0CCD791209C87947+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{22}\)
    Заява Причина
    1. \( \overline{KE}\cong \overline{TE} and \overline{KI}\cong \overline{TI}\) 1.
    2. \(\overline{EI}\cong \overline{EI}\) 2.
    3. \(\Delta EKI\cong \Delta ETI\) 3.
    4. 4. CPCTC
    5. \(\overline{EI} is the angle bisector of \angle KET\)і\ кут KIT\) 5.
    1. Заповніть пробіли до доказу нижче.

    Дано:\(\overline{EK}\cong \overline{ET},\: \overline{KI}\cong \overline{IT}\)

    Доведіть:\(\overline{KT}\perp \overline{EI}\)

    F-D_5DE76164БД0241АФ 62 ФАД 54 ДБ5А11 КДФ 39Б90506008Е4С6Е169С9ЕД0+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{23}\)
    Заява Причина
    1. \(\overline{KE}\cong \overline{TE}\)і\(\overline{KI}\cong \overline{TI}\) 1.
    2. 2. Визначення рівнобедрених трикутників
    3. \(\overline{EI}\)це бісектриса кута\(\angle KET\) і\(\angle KIT\) 3.
    4. 4. Теорема про рівнобедрене трикутник
    5. \(\overline{KT}\perp \overline{EI}\) 5.

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 6.7.

    Лексика

    Термін Визначення
    повітряний змій Чотирикутник з чіткими суміжними конгруентними сторонами.
    Теорема про суму трикутника Теорема про суму трикутника стверджує, що три внутрішні кути будь-якого трикутника складають до 180 градусів.
    Вертикальні кути Вертикальні кути - це пара протилежних кутів, створених пересічними лініями.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Принципи повітряних зміїв - Основні

    Види діяльності: Запитання для обговорення повітряних зміїв

    Навчальні посібники: Посібник з вивчення трапецій та повітряних зміїв

    Практика: повітряних зміїв

    Реальний світ: йти літати повітряного змія