5.14: Площа і периметр трапецій

Last updated
Save as PDF

Page ID: 54869

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Площа - висота, що перевищує середнє значення підстав; периметр - сума сторін.

Трапеція - це чотирикутник з однією парою паралельних сторін. Паралельні сторони називаються підставами, і ми будемо називати довжини підстав як\(b_1\) і\(b_2\). Перпендикулярна відстань між паралельними сторонами - це висота трапеції. Площа трапеції - це те,\(A=\dfrac{1}{2}h(b_1+b_2)\) де\(h\) завжди перпендикулярно підставах.

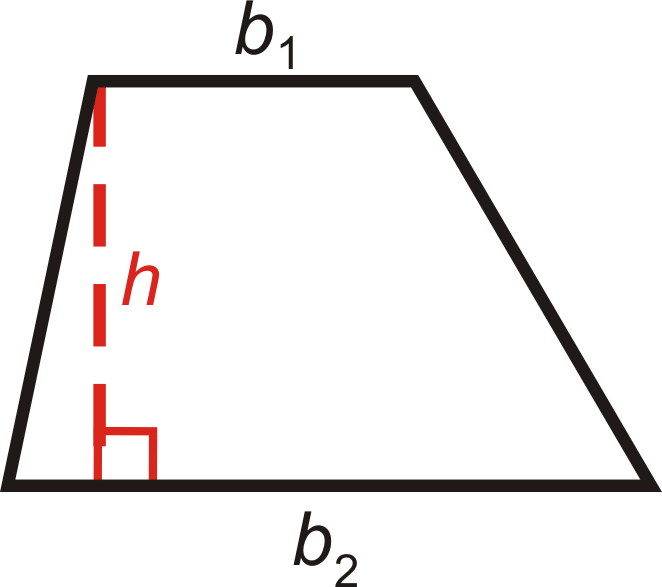
F-D_C1B06AB493БФБ762СЕ7А00292 ЕЕБ9ФД1Д51740ЕД 61874 BE55029F0E3+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{1}\)

Що робити, якщо вам дали трапецію і розмір двох її основ, а також її висоту? Як ви могли знайти загальну відстань навколо трапеції та кількість місця, яке вона займає?

Приклад\(\PageIndex{1}\)

Знайдіть площу трапеції.

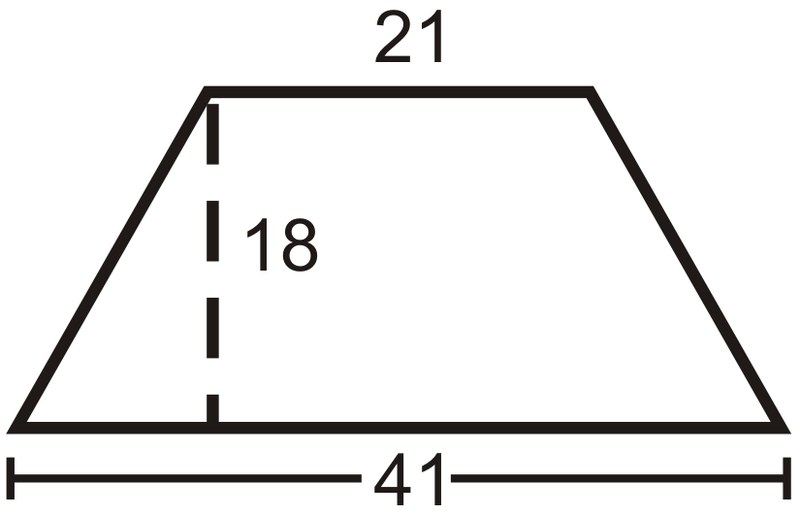
F-д_Е764Ф1С3Е83Б3024ККА 4С061 ЦББ 134Б БББ 2А05Ф4ФД30FF0782ЕД47F8+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

Рішення

Скористайтеся формулою для площі трапеції.

\(\dfrac{1}{2}(18)(41+21)=558\text{ units}^2\)

Приклад\(\PageIndex{2}\)

Знайдіть площу трапеції. Округляйте свої відповіді до найближчих сотих.

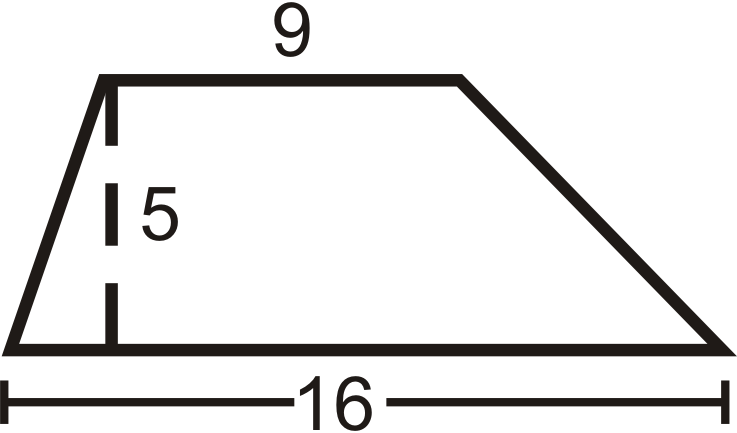
F-D_0 ДБК04261СА9 БББББ2 ЕБФ 8С4КД0Д 2ЕД 01КБС415Д971С874БФ94805F3E+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{3}\)

Рішення

Скористайтеся формулою для площі трапеції.

\( \dfrac{1}{2}(5)(16+9)=62.5\text{ units}^2\)

Приклад\(\PageIndex{3}\)

Знайдіть площу трапеції.

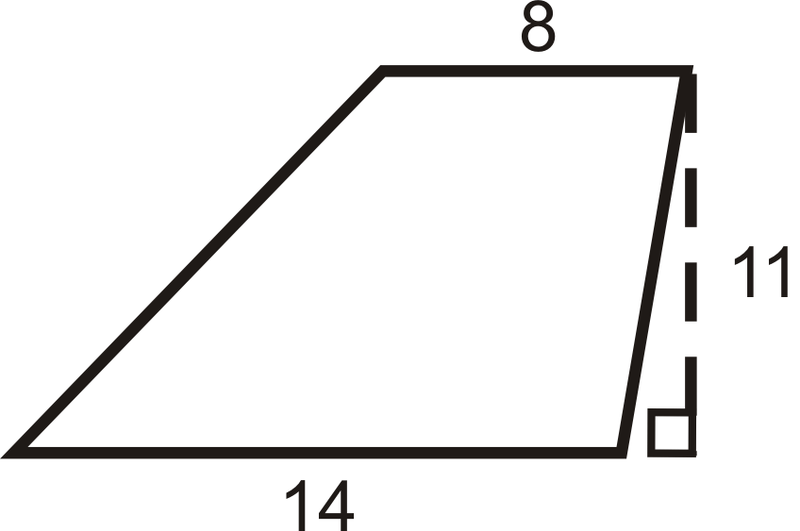
F-D_93929731E81FCCB Б Б 0Е48ЕС65С76ЦБ9ДЕ3070945АА96CA9E6764CF7+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{4}\)

Рішення

\(\begin{aligned} A&=\dfrac{1}{2}(11)(14+8) \\ A&=\dfrac{1}{2}(11)(22) \\ A&=121\text{ units}^2\end{aligned}\)

Приклад\(\PageIndex{4}\)

Знайдіть площу трапеції.

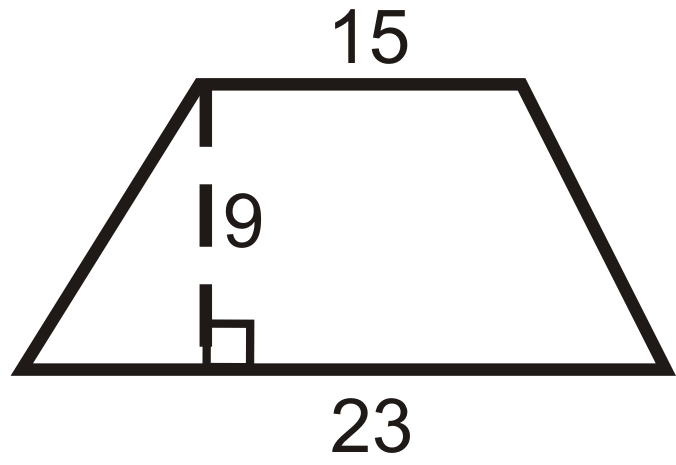
Ф-Д_57Е55КБ65БА 8А0С7Ф53Е1А46Ф74 ФФ 5Ф49301CDF6988BCBFD9A444A1+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{5}\)

Рішення

\(\begin{aligned} A&=\dfrac{1}{2}(9)(15+23) \\ A&=\dfrac{1}{2}(9)(38) \\ A&=171\text{ units}^2 \end{aligned}\)

Приклад\(\PageIndex{5}\)

Знайдіть периметр і площу трапеції.

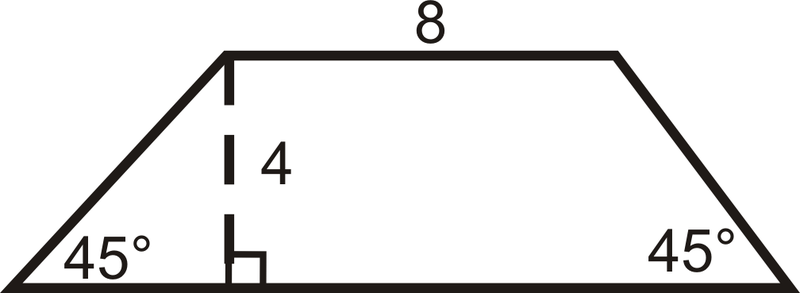
F-D_4A742E4F3D7FFE2227D6c71cd 43АБ769ФД Додано БФБ899185ЕЕЕБ566908+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{6}\)

Рішення

Незважаючи на те, що нам не сказали довжину другої основи, ми можемо знайти її за допомогою спеціальних прямих трикутників. Обидва трикутника на кінцях цієї трапеції є рівнобедреними прямими трикутниками, тому гіпотенуси є,\(4\sqrt{2}\) а інші катети довжиною 4.

\(\begin{aligned} P&=8+4\sqrt{2}+16+4\sqrt{2} &\qquad A&=\dfrac{1}{2}(4)(8+16) \\ P&=24+8\sqrt{2}\approx 35.3\text{ units} & A&=48\text{ units}^2 \end{aligned}\)

Рецензія

Знайдіть площу і периметр наступних фігур. Округляйте свої відповіді до найближчих сотих.

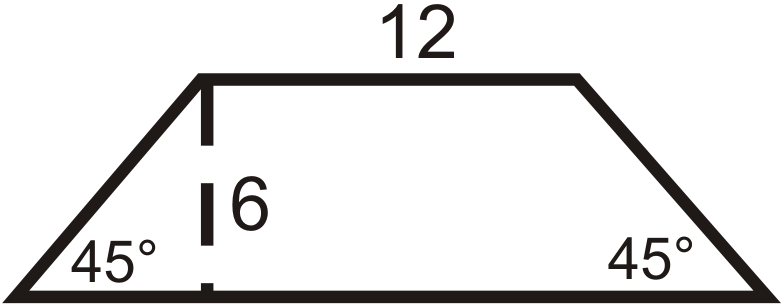
Малюнок\(\PageIndex{7}\)
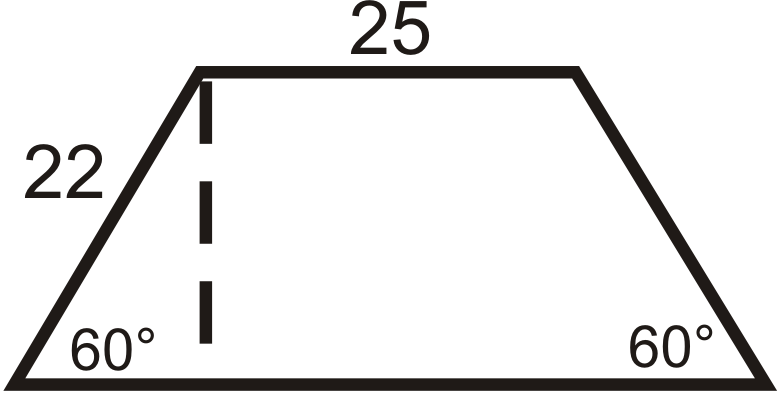
Малюнок\(\PageIndex{8}\)

Знайдіть площу наступних трапецій.

Трапеція з підставами 3 дюйма і 7 дюймів і висотою 3 дюйма.
Трапеція з підставами 6 дюймів і 8 дюймів і висотою 5 дюймів.
Трапеція з підставами 10 дюймів і 26 дюймів і висотою 2 дюйма.
Трапеція з підставами 15 дюймів і 12 дюймів і висотою 10 дюймів.
Трапеція з підставами 4 дюйма і 23 дюйма і висотою 21 дюйм.
Трапеція з підставами 9 дюймів і 4 дюйма і висотою 1 дюйм.
Трапеція з підставами 12 дюймів і 8 дюймів і висотою 16 дюймів.
Трапеція з підставами 26 дюймів і 14 дюймів і висотою 19 дюймів.

Використовуйте наведені цифри, щоб відповісти на питання.

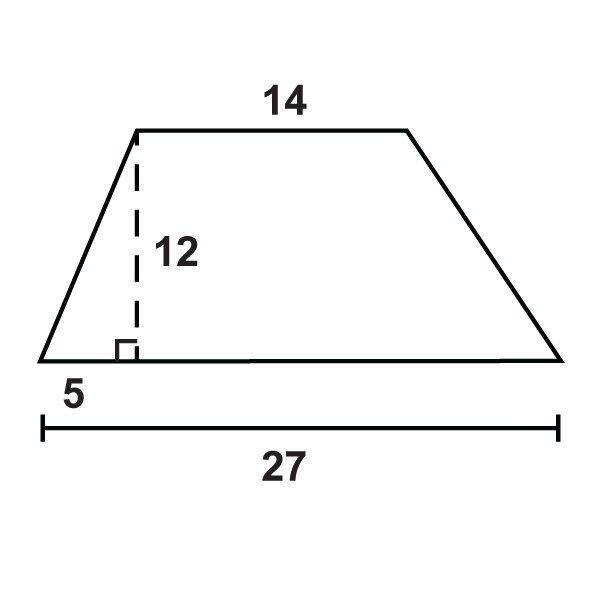
F-д_66ф 889271да061С075Е7Ф3293 ЕЦДБД11ДЕ4Ф7КА927Ф17Д80АЦ954Б9Ф+зображення_крихіткий+зображення_крихіткий_PNG — Малюнок\(\PageIndex{9}\)

Який периметр трапеції?
Яка площа трапеції?

F-D_3АА 86122Б2468А 1535858022292851 БД15 БББК 4Б5833Ф747818А0Ф11+зображення_крихіткий+зображення_крихіткий_png — Малюнок\(\PageIndex{10}\)

Який периметр трапеції?
Яка площа трапеції?

F-д_ДД33 де 75С7638 БК 7Е2Е588FF9 Дед С1Е5Е5675А9Ф13703529771 ЕА31+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{11}\)

Який периметр трапеції?
Яка площа трапеції?

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 10.5.

Лексика

Термін	Визначення
площа	Обсяг простору всередині фігури. Площа вимірюється в квадратних одиницях.
рівнобедрений трапеції	*Рівнобедрений трапеція* - це трапеція, де непаралельні сторони конгруентні.
середньосегментний (трапеції)	Відрізок лінії, який з'єднує середні точки непаралельних сторін.
периметр	Відстань навколо фігури. Периметр будь-якої фігури повинен мати прикріплену до нього одиницю виміру. Якщо конкретних одиниць не вказано (фути, дюйми, сантиметри тощо), запишіть *одиниці.*
трапеція	Чотирикутник з рівно однією парою паралельних сторін.

Додаткові ресурси

Інтерактивний елемент

Відео: Приклади площі і периметра трапецій - Основні

Види діяльності: Площа та периметр трапецій Питання обговорення

Навчальні посібники: Трикутники та чотирикутники Навчальний посібник

Практика: Площа і периметр трапецій

Реальний світ: Периметр