Skip to main content
LibreTexts - Ukrayinska

5.13: Трапеції

  1. Last updated
  2. Save as PDF
  • Page ID
    54850

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Визначте невідомі кутові вимірювання чотирикутників з рівно однією парою паралельних сторін.

    Трапеція - це чотирикутник з рівно однією парою паралельних сторін.

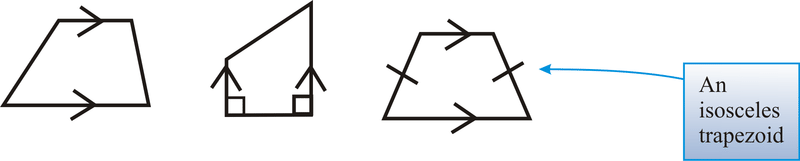
    Ф-д_85да 86Б74Д3Е7КФ 769А38ЕД 51БФ8 А9ДД6БФБ 06Б142С8100BE848+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Рівнобедрений трапеція - це трапеція, де непаралельні сторони конгруентні.

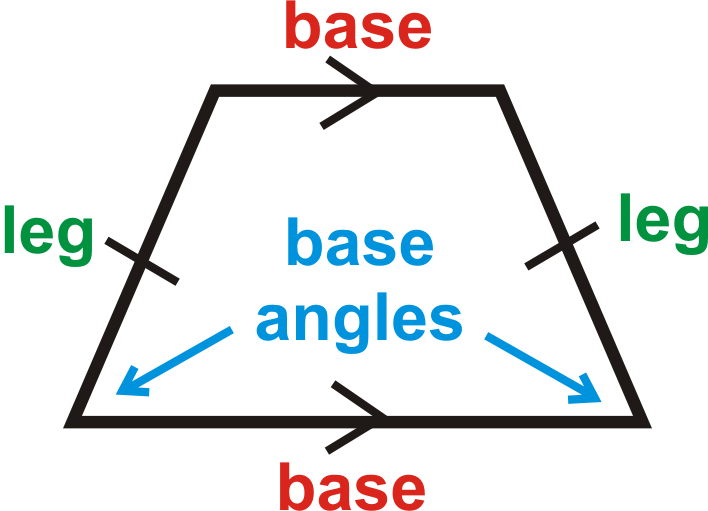
    F-D_6692d09 BBB Бджола EFE05E18E626314C63Б9С7С8Ф412A3290EE10CAE837D+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Базові кути рівнобедреної трапеції конгруентні. Якщо\(\(ABCD\)\) - рівнобедрений трапеція, то\(\angle A\cong \angle B\) і\(\angle C\cong \angle D\).

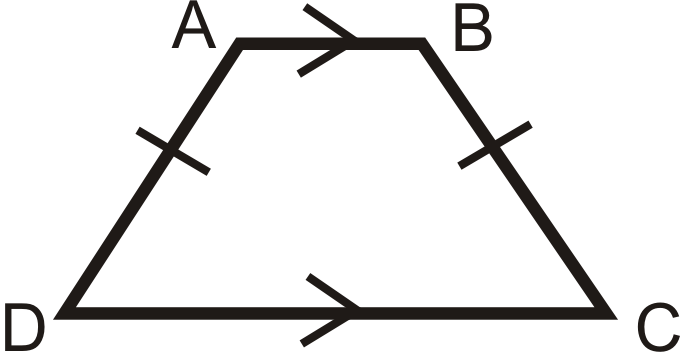
    Ф-Д_90АД 2КС 14 Дек ДД426ФБ2Б247Е7621150 Постійний струм 950854Е8КФ 4Ф11Б876+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Зворотне також вірно. Якщо трапеція має конгруентні кути підстави, то вона являє собою рівнобедрену трапецію. Діагоналі рівнобедреної трапеції також конгруентні. Середній сегмент (трапеції) - це відрізок лінії, який з'єднує середні точки непаралельних сторін:

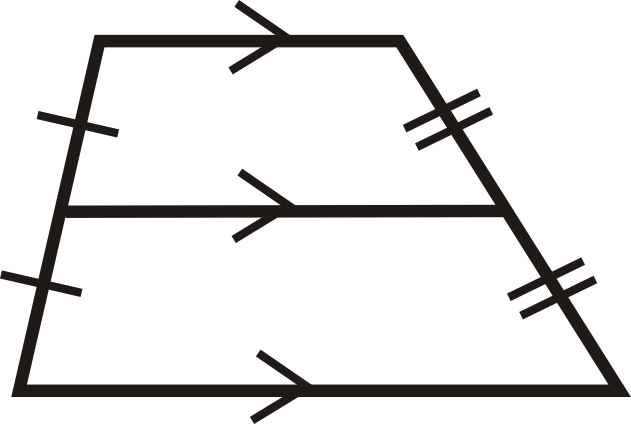
    F-д_Е7С3Ф7Д0Ф75ДК3Е68ЕБ9А47 ААА3А09А4805Ф24ФФФФБ011+зображення_крихіткий+зображення_крихіткий_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    У трапеції є тільки один серединний сегмент. Вона буде паралельна підставам, оскільки розташована на півдорозі між ними.

    Теорема середнього сегмента: Довжина середнього сегмента трапеції - це середнє значення довжин підстав.

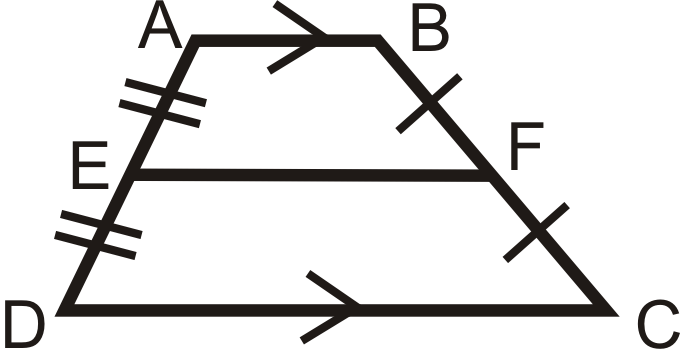
    Ф-д_Е9Б587Е86482Ф04КБ836938279 АФ Ф 16БК 94Е5Ф454261БД57ФЕ7026E+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Якщо\(\overline{EF}\) це серединний сегмент, то\(EF=\dfrac{AB+CD}{2}\).

    Що робити, якщо вам сказали, що багатокутник\(ABCD\) - це рівнобедрений трапеція і що один з його базових кутів вимірює\(38^{\circ}\)? Що можна зробити висновок про інший його базовий кут?

    Для прикладів 1 і 2 використовуйте наступну інформацію:

    \(\(TRAP\)\) - рівнобедрений трапеція.

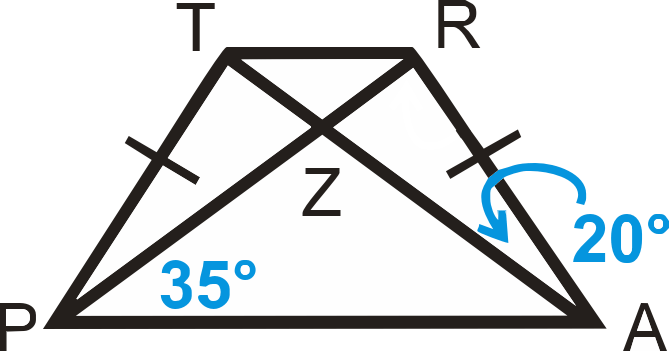
    F-D_C00АСЕ 22483D21997564БДДД 94C062ДФ030А05д979ec7c7c55246C+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    Приклад\(\PageIndex{1}\)

    Знайти\(m\angle TPA\).

    Рішення

    \(\angle TPZ\cong \angle RAZ\)так\(m\angle TPA=20^{\circ} +35^{\circ} =55^{\circ}\).

    Приклад\(\PageIndex{2}\)

    Знайти\(m\angle ZRA\).

    Рішення

    Так як\(m\angle PZA=110^{\circ}\),\(m\angle RZA=70^{\circ}\) тому що вони утворюють лінійну пару. За теоремою про суму трикутника,\(m\angle ZRA=90^{\circ}\).

    Приклад\(\PageIndex{3}\)

    Подивіться на трапецію\(TRAP\) нижче. Що таке\(m\angle A\)?

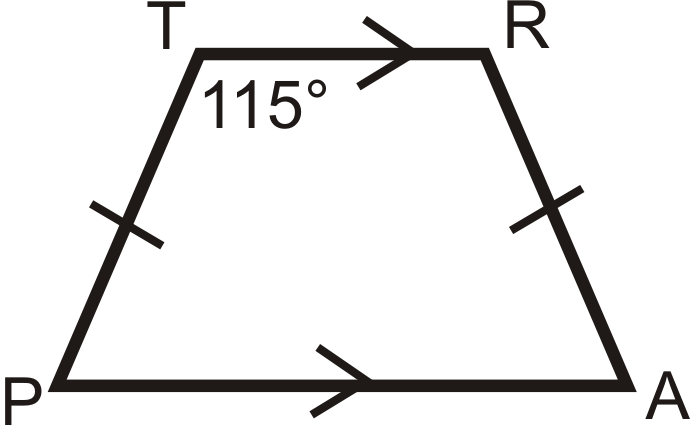
    Ф-д_БФБ1А 31БД2Ф7Б79971801БК 7С3С3ДББ 4Б00А51Е4А6 Каф107С9Ф032С+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{7}\)

    Рішення

    \(TRAP\)являє собою рівнобедрену трапецію. \(m\angle R=115^{\circ}\)також.

    Щоб знайти\ (m\ кут), встановіть рівняння.

    \ (\ почати {вирівняний}
    115^ {\ circ} +115^ {\ circ} +м\ кут A+м\ кут P &= 360^ {\ circ}\
    230^ {\ circ} +2 м\ кут A &= 360^ {\ circ}\ quad\ правий стрілка m\ кут A = M\ кут P\\
    2 м\ кут A &= 130^ {circ}\\
    м\ кут A &=65^ {\ circ}
    \ кінець { вирівняні}\)

    Зауважте, що\(m\angle R+m\angle A=115^{\circ} +65^{\circ} =180^{\circ}\). Ці кути завжди будуть додатковими через теорему про послідовні внутрішні кути.

    Приклад\(\PageIndex{4}\)

    Це\(ZOID\) рівнобедрений трапеція? Звідки ти знаєш?

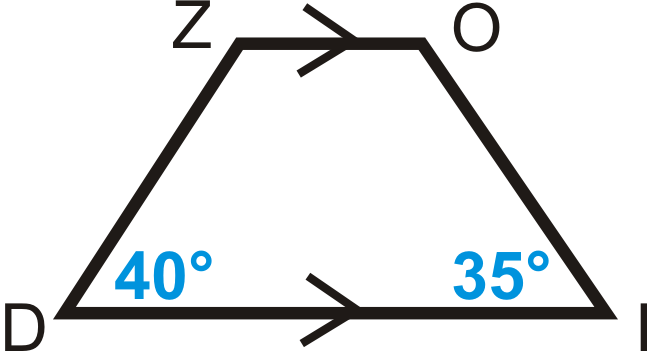
    F-D_053AD 68C2D327C0FE2250DAE3F8075E1A661132B22A972E194EC02D+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{8}\)

    Рішення

    \(40^{\circ} \neq 35^{\circ}\), Не\(ZOID\) є рівнобедреною трапецією.

    Приклад\(\PageIndex{5}\)

    Знайти\(x\). Всі фігури - трапеції з позначеним середнім сегментом, як зазначено.

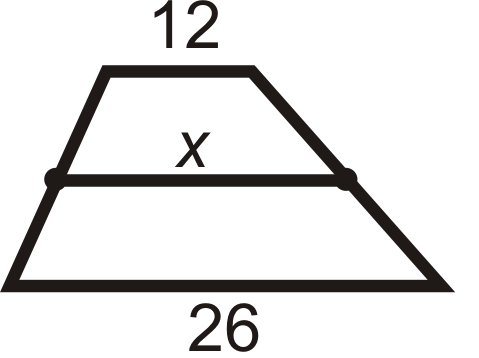
    1. F-д_75А8А92Е617Фе 446439515147Е845ДФ 56ЕД7391А470108614БД12810+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{10}\)
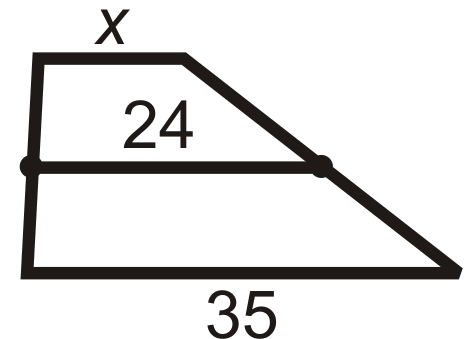
    1. F-D_7671594 А2С974АА4А516А82ДДФ 87С05А2А433848Ф47ФС3853Б0+зображення_крихіткий+зображення_крихітковий_крихіткий.PNG
      Малюнок\(\PageIndex{10}\)
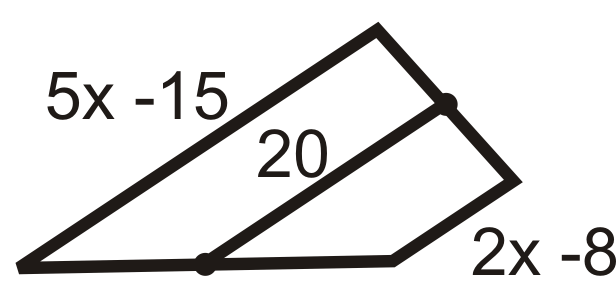
    2. Ф-Д_САА 24327458 ДК 5Ф2Ф7С1АЕЕ9220318 БД2822 ФФ11С72Ф9Ф042517DE3+зображення_крихіткий+зображення_крихіткий_PNG
      Малюнок\(\PageIndex{11}\)

    Рішення

    1. \(x\)це середнє значення 12 і 26. \(\dfrac{12+26}{2}=\dfrac{38}{2}=19\)
    2. 24 - це середнє значення\(x\) і 35.

      \(\begin{aligned} \dfrac{x+35}{2}&=24 \\ x+35&=48 \\ x&=13 \end{aligned}\)

    1. 20 - це середнє значення\(5x−15\) і\(2x−8\).

      \(\begin{aligned} \dfrac{5x−15+2x−8}{2}&=20 \\ 7x−23&=40 \\ 7x&=63 \\ x&=9 \end{aligned}\)

    Рецензія

    1. Чи можуть паралельні сторони трапеції бути конгруентними? Чому чи чому ні?

    Для питань 2-8 знайдіть довжину серединногосегмента або відсутньої сторони.

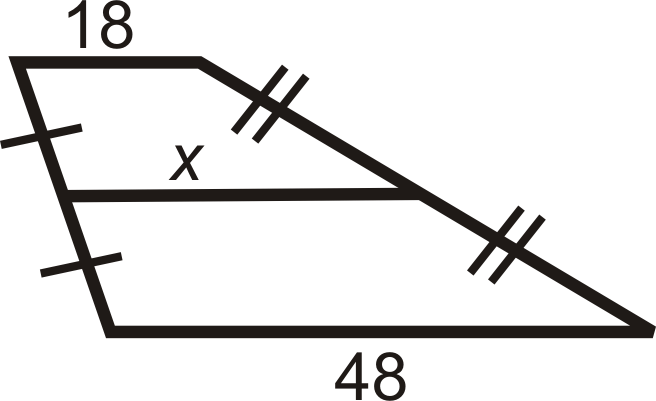
    1. Ф-Д_8174А765Е88593 КС3813А93996d59D59D00778 А43С891ДФ8ДД62763Ф3С+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)
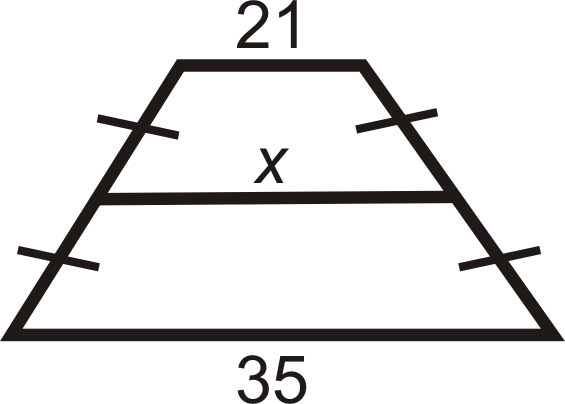
    2. F-D_6C1BE5А 5СБ 93433E44642 куб.см до 4Д3ФЧ 2078Д65630Б2БК67ФДКБ642Б+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)
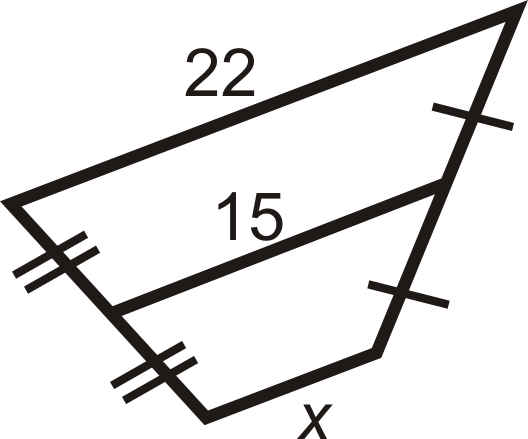
    3. F-д_3Ф8А6Е3Е1 Дас 669Ф1Д9169Б634 ЕБД2А8Б4ФД5Б60С787C076E66+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{14}\)
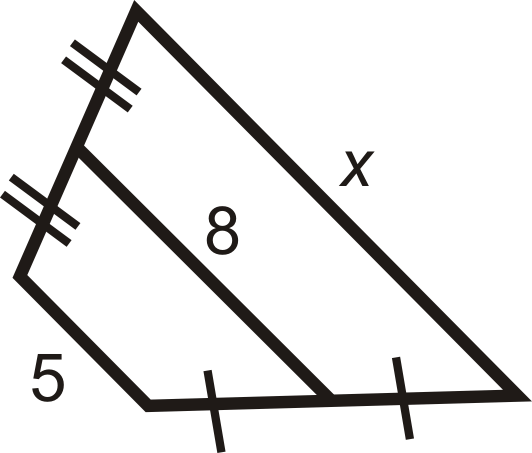
    4. F-д_Е91КС91905С3158А1д 484657596C6C91E9E9699AF769B969+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{15}\)
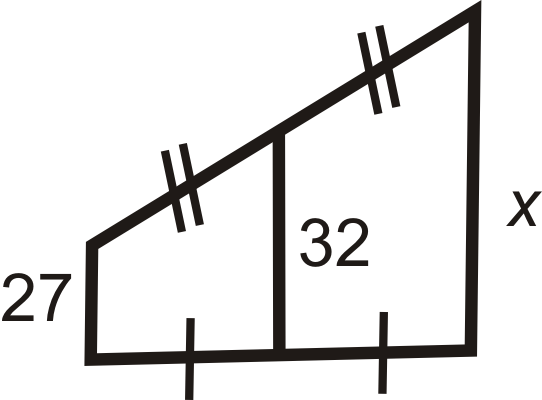
    5. F-д_54789 Фе 8635 КС70 ЕБФ 85 ЕБФ 2ФД18981ДФ 3С414380Д8А009А844А714+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{16}\)
    6. F-д_0ф0366c36473d55c378e18f078a63ad070a7205a5A5b3775c7B2C34F0+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{17}\)

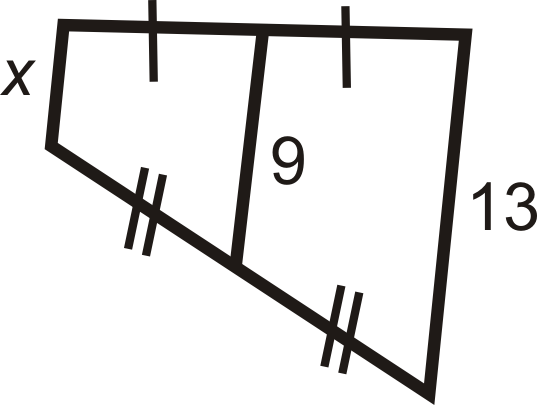
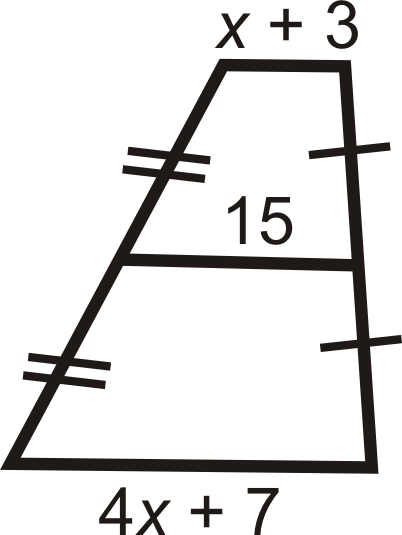
    Знайти значення відсутньої змінної (ів).

    1. F-D_74 АЦ3С5215Д4А2852С000ББ03739АА1АА53629С2628D05C7C5+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{18}\)

    Знайдіть довжини діагоналей трапецій нижче, щоб визначити, чи рівнобедрений він.

    1. A (−3,2), B (1,3), C (3, −1), D (−4, −2)
    2. A (−3,3), B (2, −2), C (−6, −6), D (−7,1)

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 6.6.

    Лексика

    Термін Визначення
    рівнобедрений трапеції Рівнобедрений трапеція - це трапеція, де непаралельні сторони конгруентні.
    середній сегмент (трапеції) Відрізок лінії, який з'єднує середні точки непаралельних сторін.
    трапеція Чотирикутник з рівно однією парою паралельних сторін.
    Діагональ Діагональ - це відрізок лінії в багатокутнику, який з'єднує непослідовні вершини.
    середній сегмент Середній сегмент з'єднує середні точки двох сторін трикутника або непаралельних сторін трапеції.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Приклади трапецій - Основні

    Види діяльності: Трапеції Питання обговорення

    Навчальні посібники: Посібник з вивчення трапецій та повітряних зміїв

    Практика: Трапеції

    Реальний світ: Трапеції в Тімбукту