Skip to main content
LibreTexts - Ukrayinska

5.11: Невідомі розміри паралелограмів

  1. Last updated
  2. Save as PDF
  • Page ID
    54810

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Використовуйте формулу для\(A = bh\) розв'язання невідомої змінної

    F-D_97D4A086730186409014094 ДДБ202Ф33Б9Е482Е9ДД062Д9Е8C800A4+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_jpg
    Малюнок\(\PageIndex{1}\)

    Майкл відповідає за розробку банера для шкільних заходів повернення додому. Банер буде розділений на 4 різні кольорові паралелограми, кожен з яких представляє різний сорт. Дизайн банера в стилі ковдри вимагає, щоб кожен з паралелограм мав площу не менше 720 квадратних дюймів і основу 36 дюймів. Як Майкл може використовувати цю інформацію для визначення мінімальної висоти кожного паралелограма?

    У цій концепції ви дізнаєтеся, як знайти невідомі розміри паралелограмів з урахуванням площі та іншого виміру.

    Знаходження невідомих розмірів паралелограмів

    Знаходження відсутніх розмірів в паралелограмах вимагає від вас роботи назад. Ви можете визначити відсутній розмір, якщо вам дали площу та інше вимірювання, наприклад, площа та висота або площа та основа.

    Площа паралелограма визначається множенням підстави і висоти.

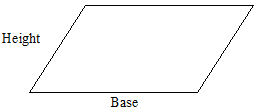
    F-D_AB4C7118E9FF1A9B7FE5B89E2D8AF0A1725721063b3B91B9B22C+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{2}\)

    \(\text{ Base} \times \text{ Height }= \text{ Area of a parallelogram}\)

    Якщо ви знаєте площу і підставу або площа і висоту, ви можете використовувати цю формулу і поділ, щоб знайти відсутній розмір.

    Почнемо з паралелограма, де основою є відсутня розмірність.

    Паралелограм має площу 48 квадратних дюймів і висоту 6 дюймів. Що таке вимір підстави?

    Спочатку підставляємо відому інформацію в формулу обчислення площі паралелограма.

    \(\begin{aligned} \text{ Base} \times \text{ Height } &= \text{ Area of a parallelogram} \\ \text{ Base }\times 6 \text{ inches } &=48\text{ square inches } \end{aligned}\)

    Далі, щоб отримати основу самостійно з одного боку знака рівності, розділіть обидві сторони на відому висоту, 6 дюймів.

    \(\dfrac{\text{ Base } (6\text{ inches })}{6\text{ inches }}=\dfrac{48\text{ square inches }}{6\text{ inches }}\)

    У лівій частині рівняння 6 дюймів скасують залишення основи. У правій частині рівняння 48 квадратних дюймів ділять на 6 дюймів, залишаючи 8 дюймів.

    База = 8 дюймів

    Відповідь - база - 8 дюймів.

    Щоб знайти відсутню базу, ви просто розділили площу на задану висоту. Це буде працювати так само, якщо ви шукаєте висоту. Щоб знайти відсутню висоту, розділіть площу на задану основу.

    Розглянемо цей паралелограм, де висота є відсутнім розміром.

    Паралелограм має площу 54 квадратних футів і підставу 9 футів. Яка висота паралелограма?

    Почніть з роботи назад.

    Щоб знайти відсутню висоту, розділіть задану площу на задане базове вимірювання.

    \(54\div 9=6\)

    Висота паралелограма - 6 футів.

    Приклад\(\PageIndex{1}\)

    Раніше вам дали проблему про Майкла та банер повернення додому.

    Банер буде висіти біля входу в школу протягом тижня повернення додому, тому Михайло хоче переконатися, що кожен клас представлений однаково на банері. Кожен з 4 паралелограм повинен мати мінімальну площу 720 квадратних дюймів і встановлену базу 36 дюймів, а це означає, що Майкл повинен визначити мінімальну висоту кожного паралелограма, щоб забезпечити вимоги до площі. Він вирішує використовувати формулу площі для паралелограмів, щоб знайти відсутню розмірність.

    Рішення

    Спочатку він підставляє відому інформацію в формулу обчислення площі паралелограма.

    \(\begin{aligned} \text{ Base} \times \text{ Height } &= \text{ Area of a parallelogram} \\ 36\text{ inches }\times \text{ Height } &= 720 \text{ square inches } \end{aligned}\)

    Далі, щоб отримати основу самостійно з одного боку знака рівності, розділіть обидві сторони на відому висоту, 6 дюймів.

    \(\dfrac{(36\text{ inches })\text{ Height}}{36 \text{ inches }}=\dfrac{720 \text{ square inches }}{36 \text{ inches}}\)

    Зверніть увагу, що Майкл розділив дану область на задану базу, щоб знайти відсутню висоту.

    \(720\div 36=20\)

    \(\text{ Height} = 20\text{ inches }\)

    Відповідь - мінімальна висота паралелограмів повинна бути 20 дюймів.

    Приклад\(\PageIndex{2}\)

    Знайти відсутню розмірність паралелограма.

    Площа паралелограма становить 169 квадратних дюймів. Довжина підстави - 13 дюймів. Яка висота?

    Рішення

    Спочатку підставляємо відому інформацію в формулу обчислення площі паралелограма.

    \(\begin{aligned} \text{ Base} \times \text{ Height } &= \text{ Area of a parallelogram} \\ 13\text{ inches }\times \text{ Height } &=169 \text{ square inches } \end{aligned} \)

    Далі, щоб отримати основу самостійно з одного боку знака рівності, розділіть обидві сторони на відому висоту, 6 дюймів.

    \(\dfrac{(13\text{ inches }) \text{ Height }}{13\text{ inches }}=\dfrac{169\: \text{ square inches }}{13\text{ inches }}\)

    Зверніть увагу, що ви просто розділили дану область на задану базу, щоб знайти відсутню висоту.

    \(169\div 13=13\)

    \(\text{ Height }= 13\text{ inches }\)

    Відповідь - висота - 13 дюймів.

    Приклад\(\PageIndex{3}\)

    Знайдіть відсутню розмірність паралелограма за допомогою заданих вимірювань.

    Площа = 25 квадратних метрів

    База = 5 метрів

    Рішення

    Спочатку розділіть задану площу на задану основу, щоб знайти відсутню висоту.

    \(25\div 5=5\)

    \(\text{ Height }= 5\: meters\)

    Відповідь - висота - 5 метрів.

    Приклад\(\PageIndex{4}\)

    Знайдіть відсутню розмірність паралелограма за допомогою заданих вимірювань.

    Площа = 81 квадратних футів

    База = 27 футів

    Рішення

    Спочатку розділіть задану площу на задану основу, щоб знайти відсутню висоту.

    \(81\div 27=3\)

    \(\text{ Height }= 3 \text{ feet }\)

    Відповідь - висота - 3 фути.

    Приклад\(\PageIndex{5}\)

    Знайдіть відсутню розмірність паралелограма за допомогою заданих вимірювань.

    Площа = 36 квадратних дюймів

    Висота = 2 дюйми

    Рішення

    Спочатку розділіть задану площу на задану висоту, щоб знайти відсутню основу.

    \(36\div 2=18\)

    \(\text{ Height }= 18\text{ inches }\)

    Відповідь - висота 18 дюймів.

    Рецензія

    Використовуйте задану площу та інший вимір, щоб знайти відсутню основу або висоту.

    1. Площа = 22 кв. дюймів, База = 11 дюймів
    2. Площа = 50 кв. миль, База = 10 миль
    3. Площа = 48 кв. дюймів, База = 8 дюймів
    4. Площа = 30 кв. метрів, Підстава = 15 метрів
    5. Площа = 45 кв. футів, Висота = 3 фути
    6. Площа = 88 кв. футів, Висота = 8 футів
    7. Площа = 121 кв. футів, Висота = 11 футів
    8. Площа = 160 кв. миль, Висота = 20 миль
    9. Площа = 90 кв. метрів, Висота = 30 метрів
    10. Площа = 100 кв. футів, База = 25 футів
    11. Площа = 120 кв. футів, База = 20 футів
    12. Площа = 144 кв. футів, База = 12 футів
    13. Площа = 200 кв. футів, База = 20 футів
    14. Площа = 400 кв. футів, База = 200 футів
    15. Площа = 360 кв. футів, База = 100 футів

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 10.2.

    Лексика

    Термін Визначення
    Площа Площа - це простір в межах периметра двомірної фігури.
    Прямокутник Прямокутник - це чотирикутник з чотирма прямими кутами.

    Додаткові ресурси

    Відео: Площа паралелограма (цілі числа)

    Практика: Невідомі розміри паралелограмів