Skip to main content
LibreTexts - Ukrayinska

5.8: Класифікація паралелограм

  1. Last updated
  2. Save as PDF
  • Page ID
    54861

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Прямокутники, ромби та квадрати - це паралелограми, визначені їх діагоналями, кутами та сторонами.

    Класифікація паралелограмів

    Прямокутники, ромби (їх ще називають ромбами) і квадрати - все це більш специфічні варіанти паралелограмів, які також називають спеціальними паралелограмами.

    • Чотирикутник - це прямокутник тоді і тільки тоді, коли він має чотири правих (конгруентні) кути.
    F-д_55е51 да 65А21709104Д743390Е53Ф091Е33409ФБД0ФБД0ФЕД 707А7Е86160Б+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    \(ABCD\)це прямокутник, якщо і тільки якщо\(\angle A\cong \angle B\cong \angle C\cong \angle D\).

    • Чотирикутник - це ромб тоді і тільки тоді, коли він має чотири конгруентні сторони.
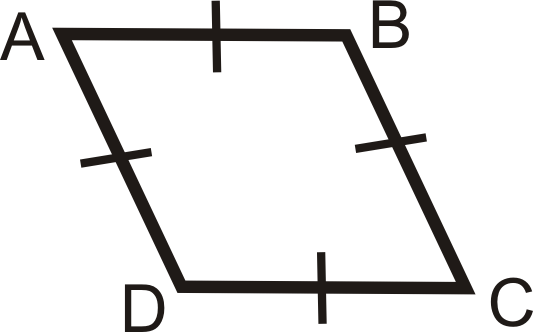
    Ф-Д_БД0Б9С5С9Ф7ЕДФ 9469 Де40А2Д7Д8ФБК 7С07Б51868395123308E+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    \(ABCD\)це ромб, якщо і тільки якщо\(\overline{AB}\cong \overline{BC} \cong \overline{CD} \cong \overline{AD}\).

    • Чотирикутник - це квадрат тоді і тільки тоді, коли він має чотири прямі кути і чотири конгруентні сторони. За визначенням квадрат - це прямокутник і ромб.
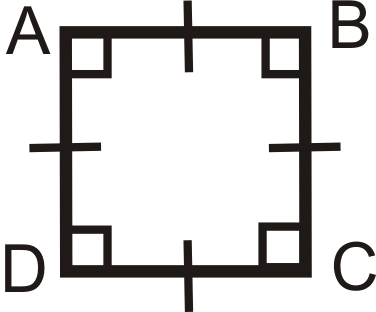
    F-д_117Ф8Д8С3160д46 Бул 944д23340Д5Д3Б2274351 ЕЦБ40Б72ФБК 502384+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    \(ABCD\)квадрат, якщо і тільки якщо\(\angle A\cong \angle B\cong \angle C\cong \angle D\) і\(\overline{AB}\cong \overline{BC} \cong \overline{CD} \cong \overline{AD}\).

    Ви завжди можете показати, що паралелограм - це прямокутник, ромб або квадрат, використовуючи визначення цих фігур. Є кілька додаткових способів довести, що паралелограми є прямокутники і ромби, показані нижче:

    1. Паралелограм - це прямокутник, якщо діагоналі конгруентні.

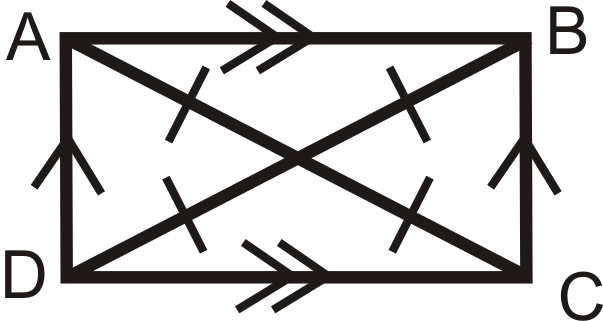
    Ф-д_3ф84б99д 72ЕС3008797 ліжко д 79д89д66А87Д1ФД7604КА 0Ф9 ЕД59Е74+зображення_крихіткий+зображення_крихітка_крихітка_png
    Малюнок\(\PageIndex{4}\)

    \(ABCD\)є паралелограмом. Якщо\(\overline{AC}\cong \overline{BD}\), то\(ABCD\) теж прямокутник.

    2. Паралелограм - це ромб, якщо діагоналі перпендикулярні.

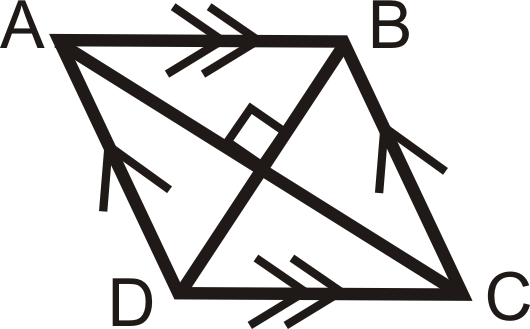
    F-D_226D4522740 ББД 606Е 2Ф9С557Д0А6АЕ 466Ф03А84173C742D6654F998+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    \(ABCD\)є паралелограмом. Якщо\(\overline{AC}\perp \overline{BD}\),\(ABCD\) то ще й ромб.

    3. Паралелограм - це ромб, якщо діагоналі розділяють кожен кут.

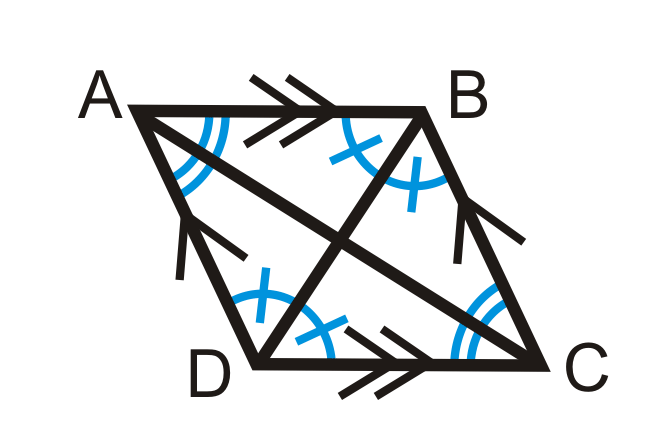
    Ф-д_9Е07С43ЕЦ29Ф52201Е 20ДБ4381 Фе 8 ЕФ 2А2568Б573 КДА3020294030+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    \(ABCD\)є паралелограмом. Якщо\(\overline{AC}\)\(\angle BAD\) бісекції\(\angle BCD\) і\(\angle ABC\) і\(\overline{BD}\)\(\angle ADC\) бісекції і,\(ABCD\) то теж ромб.

    Що робити, якщо вам дали паралелограм і інформацію про його діагоналі? Як ви можете використовувати цю інформацію, щоб класифікувати паралелограм як прямокутник, ромб та/або квадрат?

    Приклад\(\PageIndex{1}\)

    Це прямокутник ІНОДІ, ЗАВЖДИ, або НІКОЛИ не паралелограм? Поясніть чому.

    Рішення

    Прямокутник має два набори паралельних сторін, тому він ЗАВЖДИ є паралелограмом.

    Приклад\(\PageIndex{2}\)

    Чотирикутник ІНОДІ, ЗАВЖДИ або НІКОЛИ не п'ятикутник? Поясніть чому.

    Рішення

    Чотирикутник має чотири сторони, тому він НІКОЛИ не буде п'ятикутником з п'ятьма сторонами.

    Приклад\(\PageIndex{3}\)

    Які типи паралелограма наведені нижче цифри?

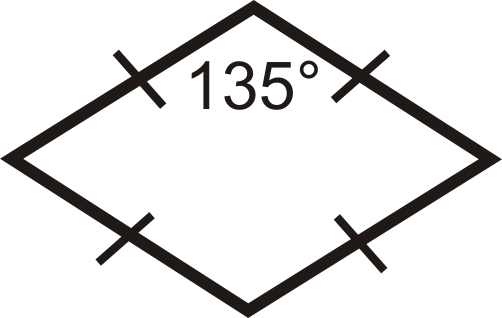
    Ф-д_БАЕФ9Д45СБ8А7СБ 0757766Ф 5ЕБ7896623452809ЕЕ0Д287ЕД 3Ф92CF66+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{7}\)
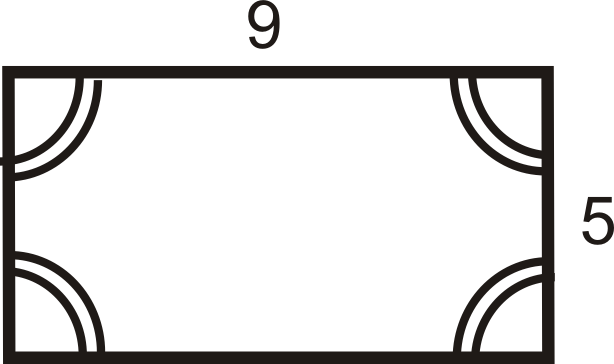
    F-D_19F82E49CCAE 0С33КД1Б41448Б5Д5091 ДК9 ДБ3098Ф54898CF74C2+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{8}\)

    Рішення

    Для першої фігури всі сторони конгруентні і один кут є\(135^{\circ}\), тому кути не конгруентні. Це ромб.

    Для другої фігури всі чотири кути конгруентні, але сторони - ні. Це прямокутник.

    Приклад\(\PageIndex{4}\)

    Ромб ІНОДІ, ЗАВЖДИ або НІКОЛИ не квадрат? Поясніть чому.

    Рішення

    Ромб має чотири конгруентні сторони, а квадрат має чотири конгруентні сторони та кути. Тому ромб - це квадрат, коли він має конгруентні кути. Це означає, що ромб іноді є квадратом.

    Приклад\(\PageIndex{5}\)

    Перерахуйте все, що ви знаєте про квадрат\(SQRE\).

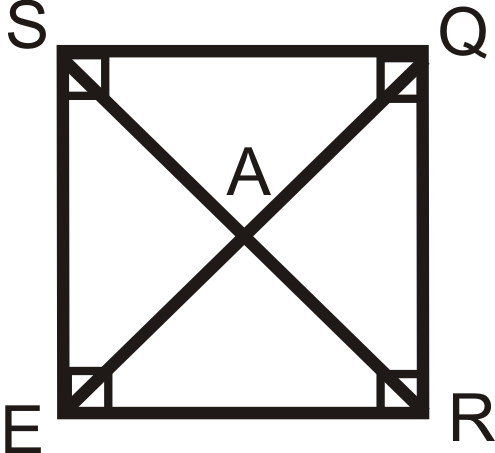
    F-D_51A51 С13C90A76DA7E03AB078819 AEC 1967135978 БК 4Ф децид 2F01C4+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{9}\)

    Рішення

    Квадрат має всі властивості паралелограма, прямокутника і ромба.

    Властивості паралелограма Властивості ромба Властивості прямокутника
    • \(\overline{SQ}\parallel \overline{ER}\)
    • \(\overline{SQ}\cong \overline{ER}\cong \overline{SE}\cong \overline{QR}\)
    • \(m\angle SER=m\angle SQR=m\angle QSE=m\angle QRE=90^{\circ}\)
    • \(\overline{SE}\parallel \overline{QR}\)
    • \(\overline{SR}\perp \overline{QE}\)
    • \(\angle SEQ\cong \angle QER\cong \angle SQE\cong \angle EQR\)
    • \(\overline{SR}\cong \overline{QE}\)
    • \(\angle QSR\cong \angle RSE\cong \angle QRS\cong \angle SRE\)
    • \(\overline{SA}\cong \overline{AR}\cong \overline{QA}\cong \overline{AE}\)

    Всі двосекційні кути є\(45^{\circ}\).

    Рецензія

    1. \(RACE\)являє собою прямокутник. Знайти:
      1. \(RG\)
      2. \(AE\)
      3. \(AC\)
      4. \(EC\)
      5. \(m\angle RAC\)
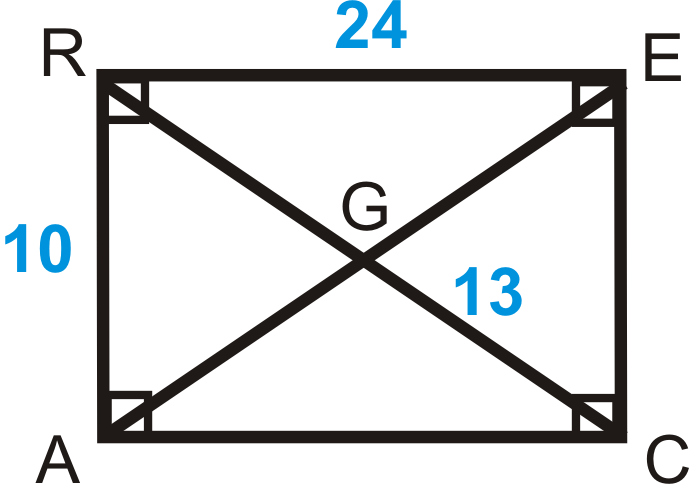      F-D_4329 ЕД 2Б37515С1Б5092 БФ 37 АСЕ63Д2956Е5ЕФС9ФД 9ФД967 АЕФА 280 ФБ+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{10}\)
    2. \(DIAM\)є ромб. Знайти:
      1. \(MA\)
      2. \(MI\)
      3. \(DA\)
      4. \(m\angle DIA\)
      5. \(m\angle MOA\)
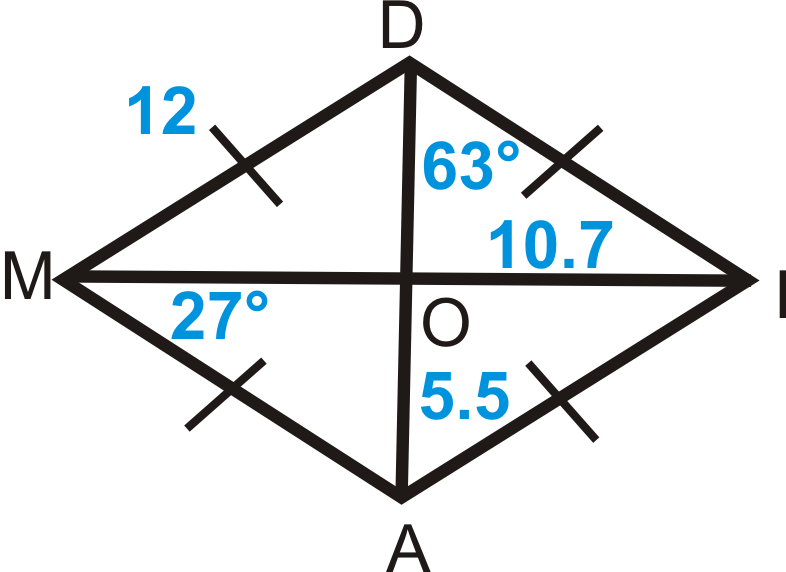      F-д_БА 88 ДК 9166 DA4E8A6D1d9468c026 дек 9d3015a1805f65a74908cde4D+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{11}\)
    3. \(CUBE\)являє собою квадрат. Знайти:
      1. \(m\angle UCE\)
      2. \(m\angle EYB\)
      3. \(m\angle UBY\)
      4. \(m\angle UEB\)
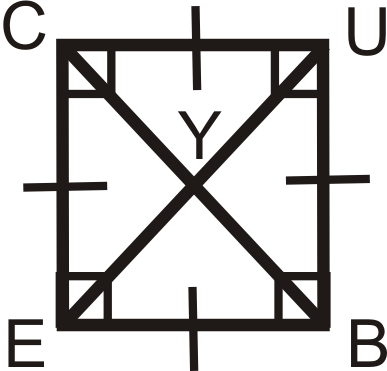
      F-д_3А96А9Б4Е6965 куб.ББФ 65Ф82Ф51Б72109914 Ба6Ф9Ф9А174300С1С8АА+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)

    Для питань 4-15 визначте, чи є чотирикутник паралелограмом, прямокутником, ромбом, квадратом чи ні.

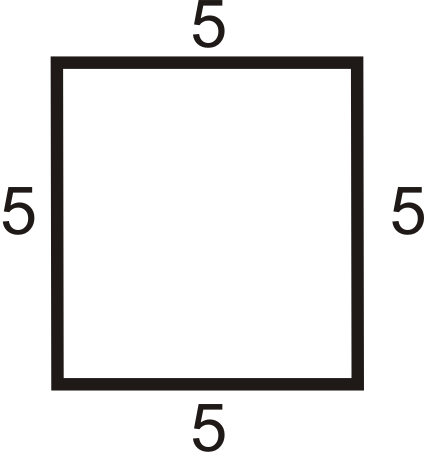
    1. F-д_ЕДФ 879А0303564А5С702961364640Е04А60 АК Ф89Е75А4Ф8А343С+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)
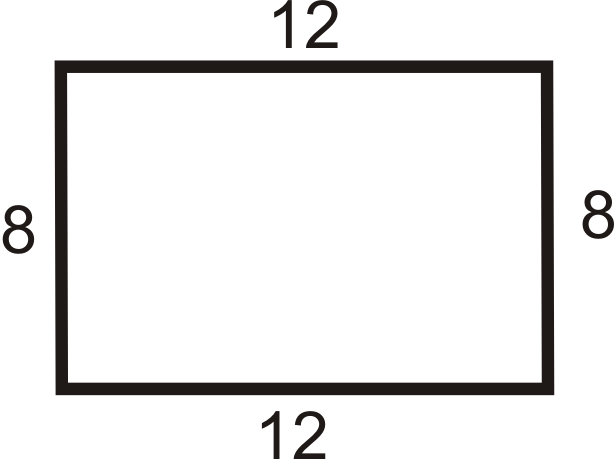
    2. F-д_75310111147d6f01b4375b4003f65512f5827713 АДС560Ф202Б809C5+зображення_крихіткий+зображення_крихіткий_png
      Малюнок\(\PageIndex{14}\)
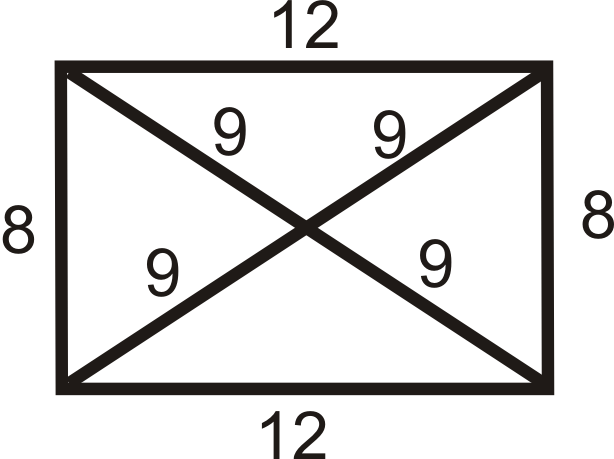
    3. F-D_CD8AEC02A3B ФЕДБФ 82ФА7 АБ7706А4Д87Ф5СЕ06А 06116E6BFFE65D33CB1+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{15}\)
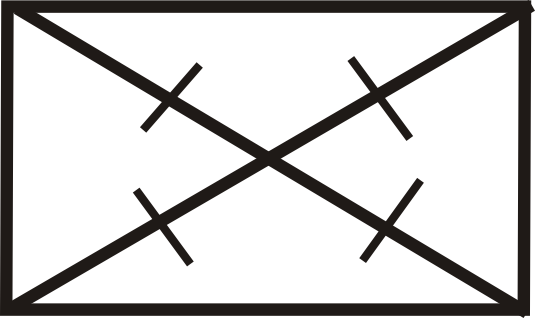
    4. F-д_9Ф77Ф2Е1ДК7Е368А0А0А940 АБ3Б2ЕФ25Ф13Б6А5Б85А07048E0D0CC0БФ+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{16}\)
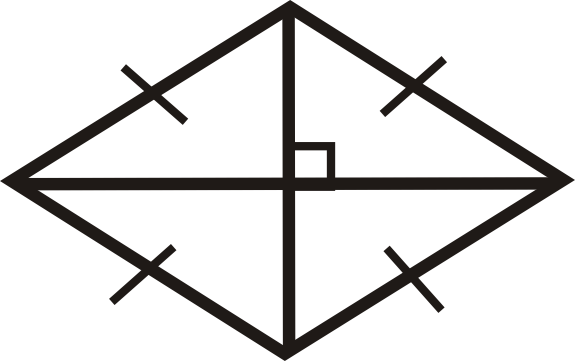
    5. Ф-д_БАФ 0ФФ 29Ф3АФ 261461153Б6005Д955Д58Б46БД277ЕЕ107Е7С+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{17}\)
    6. F-д_22С026132 ЕФК 2729Б47Е751Б89ФБ05Е5704ДА9065ДФД73ФФБ819431+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{18}\)
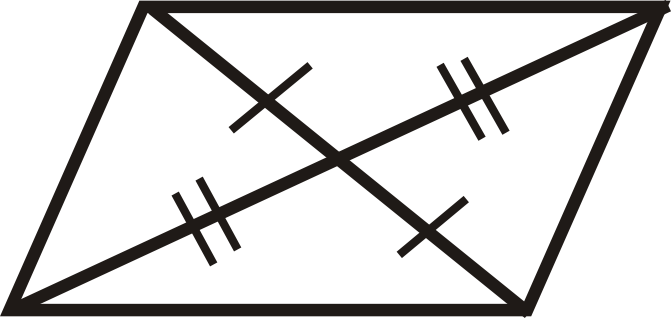
    7. F-D_468C0Ф 4943Б8 CF7Б238А271799А81Б6Е74Ф569027ФБ5Ф61CD39C6569+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{19}\)
    8. F-D_24CF4DE09666DE172DDF99CDA314ЕА 94кд 79532С17БД2038А6ЕФ5Б+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{20}\)
    9. F-д_37д25Е5Е7482С22988Е 6203 БФА4С4411Е4А2Д5Д8Ф2 Деб 8720С2+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{21}\)
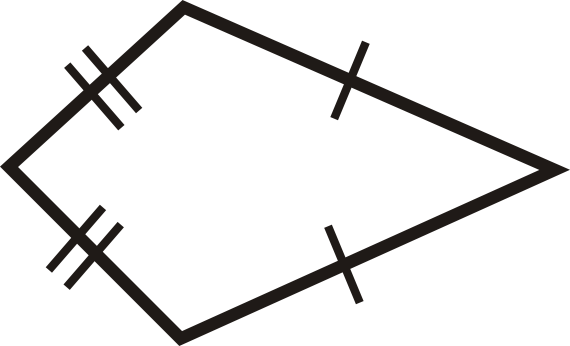
    10. F-д_42c64052c5942C 19464501А150Е629Е9371А976602E14AE858B735F+зображення_крихіткий+зображення_крихіткий_png
      Малюнок\(\PageIndex{22}\)
    11. F-D_7B54067DAC 4С1495 CFC БД0706АД 44С840С577де 994D607973C664859+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{23}\)
    12. F-д_д063Д4Д8А6А6 А6Е 6Е 6654D3 АБ 65781Ф168Ф6Д72736Ф8Е7716819+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{24}\)

    Для питань 16-19 визначте, чи завжди, колись чи ніколи не відповідають дійсності наступне. Поясніть свої міркування.

    1. Прямокутник - це ромб.
    2. Квадрат - це паралелограм.
    3. Паралелограм регулярний.
    4. Квадрат - це прямокутник.

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 6.5.

    Лексика

    Термін Визначення
    прямокутник Паралелограм - це прямокутник тоді і лише тоді, коли він має чотири правих (конгруентні) кути
    ромб Паралелограм - це ромб тоді і тільки тоді, коли він має чотири конгруентні сторони
    квадрат Паралелограм - це квадрат тоді і тільки тоді, коли він має чотири прямі кути і чотири конгруентні сторони.
    зворотний Якщо умовний оператор є\(p\rightarrow q\) (\(p\)if, то\(q\)), то зворотним є\(q\rightarrow p\) (if\(q\), то\(p\). Зауважте, що зворотне твердження не відповідає дійсності лише тому, що оригінальне твердження є істинним.
    Паралелограм Паралелограм - це чотирикутник з двома парами паралельних сторін.
    Рефлексивне властивість конгруентності \(\overline{AB}\cong \overline{AB}\)або\(\angle B\cong \angle B\)

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Принципи класифікації паралелограм - основні

    Діяльність: Класифікація паралелограм Питання обговорення

    Навчальні посібники: паралелограми навчальний посібник

    Практика: Класифікація паралелограм

    Реальний світ: Паралелограми