5.5: Площа квадратів і прямокутників

Last updated
Save as PDF

Page ID: 54836

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Знайдіть площу квадратів і прямокутників за формулами: базовий раз висотою і стороною в квадраті.

Аллен купив новий будинок і планує замінити килим в двох спальнях. Одна спальня має форму квадрата, а інша - прямокутної. Йому потрібно розібратися, скільки потрібно килима, щоб покрити обидві підлоги спальні.

Квадратна спальня має довжину сторін 9 футів.

F-D_ЕД 2531Б6Ф 35401С5Ф0Ф0Д2 АФ 78734974 АДЕЦ1Е8Д 798416ДК205ФД18+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

Прямокутна спальня має довжину 12 футів і ширину 8 футів.

F-д_34е518Д753Ф89276С232Д9ФДБ22Ф31СА5Е9ББ4ДД3285де31Д1Д6АФ8+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{3}\)

Для того щоб Аллен зрозумів, скільки килима йому потрібно купити для цих двох спалень, йому необхідно знайти площу кожної спальні.

У цій концепції ви дізнаєтеся, як знайти площу квадратів і прямокутників.

Площа

Внутрішній простір фігури відомий як площа фігури. Килимові покриття підлоги, трава на землі, або що-небудь інше, що охоплює простір всередині фігури - все це приклади області.

Існує формула знаходження площі різної форми. У цій концепції це поняття покаже вам, як знайти площу як квадратів, так і прямокутників.

Це формула, яка використовується для знаходження площі квадрата:

\(A=s\cdot s\)

Ф-Д_С8175Д38С7А3С58Ф0А2С5де 2А4Б5622 ББ 3237C0ACE 92BE48F313135+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{4}\)

Пам'ятайте, точка - це ще один символ множення. Щоб з'ясувати площу квадрата, помножте одну сторону на іншу сторону. Оскільки всі сторони в квадраті рівні, два числа будуть однаковими. Одиниця виміру зберігається в рівнянні, щоб допомогти вам запам'ятати, якою має бути правильна мітка.

Ось як використовувати формулу знаходження площі квадрата:

\(A=6\text{ ft }\cdot 6\text{ ft }\)

Тепер подумайте про рівняння як множення двох різних речей; числа та одиниць виміру.

\(A=6\cdot 6\)

\(A=ft\cdot\text{ ft }\)

Вирішити обидва рівняння.

\(A=6\times 6=36\)

\(A=ft\times\text{ ft }=ft^2\)

Подумайте про те, що ви знаєте про експоненти. Коли ви множите два однакових речі разом, ви можете записати це в експоненціальній формі. Інший спосіб позначення площі - написати квадратні фути (кв. фути).

Відповідь -\(36\: sq.\:\text{ ft }.\) чи\(36\:\text{ ft }^2\)

Це формула, яка використовується для пошуку площі прямокутника:

\(A=lw\)

Щоб знайти площу прямокутника, використовуйте вимірювання довжини і ширини замість довжини сторони. Ці числа можуть відрізнятися один від одного, оскільки не всі прямокутники мають однакову довжину сторін, як квадрати.

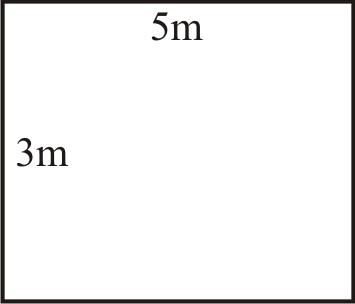
Цей прямокутник вимірює довжину 5 метрів і ширину 3 метри. Так само, як і формула площі для квадрата, помножте ці два числа, щоб знайти площу прямокутника. Пам'ятайте, що дві змінні поруч один з одним у рівнянні вказують на множення, так само, як символ точки або традиційний символ множення. Символи будуть використовуватися як взаємозамінні.

Щоб знайти площу прямокутника, помножте довжину на ширину.

\(A=5\text{ m }\cdot 3\text{ m }\)

\(A=5\times 3\)

\(A=meters\times meters\)

Формула показує 5 метрів на 3 метри. Помножте вимірювальну частину (\(5 \times 3\)), потім помножте одиниці виміру.

Відповідь -\(15\text{ sq. m }\) або\(15 \text{ m}^2\).

Мітка для площі прямокутника схожа на мітку для площі квадрата зверху. Мітка може бути написана в експоненціальній формі або написана абревіатурою.

Приклад\(\PageIndex{1}\)

Раніше вам дали проблему щодо Аллена та його нового будинку, який він хоче повторно килимувати.

Розміри двох спалень Аллена наведені на початку концепції. Його квадратна спальня має довжину сторін 9 футів. Інша кімната являє собою прямокутник з розмірами 12 футів на 8 футів. Щоб почати вирішення цієї проблеми, знайдіть площу кожної зі спалень.

Рішення

Квадратна спальня має довжину сторони 9 футів.

\(A=s\cdot s\)

\(A=9\times 9=81\text{ sq. feet }\)

Квадратна спальня має площу 81 квадратних футів.

Прямокутна спальня має довжину 12 футів і ширину 8 футів.

\(A=12\:\text{ ft }\cdot 8\:\text{ ft }\)

\(A=12\times 8\)

\(A=feet\times feet\)

Прямокутна спальня має площу 96 квадратних футів.

Аллен хоче, щоб загальна площа його двох спалень знала, скільки килима купити, тому додайте дві області разом.

\(81+96=177\text{ square feet }\)

Відповідь - 177 квадратних футів.

Приклад\(\PageIndex{2}\)

Знайдіть площу прямокутника довжиною 7\ text {ft}. і шириною 4\ text {ft}.

Рішення

Спочатку випишіть рівняння

\(A=lw\)

\(A=7\:\text{ ft }\cdot 4\:\text{ ft }\)

Далі множимо два числа.

\(A=7\cdot 4=28\)

Потім помножте одиниці виміру.

\(A=\text{ ft }\cdot\text{ ft }=\text{ ft}^2 \)

Тепер складіть свою відповідь разом, щоб показати остаточне рішення.

\(A=28\text{ ft }^2\)

Відповідь є\(28\: sq.\:\text{ ft }\).

Після того, як ви зробите більше прикладів, ви можете виявити, що пропустили крок множення одиниць виміру. Це може стати природним для квадратної одиниці виміру для будь-якої проблеми площі.

Приклад\(\PageIndex{3}\)

Знайдіть площу квадрата з довжиною сторін 10 дюймів.

Рішення

Спочатку напишіть своє рівняння.

\(A=s\cdot s\)

\(A=10 \text{ in }\cdot 10 \text{ in}\)

Далі вирішуємо рівняння, перемноживши дві довжини сторін.

\( A=10\cdot 10=100\)

Потім напишіть своє остаточне рішення. Не забудьте записати квадратну одиницю виміру після числової відповіді.

\(A=100\text{ in}^2\)

Відповідь - 100 кв.

Приклад\(\PageIndex{4}\)

Знайдіть площу прямокутника довжиною 6 футів і шириною 5 футів.

Рішення

Спочатку напишіть своє рівняння.

\(A=lw\)

\(A=6\:\text{ ft }\cdot 5\:\text{ ft }\)

Далі вирішуємо рівняння, перемноживши довжину на ширину.

\(A=6\cdot 5=30\)

\( A=30\:\text{ ft }^2\)

Відповідь - 30 кв. \ текст {ft}.

Приклад\(\PageIndex{5}\)

Знайдіть площу прямокутника довжиною 9 метрів і шириною 8 метрів.

Рішення

Спочатку напишіть своє рівняння.

\(A=lw\)

\(A=9\text{ m }\cdot 8\text{ m }\)

Далі вирішуємо рівняння, перемноживши довжину на ширину.

\(A=9\cdot 8=72\)

\(A=72\text{ m }^2\)

Відповідь - 72 кв. м

Рецензія

Знайдіть площу кожної з наступних фігур. Переконайтеся, що ви правильно позначили свою відповідь.

Квадрат з довжиною сторони 6 дюймів.
Квадрат з довжиною сторони 4 дюйми.
Квадрат з довжиною сторони 8 сантиметрів.
Квадрат з довжиною сторони 12 сантиметрів.
Квадрат з довжиною сторони 9 метрів.
Прямокутник довжиною 6 дюймів і шириною 4 дюйми.
Прямокутник довжиною 9 метрів і шириною 3 метри.
Прямокутник довжиною 4 метри і шириною 2 метри.
Прямокутник довжиною 17 футів і шириною 12 футів.
Прямокутник довжиною 22 фути і шириною 18 футів.
Квадрат з довжиною сторони 13 футів.
Квадрат з довжиною сторони 18 футів.
Квадрат з довжиною сторони 21 фут.
Прямокутник довжиною 18 футів і шириною 13 футів.
Прямокутник довжиною 60 футів і шириною 27 футів.
Прямокутник довжиною 57 футів і шириною 22 фути.

Ресурси

Додатковий ресурс

Відео: Визначаємо площу прямокутника за участю цілих чисел

Практика: Площа квадратів і прямокутників