Skip to main content
LibreTexts - Ukrayinska

4.16: ГЛ

  1. Last updated
  2. Save as PDF
  • Page ID
    54740

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Конгруентність трикутника HL

    Теорема про конгруентність гіпотенузи-ноги

    Якщо гіпотенуза і катет в одному прямокутному трикутнику конгруентні гіпотенузі і катета в іншому прямокутному трикутнику, то два трикутника конгруентні. Це називається теоремою конгруентності гіпотенузи-ноги (HL). Зверніть увагу, що він буде працювати тільки для прямих трикутників.

    Якщо\(\Delta ABC\) і\(\Delta XYZ\) обидва правильні трикутники\(\overline{AB}\cong \overline{XY}\) і\(\overline{BC}\cong \overline{YZ}\) то\(\Delta ABC\cong \Delta XYZ\).

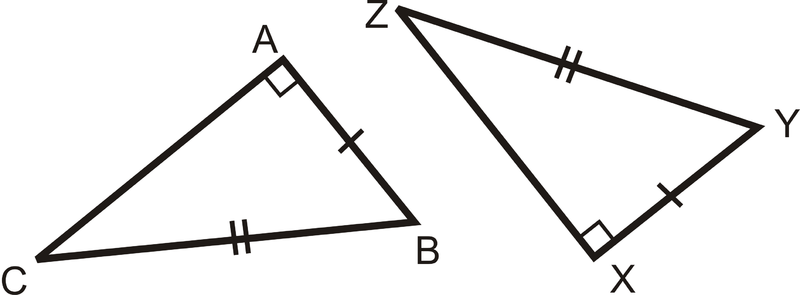
    F-D_BDC 5925739D692062 Ед д 37132ед д 5дФ Ф 4 д59С6930БК9968664 CF3A64+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Що робити, якщо вам дали два правильних трикутника і забезпечили лише мірою їх гіпотенусів і одного з їхніх катетів? Як ви могли визначити, чи два правильні трикутники були конгруентними?

    Приклад\(\PageIndex{1}\)

    Заповніть пропуски в доказі нижче.

    Дано:

    \(\overline{SV}\perp \overline{WU}\)

    \(T\)є середньою точкою\(\overline{SV}\) і\(\overline{WU}\)

    Доведіть:\(\overline{WS}\cong \overline{UV}\)

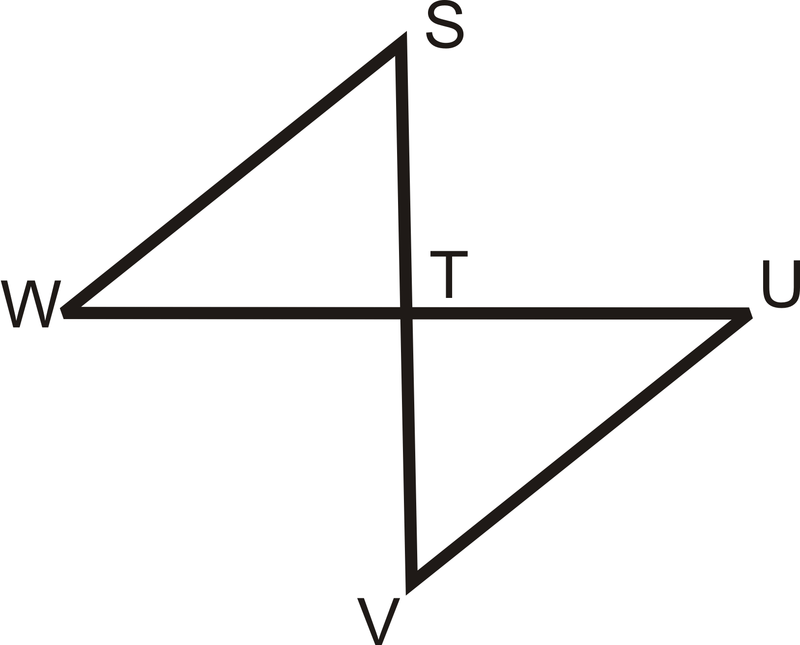
    F-д_ДФК 4651д79ЕФ4А542С0Ф274Д7ДДБ920Б7Б554808478А778Б4350ФБ9+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Рішення

    Заява Причина
    1. 1.
    2. \(\angle STW\)і\(\angle UTV\) є прямими кутами 2.
    3. 3.
    4. \(\overline{ST}\cong \overline{TV}\),\(\overline{WT}\cong \overline{TU}\) 4.
    5. \(\Delta STW\cong \Delta UTV\) 5.
    6. \(\overline{WS}\cong \overline{UV}\) 6.
    Заява Причина
    1. \(\overline{SV}\perp \overline{WU}\) 1. Враховується
    2. \(\angle STW\)і\(\angle UTV\) є прямими кутами 2. Визначення перпендикулярних ліній.
    3. \(T\)є середньою точкою\(\overline{SV}\) і\(\overline{WU}\) 3. Враховується
    4. \(\overline{ST}\cong \overline{TV}\),\(\overline{WT}\cong \overline{TU}\) 4. Визначення середньої точки
    5. \(\Delta STW\cong \Delta UTV\) 5. САС
    6. \(\overline{WS}\cong \overline{UV}\) 6. CPCTC

    Зверніть увагу, що хоча це були правильні трикутники, ми не використовували ярлик конгруентності HL, тому що ми спочатку не дали, що дві гіпотенуси були конгруентними. У цьому випадку ярлик конгруентності SAS був швидшим.

    Приклад\(\PageIndex{2}\)

    Поясніть, чому працює ярлик HL Congruence.

    Теорема Піфагора, яка говорить, що для будь-якого прямокутного трикутника це рівняння вірно:

    \((leg)^2+(leg)^2=(hypotenuse)^2\)

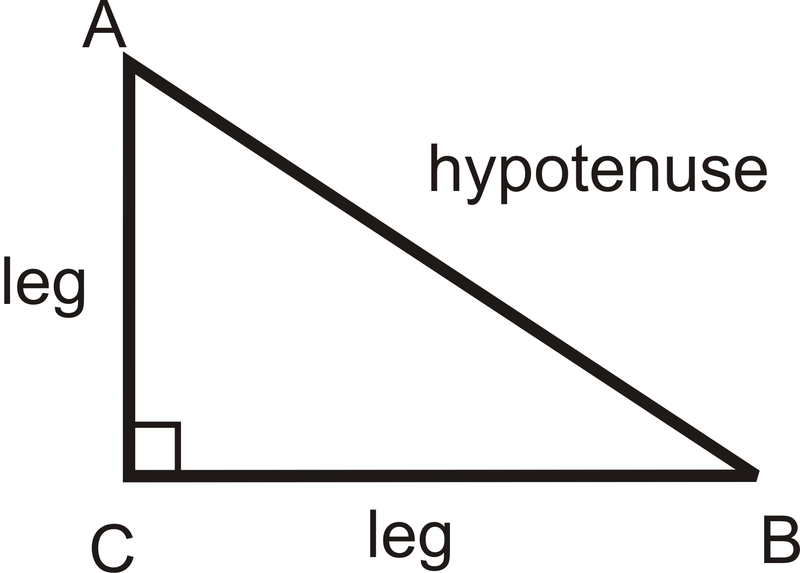
    F-D_028895 ЕФСБ5 ЕББ 615 ФФА1 СД 592А5674 Д7Д2603А1Б71С4E5645F+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Рішення

    Це означає, що якщо вам дано дві сторони прямокутного трикутника, ви завжди можете знайти третю. Тому, якщо ви знаєте, що дві сторони прямокутного трикутника конгруентні двом сторонам іншого прямокутного трикутника, то можна зробити висновок, що треті сторони також є конгруентними. Якщо три пари сторін конгруентні, то ми знаємо, що трикутники конгруентні по ССС.

    Приклад\(\PageIndex{3}\)

    Яка додаткова інформація вам потрібна, щоб довести, що ці два трикутники були конгруентними, використовуючи теорему HL?

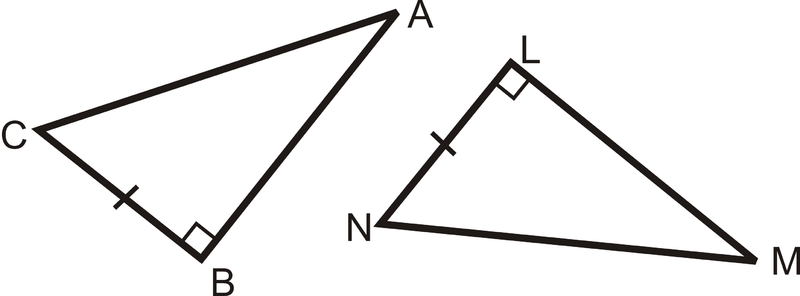
    F-д_2Е4Е 38Д83ЕФ1ЕБ0752784 Ад 7822949 АД 301d9689 ЕФ3А2КС647DF6D+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Рішення

    Для HL потрібно, щоб гіпотенуси були конгруентними. \(\overline{AC}\cong MN\overline{AB}\).

    Приклад\(\PageIndex{4}\)

    Визначте, чи конгруентні трикутники. Якщо вони є, напишіть заяву про конгруентність і який постулат конгруентності або теорему ви використовували.

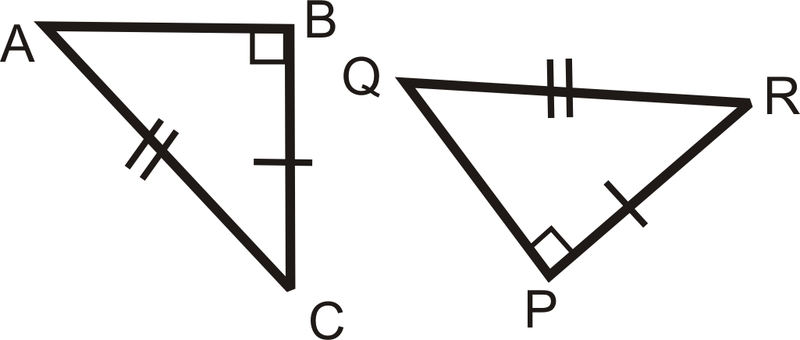
    F-д_Ф11С7С9Д8Д33Б901Е5БФДБК82С00Е11047Ф93130Б1БД18А5E4217757+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Рішення

    Ми знаємо, що два трикутники є прямими трикутниками. Мають одну пару катетів, яка є конгруентною, і їх гіпотенуси є конгруентними. Це означає, що\(\Delta ABC\cong \Delta RQP\) по HL.

    Приклад\(\PageIndex{5}\)

    Визначте додаткову інформацію, необхідну для того, щоб показати, що два трикутники є конгруентними по HL.

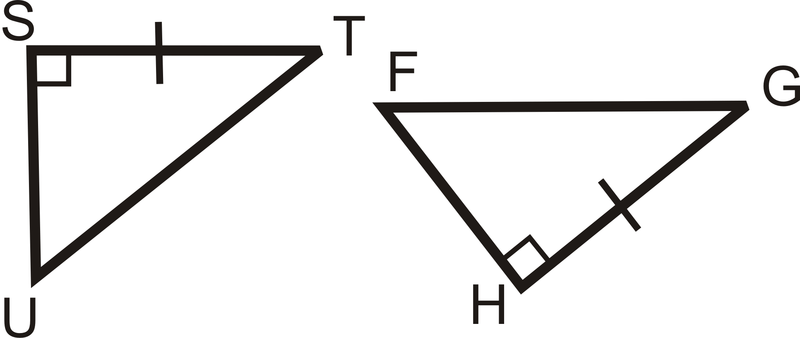
    Ф-д_С249Д6Е60253С635С1Е1А99101Е70128ЕД 80AA01E3155D0465F96F6+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    Рішення

    Ми вже знаємо, що одна пара ніг є конгруентною і що вони є прямими трикутниками. Додаткова інформація, яка нам потрібна, полягає в тому, що дві гіпотенуси є конгруентними,\(\overline{UT}\cong \overline{FG}\).

    Рецензія

    Використовуючи теорему HL, яка додаткова інформація вам потрібна, щоб довести, що два трикутники є конгруентними?


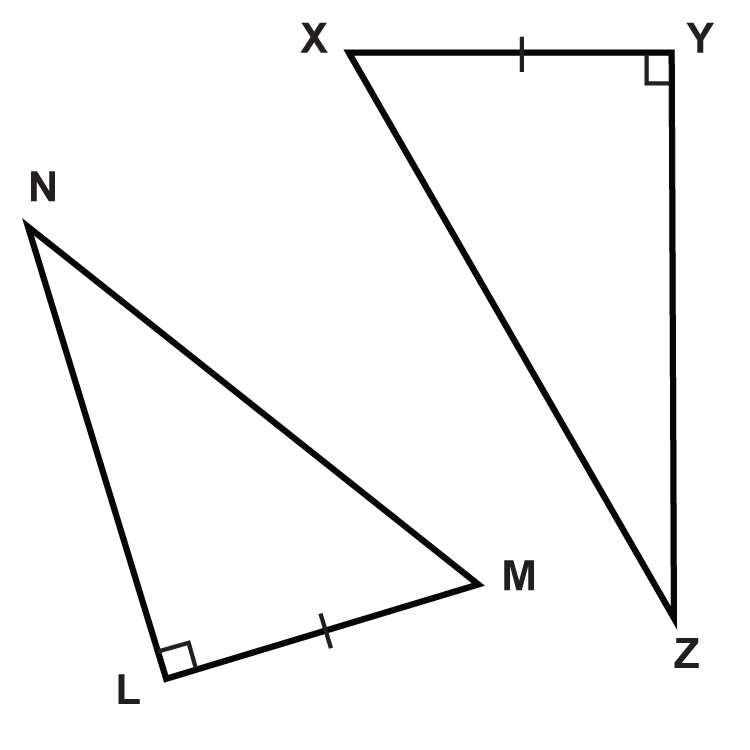
    1. F-д_51ФКК 0739Е 776784d648E1БК 7д7992ФД88Е0Д408С9С329Б3C0044790+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{7}\)
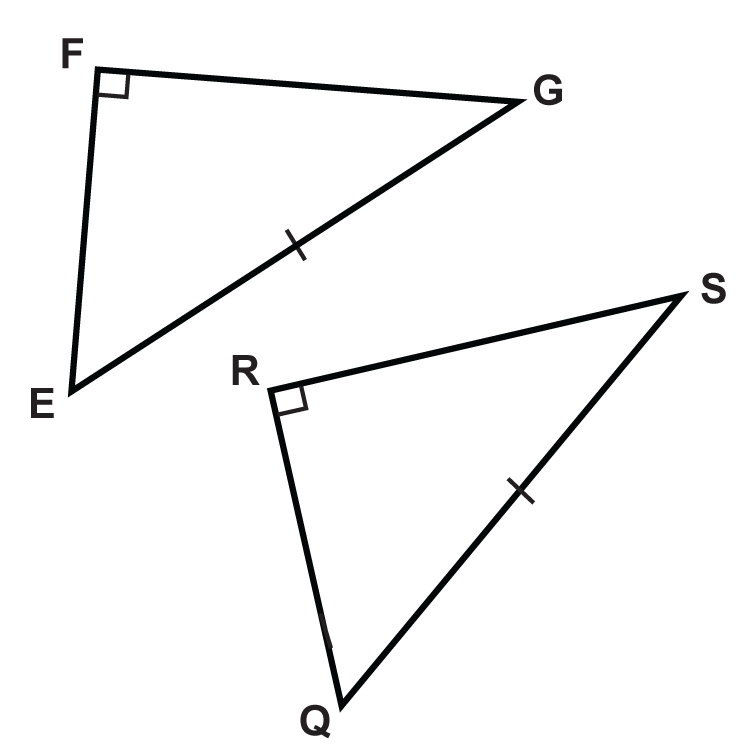
    2. F-D_48C CAE 309C888E9A32C019D8D81688 ДБ35А7Ф8237Ф322C9E5E138F7AE+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{8}\)
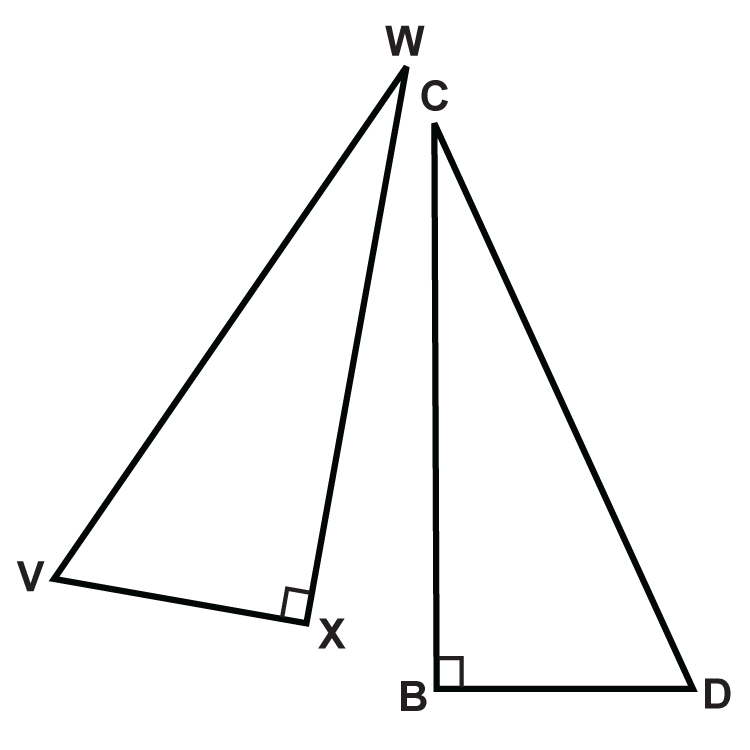
    3. F-д_д69409 А49Д4А1Б9С803392 ЕДДД4Д8236А3С73328Б6Б3Б3Б3Б40ДФ+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{9}\)

    Трикутники утворені двома паралельними лініями, розрізаними перпендикулярним поперечним. \(C\)є середньою точкою\(\overline{AD}\). Заповніть доказ, щоб показати, що два трикутники є конгруентними. Питання 4-7 знаходяться в межах доказування.

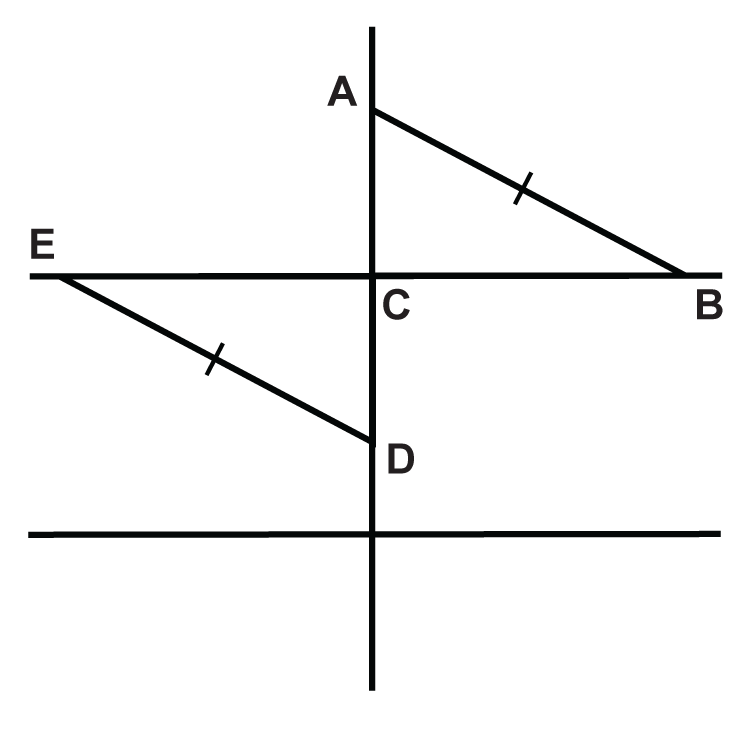
    Ф-д_6119202С08336 АФ 36136451261855Б86Б11С43ДБ 5158А51Б23Б6ДФ+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{10}\)
    Заява Причина
    1. \(\angle ACB\)і\(\angle DCE\) є прямими кутами. (4.)
    2. (5.) Визначення середньої точки
    3. (6.) Враховується
    4. \(\Delta ACD\cong \Delta DCE\) (7.)

    Виходячи з наступних деталей, чи є два правильні трикутники остаточно конгруентними? Заяви не будуються один від одного.

    1. Гіпотенузи двох прямих трикутників конгруентні.
    2. Обидва набори ніг у двох правильних трикутників є конгруентними.
    3. Один набір ніжок конгруентні в двох правильних трикутниках.
    4. Гіпотенузи і одна пара катетів конгруентні в двох прямих трикутниках.
    5. Один з не прямих кутів двох правильних трикутників є конгруентним.
    6. Всі кути двох прямих трикутників є конгруентними.
    7. Всі сторони двох правильних трикутників конгруентні.
    8. Обидва трикутника мають одну ніжку, яка вдвічі перевищує довжину іншої.

    Ресурси

    Лексика

    Термін Визначення
    гіпотенуза Сторона, протилежна прямому куту в прямокутний трикутник.
    ніжки Дві сторони примикають до прямого кута.
    прямокутний трикутник Трикутник з рівно одним прямим (\(90^{\circ}\)) кутом. Дві сторони, прилеглі до прямого кута, називаються катетами, а сторона, протилежна прямому куту, називається гіпотенузою.
    Теорема конгруентності H-L (гіпотенузи-ніжка) Якщо гіпотенуза і катет в одному прямокутному трикутнику конгруентні гіпотенузі і катета в іншому прямокутному трикутнику, то два трикутника конгруентні.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Принципи конгруентності трикутника HL - Основні

    Діяльність: HL Трикутник Конгруентність обговорення Питання

    Навчальні посібники: Посібник з вивчення конгруентності три

    Практика: HL

    Реальний світ: фінальні чернетки