4.2: Класифікуйте трикутники за допомогою вимірювання кута

Визначте трикутники як гострі, правильні, тупі або рівнокутні.

Класифікація трикутників за кутами

Малюнок$\PageIndex{1}$

Мати Михайла купила кедді, який поміщається в кутку. Вона використовує кедді для зберігання своїх віників і швабр в гаражі. Мамина кедді мала вигляд прямокутного трикутника при погляді зверху і ідеально вписувалася в кут. Майклу сподобався кедді, але він не міг дозволити собі придбати такий, як її, тому він вирішив зробити свій власний. Він купив дерево і цвяхи і зібрав їх разом, але коли він спробував поставити його в кутку в своїй кімнаті, він не помістився. Він вимірює кути свого кедді і розуміє, що верх - це трикутник нижче:

Малюнок$\PageIndex{2}$

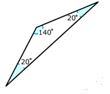
Яка класифікація Михайлівського трикутника?

У цій концепції ви дізнаєтеся, як використовувати кути для класифікації трикутників.

Класифікація трикутників за кутами

Приставка «три» означає три. Трикутник означає три кута.

Щоб класифікувати трикутник за його кутами, необхідно дивитися на кути всередині трикутника. Використовуйте кількість градусів в цих кутах, щоб класифікувати трикутник. Давайте подивимося на картинку трикутника, щоб пояснити.

Малюнок$\PageIndex{3}$

Подивіться на міру кожного кута всередині трикутника, щоб зрозуміти, що це за трикутник. Існує чотири типи трикутників на основі кутових вимірювань.

Прямокутний трикутник - це трикутник, який має один прямий кут і два гострих кута. Один з кутів у трикутнику вимірює,$90^{\circ}$ а інші два кути менше 90. Ось картинка прямокутного трикутника.

Малюнок$\PageIndex{4}$

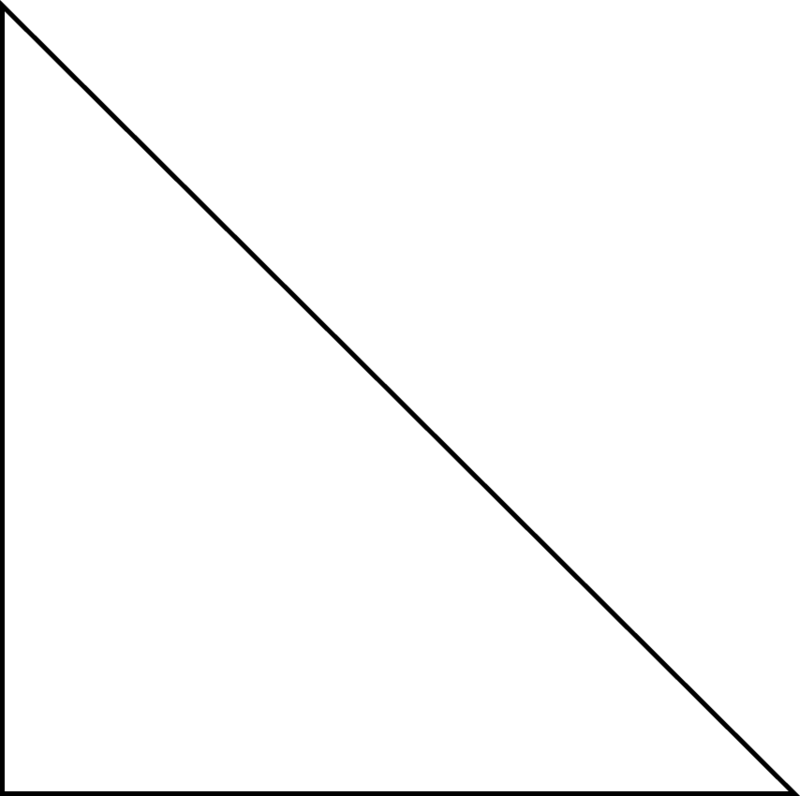
Ви можете бачити, що кут 90 градусів - це той, що знаходиться в нижньому лівому куті. Ви навіть можете малювати в маленькій коробці, щоб визначити його як кут 90 градусів. Якщо ви подивитеся на інші два кути, ви можете побачити, що ці кути менше 90 градусів і є гострими.

Давайте розглянемо приклад прямого кута.

Малюнок$\PageIndex{5}$

його трикутник має один$90^{\circ}$ кут і два$45^{\circ}$ кути. Знайдіть суму трьох кутів.

$90+45+45=180^{\circ}$

Сума трьох кутів трикутника завжди дорівнює$180^{\circ}$.

У рівнокутному трикутнику всі три кути рівні.

Малюнок$\PageIndex{6}$

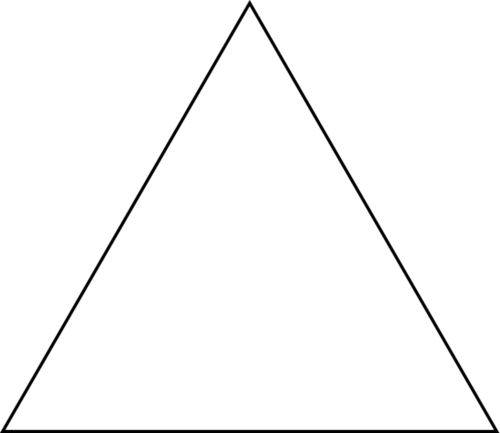
Три кута цього трикутника рівні. Це рівнокутний трикутник.

Ви знаєте, що сума трьох кутів дорівнює$180^{\circ}$, тому, щоб всі три кути були рівними, кожен кут повинен дорівнювати$60^{\circ}$.

$60+60+60=180^{\circ}$

Сума кутів дорівнює$180^{\circ}$.

У гострому трикутнику всі три кути трикутника менше 90 градусів. Ось приклад гострого трикутника.

Малюнок$\PageIndex{7}$

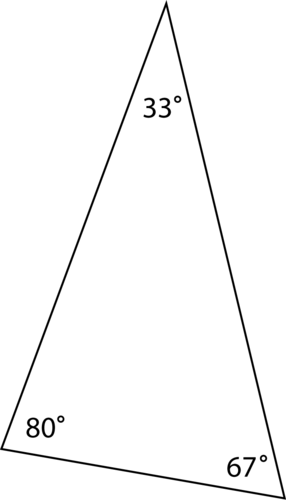
Всі три з цих кутів вимірюють менше 90 градусів.

$33+80+67=180^{\circ}$

Сума кутів дорівнює$180^{\circ}$.

Тупий трикутник має один кут, який більше 90, і два кути, які менше 90.

Малюнок$\PageIndex{8}$

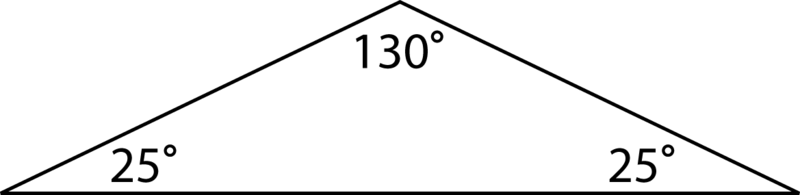
$130+25+25=180^{\circ}$

Сума кутів дорівнює$180^{\circ}$.

Приклад$\PageIndex{1}$

Раніше вам давали проблему про Майкла і його кедді.

Він намагався побудувати кедді, як кедді матері. Її кедді виглядав як прямокутний трикутник зверху, але він закінчив будувати той, який мав такі заходи та зовнішній вигляд зверху:

Малюнок$\PageIndex{9}$

Рішення

Яка класифікація Михайлівського трикутника?

Спочатку перерахуйте заходи кута.

20, 20, 140

Далі визначте, чи рівний будь-який з кутів 90 градусів або більше 90 градусів.

Так, один кут більше 90 градусів

Потім класифікуйте трикутник.

тупого

Відповідь - тупий трикутник. Майкл створив тупий трикутник замість прямокутного трикутника.

Приклад$\PageIndex{2}$

Визначте тип трикутника відповідно до його кутів.

Малюнок$\PageIndex{10}$

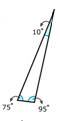
Рішення

Спочатку перерахуйте заходи кута.

10, 75, 95

Далі визначте, чи рівний будь-який з кутів 90 градусів або більше 90 градусів.

Так, один кут більше 90 градусів

Потім класифікуйте трикутник.

тупого

Відповідь - тупий трикутник.

Приклад$\PageIndex{3}$

Визначте тип трикутника відповідно до його кутів.

Малюнок$\PageIndex{11}$

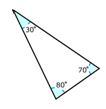
Рішення

Спочатку перерахуйте заходи кута.

30, 70 і 80

Далі визначте, чи рівний будь-який з кутів 90 градусів або більше 90 градусів.

Ні

Потім класифікують кут.

Гострий

Відповідь - гострий трикутник.

Приклад$\PageIndex{}$

Визначте тип трикутника відповідно до його кутів.

Малюнок$\PageIndex{12}$

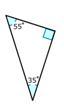
Рішення

Спочатку перерахуйте заходи кута.

35, 55 і 90

Далі визначте, чи рівний будь-який з кутів 90 градусів або більше 90 градусів.

Так, один з кутів дорівнює 90 градусам

Потім класифікують кут.

Правий

Відповідь - прямокутний трикутник

Приклад$\PageIndex{5}$

Класифікуйте трикутник, дивлячись на суму його кутів.

$40^{\circ}+60^{\circ}+80^{\circ}=180^{\circ}$

Рішення

Спочатку перерахуйте заходи кута.

40, 60 і 80

Далі визначте, чи рівний будь-який з кутів 90 градусів або більше 90 градусів.

Ні

Потім класифікують кут.

Гострий

Відповідь - гострий трикутник.

Рецензія

Класифікуйте кожен трикутник відповідно до його кутів.

1. 

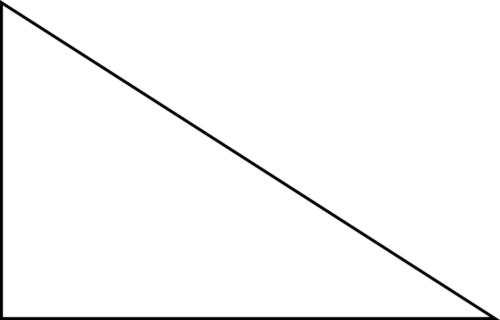
   Малюнок$\PageIndex{13}$

2. 

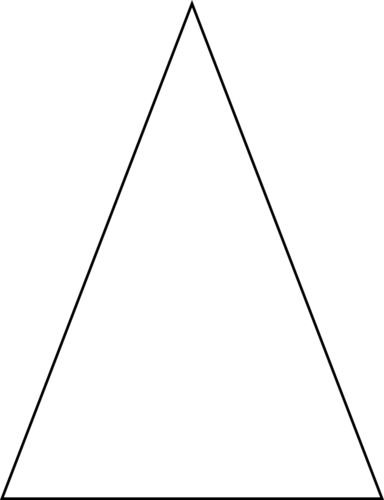
   Малюнок$\PageIndex{14}$

3. 

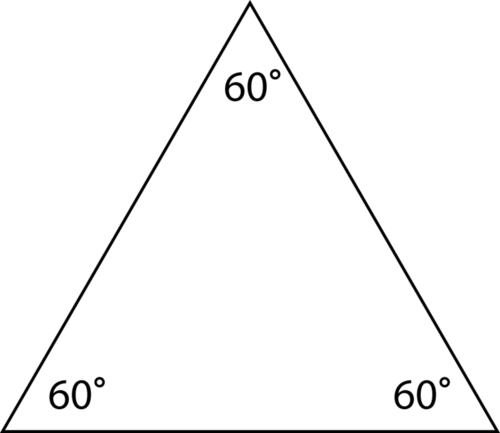
   Малюнок$\PageIndex{15}$

4. 

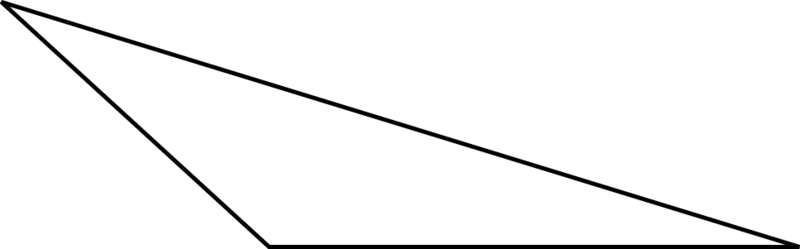
   Малюнок$\PageIndex{16}$

5. 

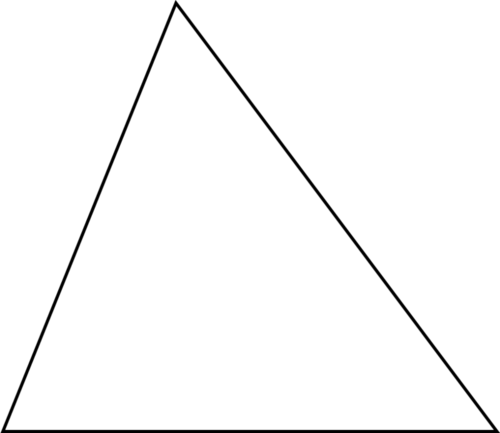
   Малюнок$\PageIndex{17}$

Класифікуйте наступні трикутники, дивлячись на суму мір кута.

6. $40+55+45=180^{\circ}$
7. $20+135+25=180^{\circ}$
8. $30+90+60=180^{\circ}$
9. $60+60+60=180^{\circ}$
10. $110+15+55=180^{\circ}$
11. $105+65+10=180^{\circ}$
12. $80+55+45=180^{\circ}$
13. $70+45+65=180^{\circ}$
14. $145+20+15=180^{\circ}$
15. $60+80+40=180^{\circ}$

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 9.7.

Ресурси

Лексика

Термін	Визначення
Гострий трикутник	Гострий трикутник має три кути, кожен з яких вимірює менше 90 градусів.
Рівносторонній трикутник	Рівносторонній трикутник - це трикутник, у якого всі три сторони мають однакову довжину.
Тупий трикутник	Тупий трикутник - це трикутник з одним кутом, який більше 90 градусів.
Правий трикутник	Прямокутний трикутник - це трикутник з одним кутом 90 градусів.
Трикутник	Трикутник - це багатокутник з трьома сторонами і трьома кутами.

Додатковий ресурс

Інтерактивний елемент

Відео: Кутові відносини і типи трикутників

Практика: Класифікуйте трикутники за допомогою вимірювання кута