Skip to main content
LibreTexts - Ukrayinska

1.16: Відсутні заходи взаємодоповнюючих та додаткових кутів

  1. Last updated
  2. Save as PDF
  • Page ID
    54936

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Знайдіть відсутні кутові заходи для додаткових або додаткових кутів.

    Давайте подумаємо про це

    F-D_9C82Б3БК22Б8Ф7ДБ0Ф05CB953753E329508БК6Ф17242363742E1250+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_jpgМалюнок\(\PageIndex{1}\)

    Марко будує будинок. Він купив багато дерева, щоб зробити каркас будинку. Він хоче прямих кутів для своїх кутів. Якщо він використовує шматок дерева, який вирізається\(55^{\circ}\) під кутом, якою має бути міра кута іншого шматка дерева, який він використовує для завершення кута?

    У цій концепції ви дізнаєтеся, як міркування можуть допомогти вам розібратися в мірах відсутніх кутів.

    Керівництво

    Деякі спеціальні кутові пари ідентифікуються за їх сумою. Якщо вам відома міра одного кута, можна обчислити міру другого кута. Наприклад, додаткові кути завжди складаються до\(90^{\circ}\). Давайте розглянемо приклад.

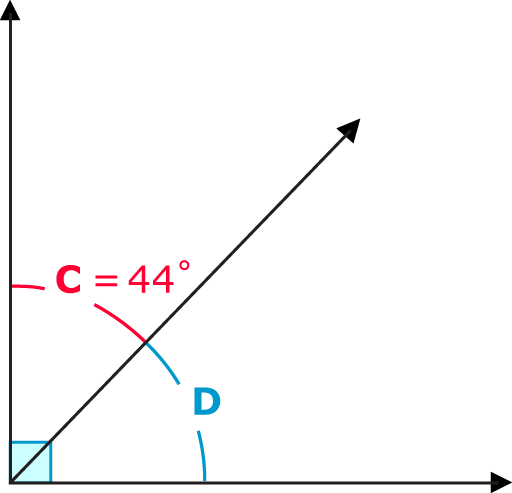    F-д_73С7Е900БФ 9ЕФ6557С63476Ф7Ф7ФС815FF42Д5Б0273EAB599FA7C02BCF+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{2}\)

    Разом\(C\) і\(D\) утворюють прямий кут. Тому вони взаємодоповнюють, і вони складаються до\(90^{\circ}\). \(C\)має міру\(44^{\circ}\).

    Щоб знайти вимір кута\(D\), просто відніміть міру кута\(C\) від\(90^{\circ}\).

    \(\angle C+\angle D=90^{\circ}\)

    \(44^{\circ}+\angle D=90^{\circ}\)

    \(\angle D=90−44\)

    \(\angle D=46^{\circ}\)

    \(D\)Тому кут вимірює\(46^{\circ}\). Перевірити розрахунок можна, додавши кути\(C\) і\(D\). Сума повинна дорівнювати\(90^{\circ}\).

    \(44^{\circ}+46^{\circ}=90^{\circ}\)

    Цей же процес може бути використаний для пошуку невідомого кута в парі додаткових кутів. Давайте розглянемо інший приклад.

    Кути\(P\) і\(Q\) є додатковими кутами. Якщо кут\(P\) вимірює\(112^{\circ}\), яка міра кута\(Q\)?

    Додаткові кути мають в цілому\(180^{\circ}\). Відніміть вимір\(P\), з\(180^{\circ}\) щоб знайти міру кута\(Q\).

    \(\angle P+\angle Q=180^{\circ}\)

    \(112^{\circ}+\angle Q=180^{\circ}\)

    \(\angle Q=180−112\)

    \(\angle Q=68^{\circ}\)

    Кут\(Q\) є\(68^{\circ}\). Перевірити розрахунок можна, додавши кути\(P\) і\(Q\). Пам'ятайте, щоб бути додатковими кутами, їх сума повинна дорівнювати\(180^{\circ}\).

    \(68^{\circ}+112^{\circ}=180^{\circ}\)

    Цей процес часто можна використовувати для пошуку міри невідомих кутів. Використовуйте логічні міркування для інтерпретації інформації, щоб знайти невідому міру.

    Погляньте на схему нижче.

    F-D_ЕД 725Ф КАД 4Е902 ЕДБ44282486 ЕАФ 87Ф93Б1 ЕБФ 4651661251E299C9+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{3}\)

    Керована практика

    Вирішити наступну проблему.

    Що таке міра кута\(R\)?

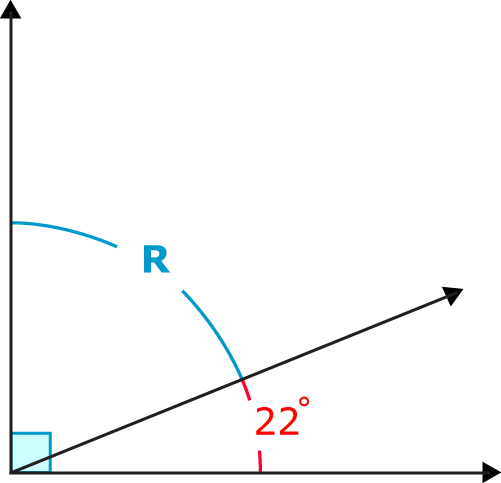    F-D_6A085BCCCA417FCF39E2F0БА53Д7Д98Б4611ЕС4067ББА667ББА 6606E82B00+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{4}\)

    Спочатку створимо рівняння, яке представляє зв'язок між двома кутами.

    \(R+22=90\)

    Далі віднімаємо заданий кут з суми двох кутів.

    \(R=90^{\circ}−22^{\circ}\)

    Потім розрахуйте різницю.

    Різниця є\(68^{\circ}\).

    Відповідь - кут\(R=68^{\circ}\).

    Міра невідомого кута є\(68^{\circ}\). Ви можете перевірити свою відповідь, поставивши це значення в for\(R\) у рівнянні.

    \(68+22=90^{\circ}\)

    Знайдіть доповнення або доповнення в кожному прикладі.

    Приклад\(\PageIndex{1}\)

    Кути\(A\) і\(B\) є взаємодоповнюючими. Кут\(A\) є\(33^{\circ}\). Знайдіть міру кута\(B\).

    Рішення

    Спочатку створимо рівняння, яке представляє співвідношення між кутами.

    \(33^{\circ}+B=90^{\circ}\)

    Далі віднімаємо заданий кут з суми двох кутів.

    \(B=90^{\circ}−33^{\circ}\)

    Потім розрахуйте різницю.

    Різниця є\(57^{\circ}\).

    Відповідь - кут\(B= 57^{\circ}\).

    Приклад\(\PageIndex{2}\)

    Кути\(C\) і\(D\) є додатковими. Кут С є\(59^{\circ}\). Знайдіть міру кута\(D\).

    Рішення

    Спочатку створимо рівняння, яке представляє співвідношення між кутами.

    \(59^{\circ}+D=180^{\circ}\)

    Далі віднімаємо заданий кут з суми двох кутів.

    \(D=180^{\circ}−59^{\circ}\)

    Потім розрахуйте різницю.

    Різниця є\(121^{\circ}\).

    Відповідь - кут\(D= 121^{\circ}\)

    Приклад\(\PageIndex{3}\)

    Кути\(A\) і\(B\) є додатковими. Кут\(A\) дорівнює 169^ {\ circ}. Знайдіть міру кута\(B\).

    Рішення

    Спочатку створимо рівняння, яке представляє співвідношення між кутами.

    \(169^{\circ}+B=180^{\circ}\)

    Далі віднімаємо заданий кут з суми кутів.

    \(B=180^{\circ}−169^{\circ}\)

    Потім розрахуйте різницю.

    Різниця є\(11^{\circ}\).

    Відповідь - кут\(B= 11^{\circ}\)

    Слідкуйте за

    F-D_9C82Б3БК22Б8Ф7ДБ0Ф05CB953753E329508БК6Ф17242363742E1250+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_jpgМалюнок\(\PageIndex{5}\)

    Пам'ятаєте Марко і його будинок? Якщо один шматок дерева має кутовий зріз\(55^{\circ}\), тобто, яка міра кутового зрізу для другого шматка дерева?

    Спочатку створимо рівняння, яке представляє зв'язок між двома кутами.

    \(55^{\circ}+M=90^{\circ}\)

    Далі віднімаємо заданий кут з суми двох кутів.

    \(M=90^{\circ}−55^{\circ}\)

    Потім розрахуйте різницю.

    Різниця є\(35^{\circ}\).

    Відповідь полягає в тому, що другий шматок дерева зрізається\(35^{\circ}\) під кутом.

    Відео-огляд

    Дізнатися більше

    Знайдіть міру відсутнього кута для кожної пари додаткових або додаткових кутів.

    1. Кути\(A\) і\(B\) є взаємодоповнюючими. Кут\(A\) є\(63^{\circ}\). Знайдіть міру кута\(B\).

    2. Кути\(A\) і\(B\) є взаємодоповнюючими. Кут\(A\) є\(83^{\circ}\). Знайдіть міру кута\(B\).

    3. Кути\(A\) і\(B\) є взаємодоповнюючими. Кут\(A\) є\(3^{\circ}\). Знайдіть міру кута\(B\).

    4. Кути\(A\) і\(B\) є взаємодоповнюючими. Кут\(A\) є\(23^{\circ}\). Знайдіть міру кута\(B\).

    5. Кути\(A\) і\(B\) є взаємодоповнюючими. Кут\(A\) є\(70^{\circ}\). Знайдіть міру кута\(B\).

    6. Кути\(A\) і\(B\) є взаємодоповнюючими. Кут\(A\) є\(29^{\circ}\). Знайдіть міру кута\(B\).

    7. Кути\(A\) і\(B\) є взаємодоповнюючими. Кут\(A\) є\(66^{\circ}\). Знайдіть міру кута\(B\).

    8. Кути\(A\) і\(B\) є взаємодоповнюючими. Кут\(A\) є\(87^{\circ}\). Знайдіть міру кута\(B\).

    9. Кути\(A\) і\(B\) є додатковими. Кут\(A\) є\(33^{\circ}\). Знайдіть міру кута\(B\).

    10. Кути\(A\) і\(B\) є додатковими. Кут\(A\) є\(103^{\circ}\). Знайдіть міру кута\(B\).

    11. Кути\(A\) і\(B\) є додатковими. Кут\(A\) є\(73^{\circ}\). Знайдіть міру кута\(B\).

    12. Кути\(A\) і\(B\) є додатковими. Кут\(A\) є\(78^{\circ}\). Знайдіть міру кута\(B\).

    13. Кути\(A\) і\(B\) є додатковими. Кут\(A\) є\(99^{\circ}\). Знайдіть міру кута\(B\).

    14. Кути\(A\) і\(B\) є додатковими. Кут\(A\) є\(110^{\circ}\). Знайдіть міру кута\(B\).

    15. Кути\(A\) і\(B\) є додатковими. Кут\(A\) є\(127^{\circ}\). Знайдіть міру кута\(B\).

    Лексика

    Термін Визначення
    Гострий кут Гострий кут - це кут з мірою менше 90 градусів.
    Додаткові кути Додатковими кутами є пара кутів з сумою 90.
    Тупий кут Тупий кут - це кут більше 90 градусів, але менше 180 градусів.
    Прямий кут Прямим кутом є пряма, рівна 180.
    Додаткові кути Додаткові кути - це два кути, сума яких становить 180 градусів.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Додаткові, Додаткові та Вертикальні кути

    Практика: Відсутні заходи взаємодоповнюючих та додаткових кутів

    Реальний світ: Пізанські вежі