Skip to main content
LibreTexts - Ukrayinska

1.12: Конструкції та бісектриси

  1. Last updated
  2. Save as PDF
  • Page ID
    54940

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Побудувати кути і відрізки лінії. Розділіть кути і відрізки лінії на дві конгруентні частини.

    Бісектриси відрізків та кутів

    Опишіть, як побудувати\(45^{\circ}\) кут за допомогою циркуля і прямолінійного краю.

    Бісектриси

    Конструкція схожа на креслення тим, що вона виробляє візуальний результат. Однак, хоча малюнки часто є просто приблизними ескізами, які допомагають передати ідею, конструкції - це покрокові процеси, що використовуються для створення точних геометричних фігур. Для створення конструкції своїми руками є кілька інструментів, які можна використовувати:

    1. Компас: Пристрій, що дозволяє створити коло із заданим радіусом. Компаси можуть не тільки допомогти вам створити кола, але також вони можуть допомогти вам копіювати відстані.
    2. Straightedge: Все, що дозволяє виробляти пряму лінію. Прямолінійний край не повинен вміти вимірювати відстані. Індексна картка добре працює як прямолінійний. Ви також можете використовувати лінійку як прямий край, якщо ви використовуєте її лише для малювання прямих ліній, а не для вимірювання.
    3. Папір: Коли геометрична фігура знаходиться на аркуші паперу, сам папір можна скласти, щоб побудувати нові лінії.

    Розділити відрізок або кут означає розділити його на дві конгруентні частини. Бісектриса відрізка лінії буде проходити через середину відрізка лінії. Перпендикулярна бісектриса відрізка проходить через середину відрізка лінії і перпендикулярна відрізку лінії. Для побудови бісектрис сегментів і кутів корисно запам'ятати деякі відповідні теореми:

    Будь-яка точка перпендикулярної бісектриси відрізка лінії буде рівновіддалена від кінцевих точок відрізка лінії. Це означає, що одним із способів знайти перпендикулярну бісектрису відрізка (наприклад,\(\overline{AB}\) нижче) є пошук двох точок, які є рівновіддаленими від кінцевих точок відрізка лінії (наприклад, C і D нижче) та з'єднати їх.

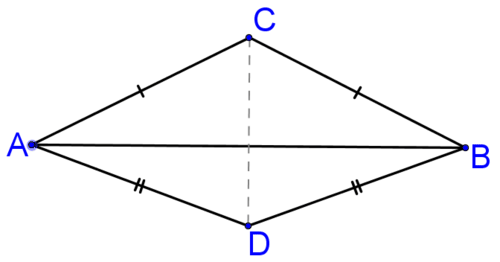    F-D_672E75926D28955EF63АБ2А279БК85ФА6А52С7А00093ФДБ75C7D8F5F+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_pngМалюнок\(\PageIndex{1}\)

    Будь-яка точка на бісектрисі кута буде рівновіддалена від променів, що створюють кут. Це означає, що одним із способів знайти бісектрису кута (наприклад,\(\angle BAC\) нижче) є пошук двох точок, рівновіддалених від променів, що створюють кут (наприклад, точки A та D нижче).

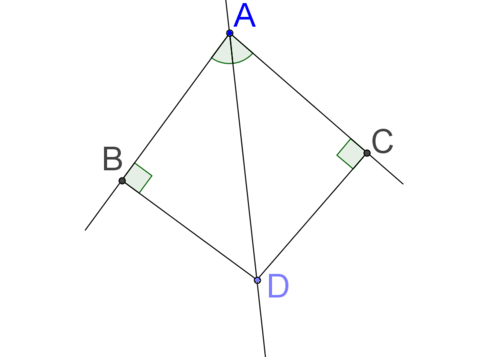    F-D_631F14D4AE545A3320425B7DC14B32CB9A67F1E6D7F2630CDFCB9+зображення_thumb_поштова листівка_крихітка+зображення_thumb_поштова листівка_крихітка_pngМалюнок\(\PageIndex{2}\)

    Давайте розглянемо різні способи пошуку перпендикулярної бісектриси відрізка лінії.

    1. Намалюйте відрізок лінії, як помаранчевий нижче, на аркуші паперу (прямокутник нижче представляє папір). Складіть папір для того, щоб знайти перпендикулярну бісектрису відрізка лінії.

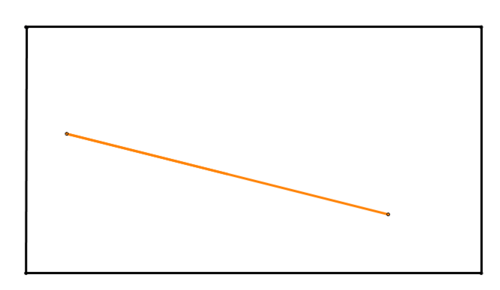    F-D_35792 FFCF137E0981D9EBEC B2EF0FCC700E9C0996380A3E123A38A1+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_pngМалюнок\(\PageIndex{3}\)

    Щоб знайти перпендикулярну бісектрису, складіть папір так, щоб кінцеві точки лежали один на одного. Роблячи це, ви точно зіставили дві половини відрізка лінії.

    Будь-яка точка на згині тепер рівновіддалена від обох кінцевих точок, тому що кінцеві точки тепер знаходяться в одному місці! Це означає, що складка, зроблена згином, буде перпендикулярною бісектрисою відрізка лінії.

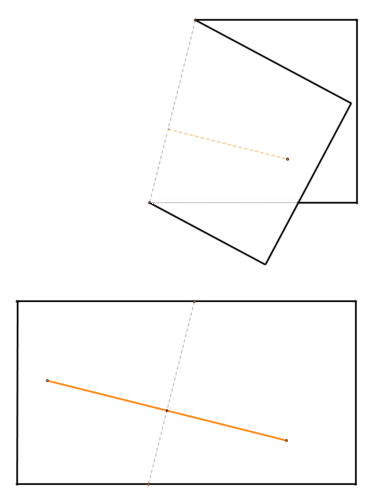    F-D_38E67158d88F233B1C990370 Ед 40А4А4Д 2685d51ad95635A607D4+зображення_thumb_поштова листівка_крихітка_зображення_великий палець_листівка_крихітка_pngМалюнок\(\PageIndex{4}\)

    2. Намалюйте відрізок лінії, як помаранчевий нижче, на аркуші паперу (прямокутник нижче представляє папір). Використовуйте циркуль і прямолінійний край, щоб знайти перпендикулярну бісектрису відрізка лінії.

    F-D_35792 FFCF137E0981D9EBEC B2EF0FCC700E9C0996380A3E123A38A1+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_pngМалюнок\(\PageIndex{5}\)

    Використовуйте компас, щоб намалювати коло по центру в кожній кінцевій точці з однаковим радіусом. Переконайтеся, що радіус кіл досить великий, щоб кола перетиналися. Якщо кола занадто великі, щоб поміститися на папері, намалюйте ту частину кола, яка поміщається на папері. Ось перше коло:

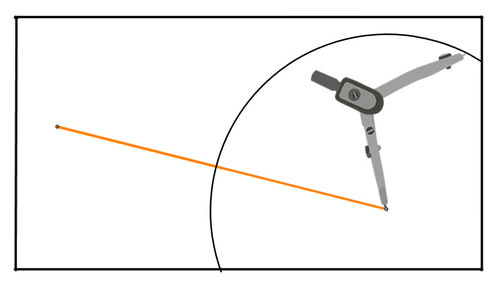    F-D_A71 ЕААД 0А35102Ф4КД94Б289276 ACF5935C1BEC8BDF901C9A58B916+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_jpgМалюнок\(\PageIndex{6}\)

    Ось друге коло:

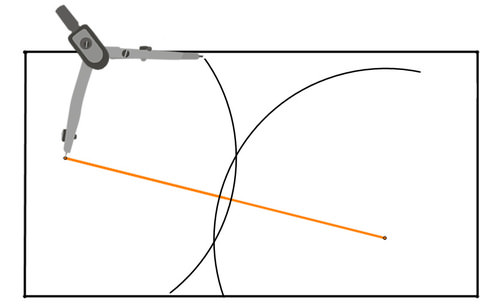    F-D_01EBCB63Ф79Б626675cd81E2d9b0d6a47cc7fd50ab9f63c5c62E4F+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_jpgМалюнок\(\PageIndex{7}\)

    Точки інтересу - це дві точки, де кола перетинаються. Оскільки радіус кожного кола однаковий, кожна з цих точок рівновіддалена від кінцевих точок відрізка лінії.

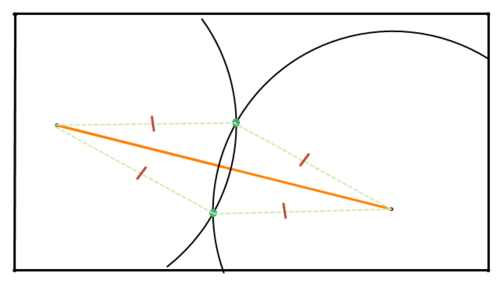    F-D_37C8188E4E4E4E0E8BE3E9BB9DD10E51A3472497FCF52A50051E99+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихіткий.PNGМалюнок\(\PageIndex{8}\)

    Тому кожна з цих точок лежить на перпендикулярній бісектрисі відрізка лінії. Використовуйте свій straightedge, щоб намалювати лінію, що з'єднує дві точки перетину. Це перпендикулярна бісектриса відрізка лінії.

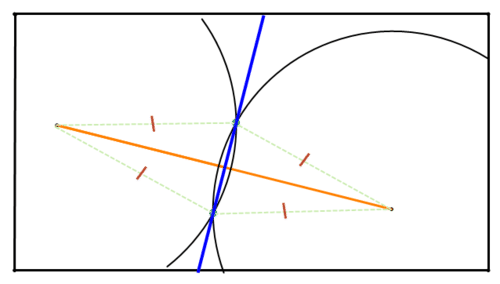    F-D_181C91A27535E8CEE7F6420F5F1B2216d965906028EA000A73F2+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_pngМалюнок\(\PageIndex{9}\)

    Як ви можете використовувати компас і straightedge, щоб знайти середину відрізка лінії?

    Одним із способів є використання процесу з прикладу B для побудови перпендикулярної бісектриси. Серединою відрізка лінії буде точкою, де перпендикулярна бісектриса перетинає відрізок лінії.

    Приклад\(\PageIndex{1}\)

    Раніше вас запитали, як побудувати\(45^{\circ}\) кут за допомогою циркуля і прямокутника.

    Один із способів побудови\(45^{\circ}\) кута полягає в тому, щоб:

    • Намалюйте відрізок і будуйте його перпендикулярну бісектрису. Це дасть вам\(90^{\circ}\) кути.
    • Побудувати бісектрису кута одного з цих\(90^{\circ}\) кутів. Це дозволить отримати два\(45^{\circ}\) кути. Примітка: Етапи побудови бісектриси кута досліджуються в питаннях керованої практики.

    Чи можете ви придумати інший спосіб побудувати ідеальний\(45^{\circ}\) кут за допомогою компаса і прямолінійного краю?

    Приклад\(\PageIndex{2}\)

    Намалюйте на аркуші паперу кут, подібний до наведеного нижче (прямокутник нижче представляє папір). Зверніть увагу, що два сегменти, що створюють кут, НЕ повинні бути однакової довжини. Складіть папір, щоб створити бісектрису кута.

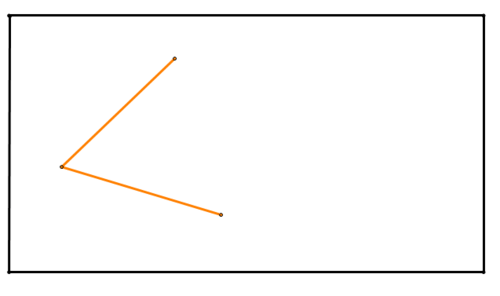    F-D_F8D17F9a9C462BD46AC35C1575CC601099CBFC2C396B02C601d08b7E+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_pngМалюнок\(\PageIndex{10}\)

    Рішення

    Складіть папір так, щоб один відрізок перекривав інший відрізок. Сгином буде бісектриса кута.

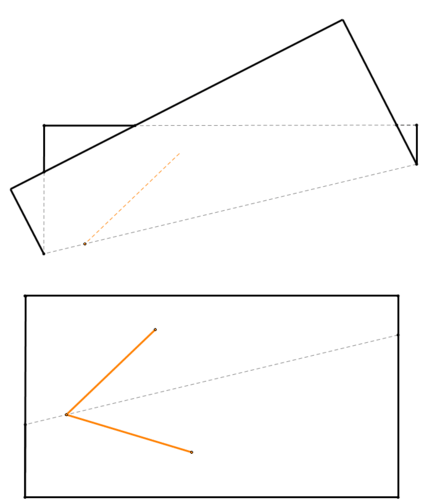    F-D_D4CDFF2173376C321DC35a2F06310b5AB8E66005BD65DF598AE1C0E4+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_pngМалюнок\(\PageIndex{11}\)

    Приклад\(\PageIndex{3}\)

    Намалюйте на аркуші паперу кут, подібний до наведеного нижче (прямокутник нижче представляє папір). Зверніть увагу, що два сегменти, що створюють кут, НЕ повинні бути однакової довжини. Використовуйте компас і прямолінійний край, щоб знайти бісектрису кута.

    F-D_F8D17F9a9C462BD46AC35C1575CC601099CBFC2C396B02C601d08b7E+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_pngМалюнок\(\PageIndex{12}\)

    Рішення

    Використовуйте компас, щоб створити частину кола з центром у вершині кута, яка проходить через обидва сегменти, створюючи кут:

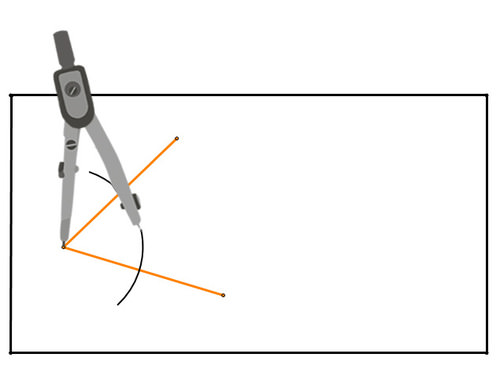    F-D_090130027146C81A5C80AE7DF3CDB421DC726F4E924A4B5E53D3B63+зображення_thumb_поштова листівка_крихіткий+зображення_thumb_поштова листівка_крихітка_jpgМалюнок\(\PageIndex{13}\)
    Створіть два кола з однаковим радіусом по центру в кожній точці перетину дуги та двох сегментів. Переконайтеся, що радіус досить великий, щоб кола перекривалися. Ось перше коло:
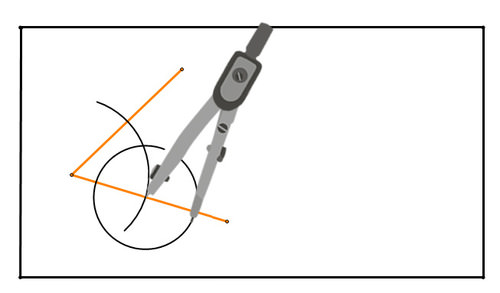    F-D_AFE1AC1C2533A31B61 EAB8F94E43480A0D Fea6A30F9C3687DBA6CE+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_jpgМалюнок\(\PageIndex{14}\)

    Ось друге коло:

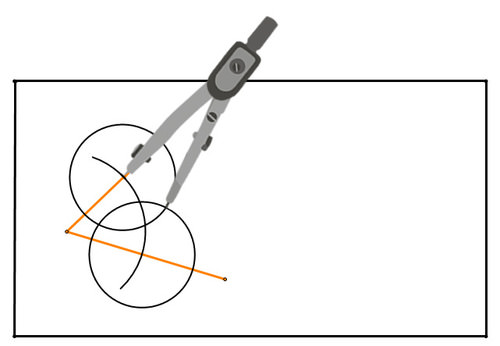    F-D_13FCF8E44D903BF03A12257ed8d6ce8A1F287A5215897E5F387B+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_jpgМалюнок\(\PageIndex{15}\)

    Точки, де кола перетинаються, рівновіддалені від сегментів, що створюють кут. Тому вони визначають бісектрису кута. З'єднайте ці точки перетину, щоб створити бісектрису кута:

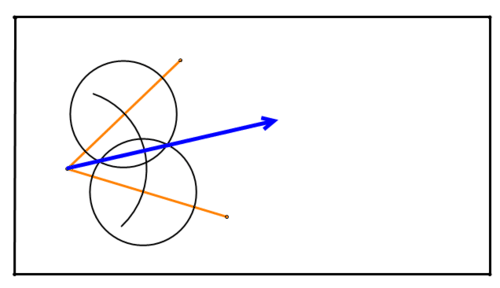    F-D_14d4b9BA2A4181A819B4F06F40410C4D2876d824d58c2716a99cd2+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_pngМалюнок\(\PageIndex{16}\)

    Приклад\(\PageIndex{4}\)

    Доведіть, що кут бісектриса, створений за допомогою методу в #2 насправді кут бісектриса.

    Розглянемо конструкцію з #2 нижче. Точки були позначені, і два додаткових сегмента були намальовані (показано зеленим кольором):

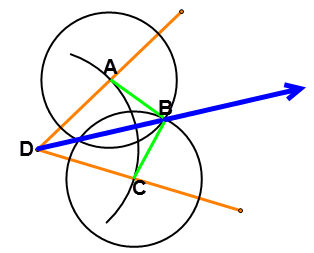    F-D_016d4857FB2F9253679D64246A873985BD0C3BD1E73EF168E1049+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png\(\Індекс сторінки малюнка {17}\)

    Рішення

    На цій картині\(\oveline{AD} \cong \overline{CD}\)because they are both radiuses of the same partial circle centered at point \(D\). \(\overline{AB} \cong \oveline{CB}\) because they are both radiuses of congruent circles centered at \(A\) and \(C\) respectively. \(\overline{BD} \cong \overline{BD}\) by the reflexive property. Therefore, \(\Delta ABD \cong \Delta CBD\) by \(SSS \cong\). \(\angle ADB \cong \angle BDC\) because they are corresponding parts of congruent triangles. Therefore, \(\overrightarrow{BD}\) must be the angle bisector of \(\angle ADC\).

    Review

    1. What does it mean to bisect a segment or an angle?
    2. Describe the steps for finding the perpendicular bisector of a line segment.
    3. Describe how to use the perpendicular bisector of a line segment to find the midpoint of the line segment.
    4. What's the difference between a bisector and a perpendicular bisector? How can you construct a non-perpendicular bisector of a line segment?
    5. Draw a line segment on your paper and construct the perpendicular bisector of the segment.
    6. Draw another line segment on your paper and construct the perpendicular bisector of that segment using another method.
    7. Draw an angle on your paper and construct the bisector of the angle.
    8. Draw another angle on your paper and construct the bisector of that angle using another method.
    9. Use your straightedge to draw a triangle on your paper. Construct the angle bisector of each angle. What point have you found?
    10. Use your straightedge to draw a triangle on your paper. Construct the perpendicular bisector of each side of the triangle. What point have you found?
    11. Use the triangle and your work from #10. Construct the medians of the triangle. What point have you found?
    12. Compare and contrast the two methods for finding a bisector-paper folding vs. compass and straightedge.
    13. Construct a \(45^{\circ}\) angle (look at the concept problem for help). Then, construct a \(22.5^{\circ}\) angle.
    14. Construct an isosceles right triangle. Hint: Start by creating a right angle by constructing a perpendicular bisector.
    15. If possible, extend your construction of an isosceles right triangle to construct a square. Describe your steps.

    Review (Answers)

    To see the Review answers, open this PDF file and look for section 5.2.

    Vocabulary

    Term Definition
    perpendicular bisector A perpendicular bisector of a line segment passes through the midpoint of the line segment and intersects the line segment at \(90^{\circ}\).
    Ray A ray is a part of a line that has one endpoint and continues indefinitely in one direction.
    Bisector A bisector divides a line segment or angle into two congruent parts.

    Additional Resource

    Interactive Element