1.8: Ідентифікація кутів по вершині та промені
- Page ID
- 54927
Дізнайтеся, як називати кути за допомогою букв.
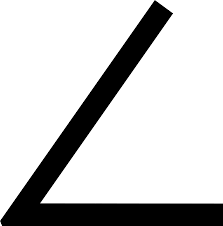 Малюнок\(\PageIndex{1}\)
Малюнок\(\PageIndex{1}\)Доньолл ходить від свого будинку до своєї школи. Потім, після школи, він ходить до будинку свого друга. Він зауважує, що його подорож утворює кут. Він вирішує назвати кут. Donyell позначає свій будинок як точку\(H\), свою школу як точку S і будинок свого друга як точку\(F\). Чи можете ви використовувати точки для назви кута, утвореного його подорожжю?
У цій концепції ви дізнаєтеся про частини кута.
Визначення кутів по вершині та промені
Кут - одна з ключових геометричних фігур, з якими ви будете працювати в геометрії. Кут створюється, коли два промені з'єднуються в загальній точці.
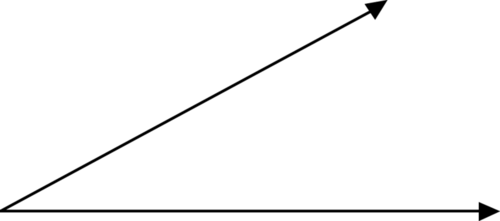 Малюнок\(\PageIndex{2}\)
Малюнок\(\PageIndex{2}\)Ви можете бачити, що два промені з'єднані в загальній кінцевій точці, яка називається вершиною. Це формує кут. Кут називається точками на променях.
Давайте розглянемо на прикладі кута.
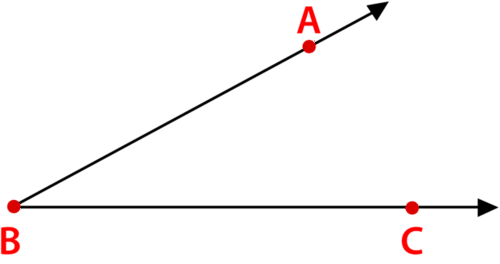 Малюнок\(\PageIndex{3}\)
Малюнок\(\PageIndex{3}\)Це кут\(ABC\). Вершина завжди\(B\) знаходиться посередині. Символ для кута виглядає як невеликий кут.
\(\angle ABC\)
\(ABC\)Кут названий цим символом.
Приклад\(\PageIndex{1}\)
Раніше вам дали проблему про Доньєлл і його прогулянку до школи, а потім до будинку його друга.
Назвіть кут, якщо його будинок - точка\(H\), його школа - точка,\(S\) а будинок його друга - точка\(F\).
Рішення
Для початку визначте загальну кінцеву точку.
\(S\)
Потім назвіть кут.
\(\angle HSF\)
Відповідь є\(\angle HSF\).
Приклад\(\PageIndex{2}\)
Яка загальна кінцева точка променів, що утворюються\(\angle HIJ\)?
Рішення
Спочатку визначте назву загальної кінцевої точки.
Вершина
Далі слід визначити місце розташування вершини в назві кута.
Середня точка
Потім напишіть крапку.
\(I\)
Відповідь є\(I\). Загальною кінцевою точкою променів, які утворюються,\(\angle HIJ\) є\(I\).
Приклад\(\PageIndex{3}\)
Назвіть цей кут. Переконайтеся, що вершина знаходиться посередині.
 Малюнок\(\PageIndex{4}\)
Малюнок\(\PageIndex{4}\)Рішення
Спочатку знайдіть загальну кінцеву точку.
\(E\)
Потім назвіть кут.
\(\angle DEF\)
Відповідь є \(\angle DEF\).
Приклад\(\PageIndex{4}\)
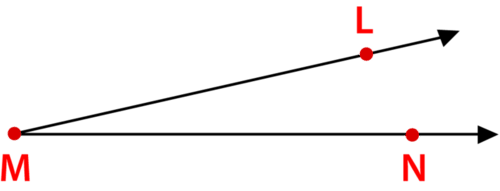 Малюнок\(\PageIndex{5}\)
Малюнок\(\PageIndex{5}\)Рішення
Спочатку знайдіть загальну кінцеву точку.
\(M\)
Потім назвіть кут.
\(\angle LMN\)
Відповідь:\(\angle LMN\)
Приклад\(\PageIndex{5}\)
Яка загальна кінцева точка променів, що утворюються\(\angle QRS\)?
Рішення
Спочатку визначте назву загальної кінцевої точки.
Вершина
Далі слід визначити місце розташування вершини в назві кута.
Середня точка
Потім напишіть крапку.
\(R\)
Відповідь є\(R\). Загальною кінцевою точкою променів, які утворюються,\(\angle QRS\) є\(R\).
Рецензія
Намалюйте малюнок, щоб проілюструвати кожну з названих геометричних фігур.
- \(\overrightarrow{AB}\)
- \(\overleftrightarrow{CD}\)
- \(\overleftrightarrow{DE}\)
- \(\angle ABC\)
- \(\angle LMN\)
- \(\overline{XY}\)
- \(\overrightarrow{PQ}\)
- \(\overleftrightarrow{GH}\)
- \(\overleftrightarrow{AB} \parallel \overleftrightarrow{DE}\)
- \(\overleftrightarrow{LM} \parallel \overleftrightarrow{DE}\)
- \(\overleftrightarrow{RS} \parallel \overleftrightarrow{TU}\)
- \(\overline{DF} \parallel \overline{XY}\)
Визначте наступні терміни.
- Рей
- Лінія
- Вершина
- Відрізок лінії
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 9.3.
Лексика
| Термін | Визначення |
|---|---|
| Кут | Геометрична фігура, утворена двома променями, які з'єднуються в одній точці або вершині. |
| Лінії, що перетинаються | Пересічні лінії - це лінії, які перетинаються або зустрічаються в якійсь точці. |
| лінія | Лінія - це пряма одновимірна фігура, яка вічно тягнеться в протилежні сторони. |
| відрізок лінії | Відрізок лінії — це частина лінії, яка має дві кінцеві точки. |
| Паралельний | Дві або більше ліній паралельні, коли вони лежать в одній площині і ніколи не перетинаються. Ці лінії завжди будуть мати однаковий ухил. |
| Точка | Точка - це місце в просторі, яке не має розміру або форми. |
| Точка перетину | Точка перетину - це точка, де зустрічаються дві пересічні лінії. |
| Рей | Промінь - це частина лінії, яка має одну кінцеву точку і триває нескінченно довго в одному напрямку. |
| Вершина | Вершина - це точка перетину ліній або променів, які утворюють кут. |
Додатковий ресурс
Інтерактивний елемент
Відео: Введення в кути
Практика: Ідентифікація кутів по вершині та промені