1.15: Додаткові кути

Last updated

Oct 27, 2022
Save as PDF
- 1.14: Додаткові кути
- 1.16: Відсутні заходи взаємодоповнюючих та додаткових кутів

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Два кута, які додають до 180 градусів і при сусідніх утворюють пряму лінію.

Лінійні пари

Два кути суміжні, якщо вони мають однакову вершину, мають спільну сторону і не перекриваються. $\angle PSQ$ і $\angle QSR$ є суміжними.

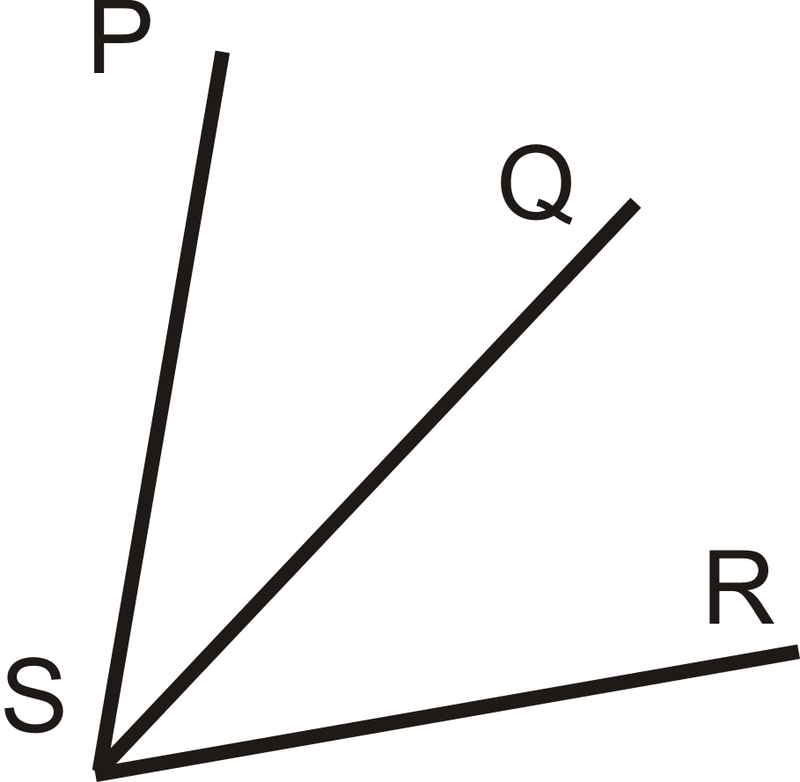F-д_948Ф9829 ЕБА 73297972А091Б94ДД4 ЕБ5А471Д8Е63 ББ9756AF1D4E81F+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{1}$

Лінійна пара - це два кути, які є суміжними і чиї непоширені сторони утворюють пряму лінію. Якщо два кути є лінійною парою, то вони є додатковими (складають до $180^{\circ}$ ). $\angle PSQ$ і $\angle QSR$ являють собою лінійну пару.

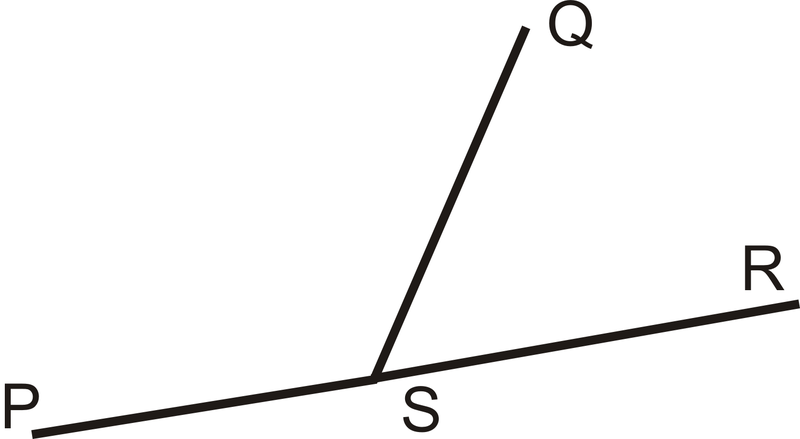F-д_23д540Е9Б 461С6Е22261 АА41532С5Д3Б85Ф23Ф2СА346Д29А61С4357+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{2}$

Що робити, якщо вам дали два кути невідомого розміру і сказали, що вони утворюють лінійну пару? Як би ви визначили їх кутові заходи?

Наприклад $\PageIndex{1}$ і $\PageIndex{2}$ , скористайтеся схемою нижче. Зауважте, що $\overline{NK} \perp \overleftrightarrow{IL}$ .

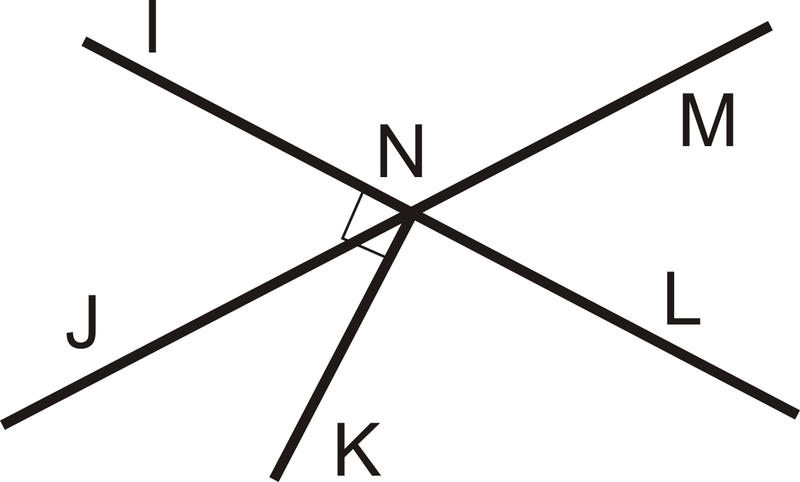F-дддбф де 705ABDE 0CDC132cdcd 782 БК 102Ф8Б34С4Б23А3АБ4Ф4862ЦА+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{3}$

Приклад $\PageIndex{1}$

Назвіть одну лінійну пару кутів.

Рішення

$\angle MNL$ і $\angle LNJ$

Приклад $\PageIndex{2}$

Що таке $m \angle INL$ ?

Рішення

$180^{\circ}$

Приклад $\PageIndex{3}$

Яка міра кожного кута?

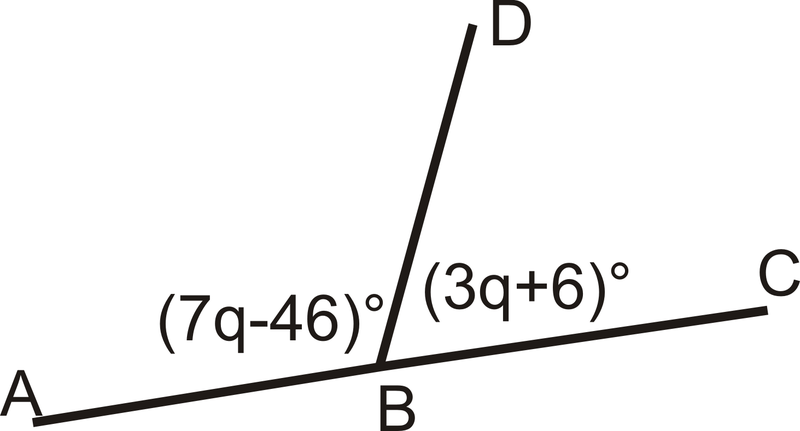Ф-д_8 БЦК 55351ДА12БФ7020Е7186БК 467135Е5ДБ11Б290А133521Д+зображення_крихіткий+зображення_крихіткий_крихіткий.PNG — Малюнок $\PageIndex{4}$

Рішення

Ці два кути є лінійною парою, тому вони складаються до $180^{\circ}$ .

$(7q−46)^{\circ}+(3q+6)^{\circ}=180^{\circ}$

$10q−40^{\circ}=220^{\circ}$

$10q=180^{\circ}$

$q=22^{\circ}$

Підключіть q, щоб отримати міру кожного кута.

$m \angle ABD=7(22^{\circ})−46^{\circ}=108^{\circ}$

$m \angle DBC=180^{\circ}−108^{\circ}=72^{\circ}$

Приклад $\PageIndex{4}$

Є $\angle CDA$ і $\angle DAB$ лінійна пара? Чи є вони додатковими?

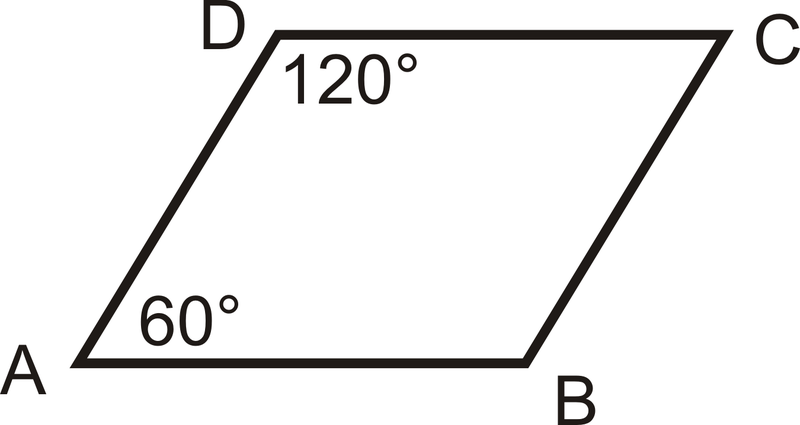F-д_3С72А 69Д58607С8БКД 2ЕС43АФ9Ф9Ф9Д1233Ф828398С238Е97644КС7Е0D+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{5}$

Рішення

Два кути не є лінійною парою, оскільки вони не мають однакової вершини. Вони є додатковими, оскільки складаються $180^{\circ}: 120^{\circ}+60^{\circ}=180^{\circ}$ .

Приклад $\PageIndex{5}$

Знайдіть міру кута, який утворює лінійну пару з $\angle MRS$ if $m \angle MRS$ is $150^{\circ}$ .

Рішення

Оскільки лінійні пари повинні складатися $180^{\circ}$ , інший кут повинен бути $180^{\circ}−150^{\circ}=30^{\circ}$ .

Рецензія

Для 1-5 визначте, чи є твердження істинним чи хибним.

Лінійні пари конгруентні.
Сусідні кути мають спільну вершину.
Сусідні кути перекриваються.
Лінійні пари є додатковими.
Додаткові кути утворюють лінійні пари.

Для вправи 6 знайдіть значення $x$ .

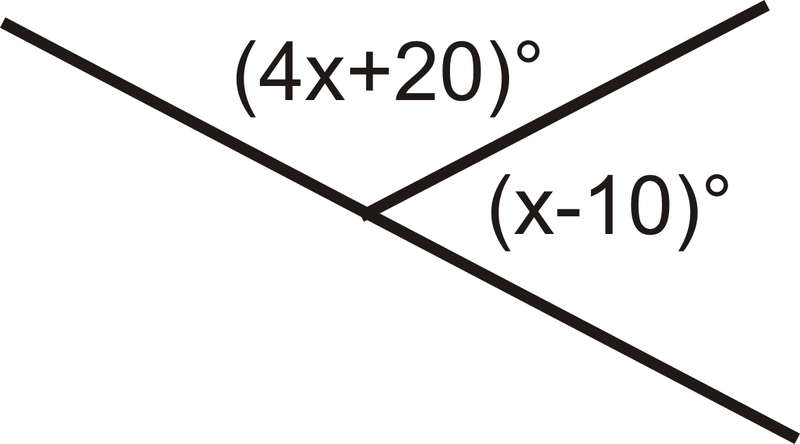Малюнок $\PageIndex{6}$

Знайдіть міру кута, який утворює лінійну пару з $\angle MRS$ $m \angle MRS$ if:

$61^{\circ}$
$23^{\circ}$
$114^{\circ}$
$7^{\circ}$
$179^{\circ}$
$z^{\circ}$

Огляд (Відповіді)

Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 1.9.

Лексика

Термін	Визначення
Сусідні кути	Два кута є суміжними, якщо вони поділяють сторону і вершину. Слово «суміжний» означає «поруч» або «поруч з».
лінійна пара	Два кути утворюють лінійну пару, якщо вони є додатковими і сусідніми.
Діаграма	Діаграма - це малюнок, який використовується для представлення математичної задачі.

Додаткові ресурси

Інтерактивний елемент

Відео: Додаткові, Додаткові та Вертикальні кути

Діяльність: Додаткові кути обговорення Питання

Навчальні посібники: Керівництво з вивчення кутів

Практика: Додаткові кути

Реальний світ: додаткові кути