Skip to main content
LibreTexts - Ukrayinska

1.17: Вертикальні кути

  1. Last updated
  2. Save as PDF
  • Page ID
    54982

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Зрозумійте, що вертикальні кути знаходяться один навпроти одного і мають однакову міру.

    Вертикальні кути - це два несуміжних кута, утворених пересічними лініями. \(\angle 1\)і\(\angle 3\) є вертикальними кутами і\(\angle 2\) і\(\angle 4\) є вертикальними кутами.

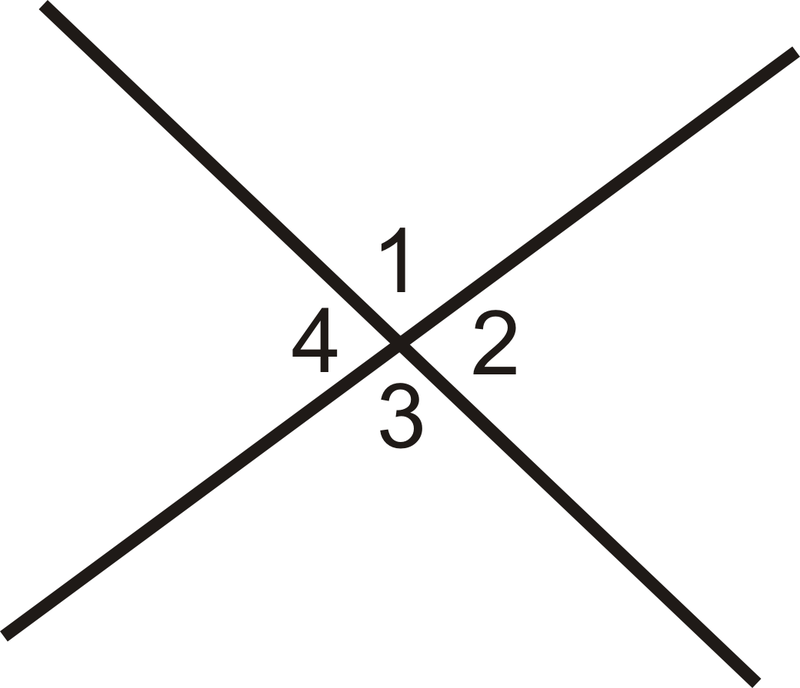    F-д_Б 1875593889АА9Ф44Б649А8Д51Е5074 Ф39АФ4579Ф8553Е621Д7ЕФЦ5+зображення_крихіткий+зображення_крихіткий_PNGМалюнок\(\PageIndex{1}\)

    Теорема вертикальних кутів стверджує, що якщо два кути є вертикальними кутами, то вони є конгруентними.

    Що робити, якщо вам дали два кути невідомого розміру і сказали, що вони вертикальні кути? Як би ви визначили їх кутові заходи?

    Приклад\(\PageIndex{1}\)

    Знайдіть значення\(x\).

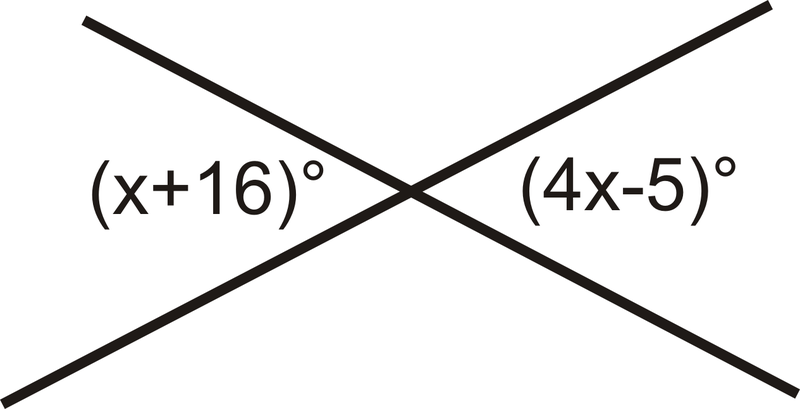    Ф-Д_Б1114С5А2БФ 758Ф3С020СА1ДФ 1ДФ 2034Д4Ф 359C434E1847025242+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{2}\)

    Рішення

    Вертикальні кути конгруентні, тому встановіть кути рівні один одному і вирішуйте для\(x\).

    \(x+16=4x−5\)

    \(3x=21\)

    \(x=7^{\circ}\)

    Приклад\(\PageIndex{2}\)

    Знайдіть значення\(y\).

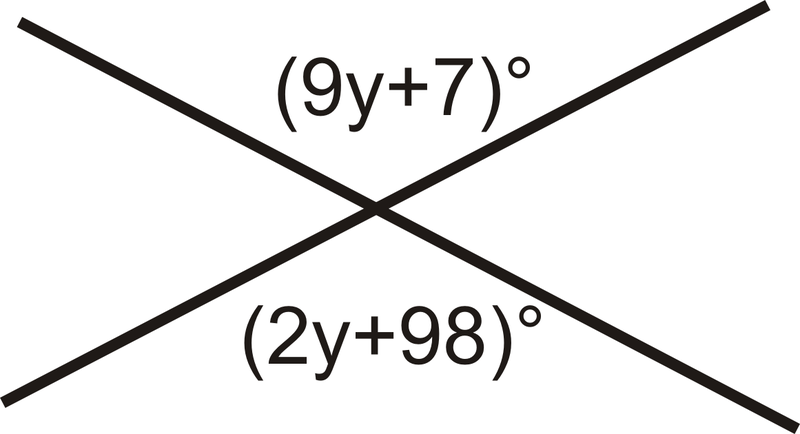    Ф-Д_С192СС4Ф78143E455258C341d97E20686E7CFF12A5EC2C5465506CF7+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{3}\)

    Рішення

    Вертикальні кути конгруентні, тому встановіть кути рівні один одному і вирішуйте для\(y\).

    \(9y+7=2y+98\)

    \(7y=91\)

    \(y=13^{\circ}\)

    Приклад\(\PageIndex{3}\)

    Знайти\(m\angle 1\).

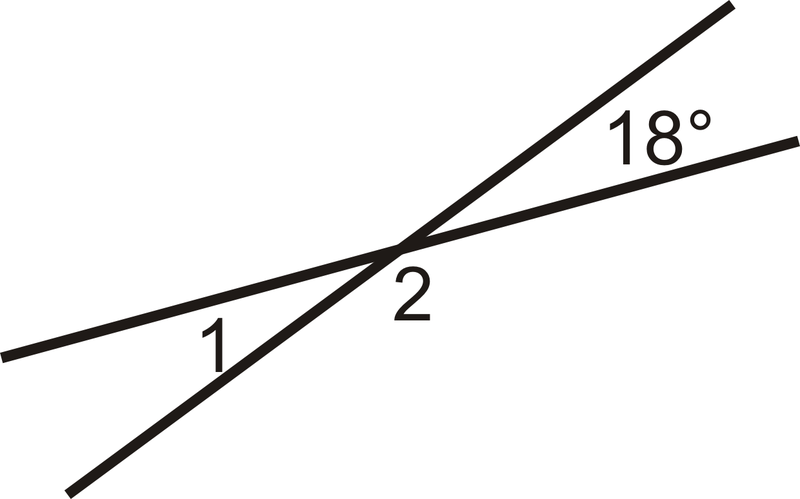    F-D_450Ф99639 ААА9618ЕД 92Б9Д2С1Д0Ф7Д5Ф39640А56 ACDF0957A3D+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{4}\)

    Рішення

    \(\angle 1\)це вертикальні кути з\(18^{\circ}\), так\ (m\ кут 1=18^ {\ circ}.

    Приклад\(\PageIndex{4}\)

    Якщо\ кут ABC і\ кут DEF є вертикальними кутами і\ (m\ кут ABC = (4x+10) ^ {\ circ} і\ (m\ кут DEF = (5x+2) ^ {\ circ}, яка міра кожного кута?

    Рішення

    Вертикальні кути є конгруентними, тому встановіть кути рівні один одному і вирішуйте для х, а потім поверніться назад, щоб знайти міру кожного кута.

    \(4x+10=5x+2\)

    \(x=8\)

    Отже,\(m\angle ABC=m\angle DEF=(4(8)+10)^{\circ}=42^{\circ}\)

    Приклад\(\PageIndex{5}\)

    True або false: вертикальні кути завжди менше 90^ {\ circ}.

    Рішення

    Це помилково, ви можете мати вертикальні кути, які перевищують 90^ {\ circ}. Вертикальні кути менше 180^ {\ circ}.

    Рецензія

    Використовуйте схему нижче для вправ 1-2. Зауважте, що\(\overline{NK} \perp \overleftrightarrow{IL}\).

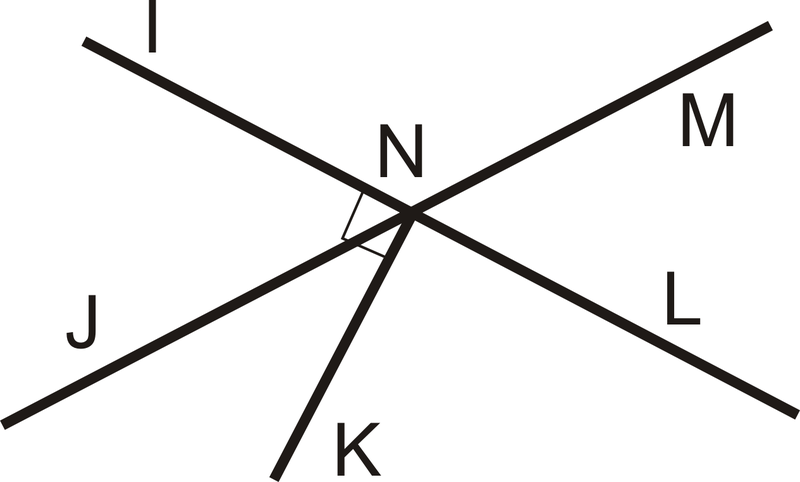    F-дддбф де 705ABDE0CDC132cdcd 782 БК 102Ф8Б34С4Б23А3АБ4Ф4862ЦА+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{5}\)
    1. Назвіть одну пару вертикальних кутів.
    1. Якщо\(m\angle INJ=63^{\circ}\), знайдіть\(m\angle MNL\).

    Для вправи 3 визначте, чи є твердження істинним чи хибним.

    1. Вертикальні кути мають однакову вершину.
    1. Якщо\(\angle ABC\) і\(\angle DEF\) є вертикальними кутами\(m\angle ABC=(9x+1)^{\circ}\) і і\(m\angle DEF=(5x+29)^{\circ}\), яка міра кожного кута?
    2. Якщо\(\angle ABC\) і\(\angle DEF\) є вертикальними кутами\(m\angle ABC=(8x+2)^{\circ}\) і і\(m\angle DEF=(2x+32)^{\circ}\), яка міра кожного кута?
    3. Якщо\(\angle ABC\) і\(\angle DEF\) є вертикальними кутами\(m\angle ABC=(x+22)^{\circ}\) і і\(m\angle DEF=(5x+2)^{\circ}\), яка міра кожного кута?
    4. Якщо\(\angle ABC\) і\(\angle DEF\) є вертикальними кутами\(m\angle ABC=(3x+12)^{\circ}\) і і\(m\angle DEF=(7x)^{\circ}\), яка міра кожного кута?
    5. Якщо\(\angle ABC\) і\(\angle DEF\) є вертикальними кутами\(m\angle ABC=(5x+2)^{\circ}\) і і\(m\angle DEF=(x+26)^{\circ}\), яка міра кожного кута?
    6. Якщо\(\angle ABC\) і\(\angle DEF\) є вертикальними кутами\(m\angle ABC=(3x+1)^{\circ}\) і і\(m\angle DEF=(2x+2)^{\circ}\), яка міра кожного кута?
    7. Якщо\(\angle ABC\) і\(\angle DEF\) є вертикальними кутами\(m\angle ABC=(6x−3)^{\circ}\) і і\(m\angle DEF=(5x+1)^{\circ}\), яка міра кожного кута?

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 1.10.

    Ресурси

    Лексика

    Термін Визначення
    Вертикальні кути Вертикальні кути - це пара протилежних кутів, створених пересічними лініями.
    Теорема про вертикальні кути Теорема вертикальних кутів стверджує, що якщо два кути вертикальні, то вони є конгруентними.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Додаткові, Додаткові та Вертикальні кути

    Діяльність: Вертикальні кути обговорення Питання

    Навчальні посібники: Керівництво з вивчення кутів

    Практика: Вертикальні кути

    Реальний світ: Вертикальні кути