Skip to main content
LibreTexts - Ukrayinska

1.13: Кутові властивості та теореми

  1. Last updated
  2. Save as PDF
  • Page ID
    54984

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Знайдіть кути та відрізки ліній та визначте, чи конгруентні фігури, а лінії паралельні. Зрозумійте додаткові кути як кути, сума яких становить 90 градусів, а додаткові кути як кути, сума яких становить 180 градусів.

    Міри кутових пар

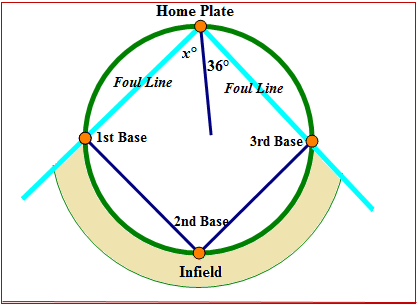
    F-D_801A9ДК1А555E719E56792471842041 DCE0B3A9B2B4B2CE141B56C3+зображення_thumb_поштова листівка_крихітка+зображення_thumb_поштова листівка_крихітка_jpgМалюнок\(\PageIndex{1}\)

    Фол лінії бейсбольного алмазу перетинаються в будинку пластини, утворюючи прямий кут. Бейсбол потрапляє з домашньої плити і утворює кут\(36^{\circ}\) з третьою базою фол лінії. Яка міра кута між першою базовою лінією фолу і ванною бейсболу?

    F-D_5E364161FF7BDCCD270AFCE50F99263FF6D8C2457AECB8BDBD BD2D30+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_pngМалюнок\(\PageIndex{2}\)

    Як ви можете використовувати свої знання кутів, щоб з'ясувати міру кута?

    У цій концепції ви дізнаєтеся міру кутових пар.

    Вимірювання кутових пар

    Існують різні типи кутових пар. Вертикальні кути - це кутова пара, утворена пересічними лініями таким чином, щоб вони ніколи не були сусідніми. Вони мають загальну вершину і ніколи не мають спільної сторони. Вертикальні кути рівні за мірою. На наступній схемі показані вертикальні кутові пари.

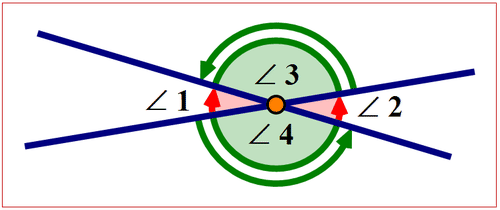    F-D_4B4F1A1482E421E1474ce5da0c53fd6FF3CFD55b587a0AB3B7844612+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_pngМалюнок\(\PageIndex{3}\)

    \(\angle 1\)і\(\angle 2\) є вертикальними кутами. \(m\angle 1=m\angle 2\)

    \(\angle 3\)і\(\angle 4\) є вертикальними кутами. \(m\angle 3=m\angle 4\)

    Сусідні кути - це кутова пара, також утворена двома пересічними лініями. Сусідні кути знаходяться поруч, мають загальну вершину і мають спільну сторону. На наступній схемі показані пари сусідніх кутів.

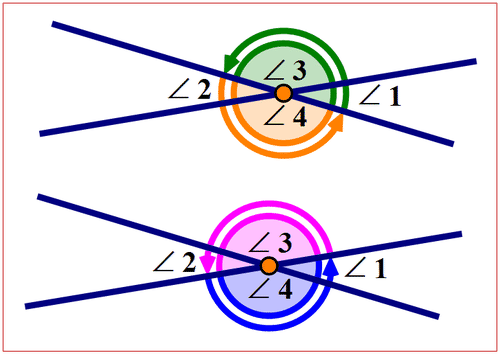    F-D_DA7EBA9AB20D9E87930E8DDB10817C9AE2BF43433D3D3D66D7D62+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_pngМалюнок\(\PageIndex{4}\)

    Кожна пара сусідніх кутів утворює прямий кут. Тому сума будь-яких двох сусідніх кутів дорівнює\(180^{\circ}\).

    \(m\angle 1+m \angle 3= 180^{\circ}\)

    \(m\angle 2+m \angle 4= 180^{\circ}\)

    \(m\angle 2+m \angle 3= 180^{\circ}\)

    \(m\angle 1+m \angle 4= 180^{\circ}\)

    Якщо сума двох кутів дорівнює,\(180^{\circ}\) то кути називаються додатковими кутами. На наступній схемі показані два додаткових кута.

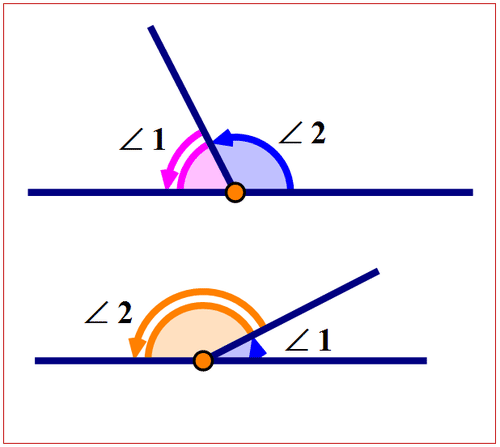    F-D_25C949Ф43ДК 69D277B20A72C7A4D27B3E9C71C2F43EAB8FD9CE4B09+зображення_thumb_поштова листівка_крихітка+зображення_thumb_поштова листівка_крихітка_pngМалюнок\(\PageIndex{5}\)

    В обох діаграмах,\(m\angle 1+m \angle 2= 180^{\circ}\).

    Якщо сума двох кутів дорівнює 90°, то кути називаються взаємодоповнюючими кутами. На наступній схемі показані два взаємодоповнюючих кута.

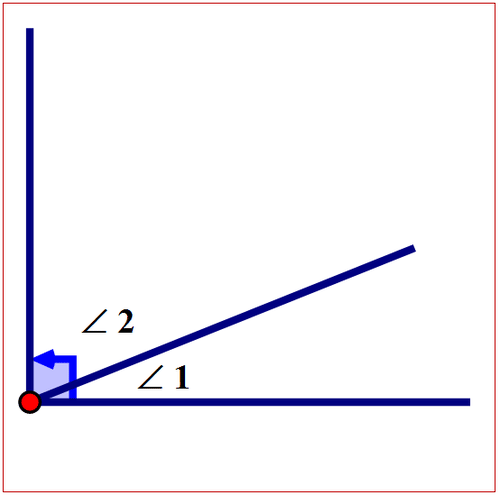    F-D_8cd88407D30E0A57 ADFF38E18591D699AFA ADF174DF58CF69807B336+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_pngМалюнок\(\PageIndex{6}\)

    \(m\angle 1+m \angle 2= 90^{\circ}\)

    Давайте застосуємо всю цю інформацію про кути і їх міру для визначення міри\(\angle a\)\(\angle b\), на\(\angle c\) наступній схемі.

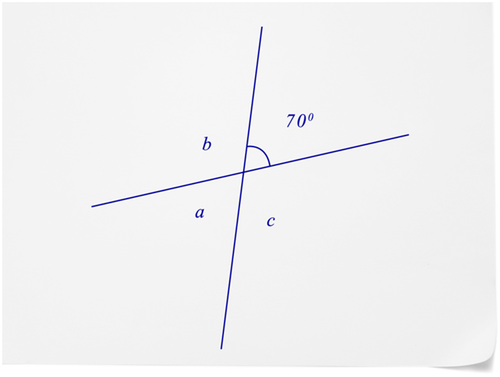    F-D_F7A0063A06C3EB0150ce3d78a05FAB9E50FBB286E3c19FC7ec563F+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_pngМалюнок\(\PageIndex{7}\)

    Існує чотири кути, утворені пересічними лініями. Міра одного з кутів є\(70^{\circ}\).

    Спочатку сформулюйте взаємозв'язок між кутом\(70^{\circ}\) і\(\angle b\).

    Кут\(70^{\circ}\). примикає до\(\angle b\) і два кути утворюють прямий кут.

    Далі виражаємо відносини за допомогою символів.

    \(\angle b+70^{\circ}=180^{\circ}\)

    Далі відніміть 70° з обох сторін рівняння.

    \(\angle b+70^{\circ}=180^{\circ}\)

    \(\angle b+70^{\circ}- 70^{\circ}=180^{\circ}-70^{\circ}\)

    Потім спростіть обидві сторони рівняння.

    \(\angle b+70^{\circ}- 70^{\circ}=180^{\circ}-70^{\circ}\)

    \(\angle b = 110^{\circ}\)

    Відповідь є\(110^{\circ}\).

    \(m \angle b = 110^{\circ}\)

    Спочатку сформулюйте взаємозв'язок між кутом\(70^{\circ}\) і\(\angle a\).

    Кут\(70^{\circ}\) і\(\angle a\) є вертикальними кутами і рівні за мірою.

    Далі виражаємо відносини за допомогою символів.

    \(m\angle a=70^{\circ}\)

    Відповідь є\(70^{\circ}\).

    \(m\angle a=70^{\circ}\)

    Спочатку викласти залежність між кутом\(70^{\circ}\) і\(\angle c\).

    Кут\(70^{\circ}\) примикає до\(\angle c\) і два кути утворюють прямий кут.

    Далі виражаємо відносини за допомогою символів.

    \(\angle c+70^{\circ}=180^{\circ}\)

    Далі віднімаємо\(70^{\circ}\) з обох сторін рівняння.

    \(\angle c+70^{\circ}=180^{\circ}\)

    \(\angle c+70^{\circ}-70^{\circ}=180^{\circ} -70^{\circ}\)

    Потім спростіть обидві сторони рівняння.

    \(\angle c+70^{\circ}-70^{\circ}=180^{\circ} -70^{\circ}\)

    \(\angle c=110^{\circ}\)

    Відповідь є\(110^{\circ}\).

    \(m \angle c=110^{\circ}\)

    Приклад\(\PageIndex{1}\)

    Раніше вам дали проблему з приводу бейсбольного поля і фол ліній.

    Кут між траєкторією кулі і першою лінією фолу підстави потрібно з'ясувати. Це можна зробити за допомогою взаємодоповнюючих кутів.

    Рішення

    Спочатку намалюйте схему, щоб змоделювати проблему.

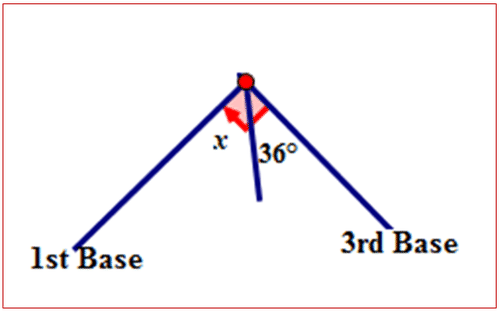    F-D_5982A7AE7106488EA77489ФБ75ДББ5БД ББ5 БДДС29287AF67AC67106BD20C+зображення_thumb_поштова листівка_крихітка_крихітка+зображення_thumb_поштова листівка_крихітка_Малюнок\(\PageIndex{8}\)

    Далі викласти відносини між\(36^{\circ}\) і\(\angle x\).

    \(36^{\circ}\)і\(\angle x\) є доповнюючими кутами. Сума кутів дорівнює\(90^{\circ}\).

    Далі виражаємо відносини за допомогою символів.

    \(36^{\circ}+\angle x=90^{\circ}\)

    Далі відніміть 36° з обох сторін рівняння.

    \(36^{\circ}+\angle x=90^{\circ}\)

    \(36^{\circ}-36^{\circ}+\angle x=90^{\circ}-36^{\circ}\)

    Потім спростіть обидві сторони рівняння.

    \(36^{\circ}-36^{\circ}+\angle x=90^{\circ}-36^{\circ}\)

    \(\angle x = 54^{\circ}\)

    Відповідь є\(54^{\circ}\).

    Кут\(54^{\circ}\) робиться між першою базовою лінією фолу і траєкторією бейсболу.

    Приклад\(\PageIndex{2}\)

    Якщо наступні кути взаємодоповнюють, знайдіть міру відсутнього кута.

    \(\angle A=37^{\circ}\)то\(\angle B=\)?

    Рішення

    Спочатку намалюйте схему, щоб змоделювати проблему.

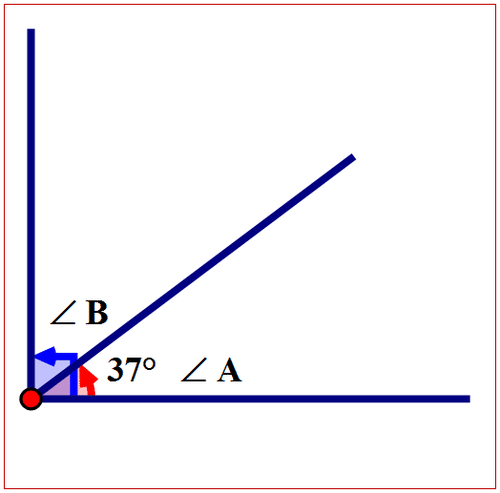    F-D_88C623F9C69a6535413F38655963D0b47af71e8EEEE4C6181C2B6+зображення_thumb_поштова листівка_крихітка+зображення_thumb_поштова листівка_крихітка_pngМалюнок\(\PageIndex{9}\)

    Далі викласти відносини між\(\angle A\) і\(\angle B\).

    \(\angle A\)і\(\angle B\) є доповнюючими кутами. Сума кутів дорівнює\(90^{\circ}\).

    Далі виражаємо відносини за допомогою символів.

    \(\angle A+ \angle B=90^{\circ}\)

    Далі підставляємо міру\(\angle A\) в рівняння.

    \(37^{\circ}+ \angle B=90^{\circ}\)

    Далі віднімаємо\(37^{\circ}\) з обох сторін рівняння.

    \(37^{\circ}+ \angle B=90^{\circ}\)

    \(37^{\circ}- 37^{\circ}+ \angle B=90^{\circ}- 37^{\circ}\)

    Потім спростіть обидві сторони рівняння.

    \(37^{\circ}- 37^{\circ}+ \angle B=90^{\circ}- 37^{\circ}\)

    \(\angle B =53^{\circ}\)

    Відповідь є\(53^{\circ}\).

    \(m \angle B =53^{\circ}\)

    Приклад\(\PageIndex{3}\)

    Якщо наступні кути є додатковими, знайдіть міру відсутнього кута.

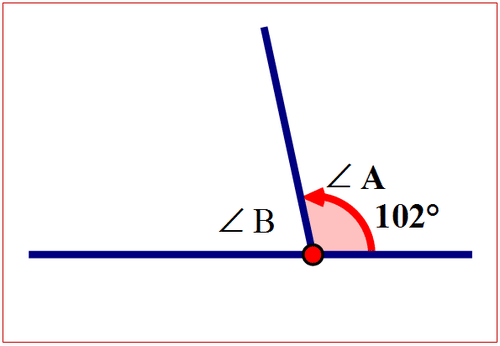
    \(\angle A=102^{\circ}\)то\(\angle B=\)?

    Рішення

    Спочатку намалюйте схему, щоб змоделювати проблему.

    F-D_E507515c762568877E2932DDD62BA617C194357A006ec627855b1FC+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_pngМалюнок\(\PageIndex{10}\)

    Далі викласти відносини між\(\angle A\) і\(\angle B\).

    \(\angle A\)і\(\angle B\) є додатковими кутами. Сума кутів становить 180°.

    Далі виражаємо відносини за допомогою символів.

    \(\angle A+ \angle B=180^{\circ}\)

    Далі підставляємо міру\(\angle A\) в рівняння.

    \(102^{\circ}+\angle B=180^{\circ}\)

    Далі віднімаємо\(102^{\circ}\) з обох сторін рівняння.

    \(102^{\circ}+\angle B=180^{\circ}\)

    \(102^{\circ}-102^{\circ}+\angle B=180^{\circ}-102^{\circ}\)

    Потім спростіть обидві сторони рівняння.

    \(102^{\circ}-102^{\circ}+\angle B=180^{\circ}-102^{\circ}\)

    \(\angle B=78^{\circ}\)

    Відповідь є\(78^{\circ}\).

    \(m \angle B=78^{\circ}\)

    Приклад\(\PageIndex{4}\)

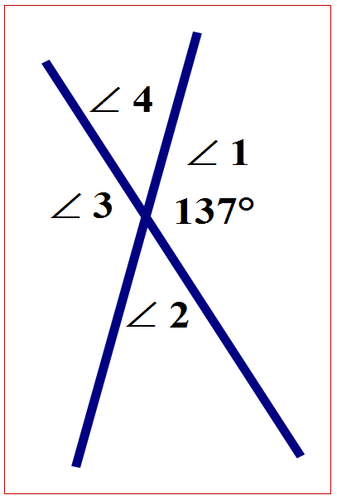
    Використовуючи наступну схему, визначте міри відсутніх кутів.

    F-D_C6046A248E9FDBA0E1AC835661C13D9E5720045231D4EFB8EDDE63+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_pngМалюнок\(\PageIndex{11}\)

    Рішення

    Спочатку сформулюйте взаємозв'язок між кутом\(\angle 1\) і\(\angle 3\).

    \(\angle 1\)і\(\angle 3\) є вертикальними кутами і рівні за мірою.

    Далі виражаємо відносини за допомогою символів.

    \(m\angle 1=m \angle 3\)

    Далі підставляємо міру\(\angle 1\) в рівняння.

    \(m\angle 1=m \angle 3\)

    \(137^{\circ}=m\angle 3\)

    Відповідь є\(137^{\circ}\).

    \(m\angle 3= 137^{\circ}\)

    Спочатку сформулюйте взаємозв'язок між кутом\(\angle 1\) і\(\angle 2\).

    \(\angle 1\)примикає до\(\angle 2\) і два кути утворюють прямий кут.

    Далі виражаємо відносини за допомогою символів.

    \(\angle 1+\angle 2=180^{\circ}\)

    Далі підставляємо міру\(\angle 1\) в рівняння.

    \(137^{\circ}+\angle 2=180^{\circ}\)

    Далі віднімаємо\(137^{\circ}\) з обох сторін рівняння.

    \(137^{\circ}+\angle 2=180^{\circ}\)

    \(137^{\circ}-137^{\circ}+\angle 2=180^{\circ}-137^{\circ}\)

    Потім спростіть обидві сторони рівняння.

    \(137^{\circ}-137^{\circ}+\angle 2=180^{\circ}-137^{\circ}\)

    \(\angle 2=43^{\circ}\)

    Відповідь є\(43^{\circ}\).

    \(m \angle 2=43^{\circ}\)

    Спочатку сформулюйте взаємозв'язок між кутом\(\angle 2\) і\(\angle 4\).

    \(\angle 2\)і\(\angle 4\) є вертикальними кутами і рівні за мірою.

    Далі виражаємо відносини за допомогою символів.

    \(m \angle 2=m \angle 4\)

    Далі підставляємо міру\(\angle 2\) в рівняння.

    \(m \angle 2=m \angle 4\)

    \(43^{\circ}=m \angle 4\)

    Відповідь є\(43^{\circ}\).

    \(m \angle 4=43^{\circ}\)

    Рецензія

    Якщо наступні кутові пари взаємодоповнюють, то яка міра відсутнього кута?

    1. Якщо\(\angle A=45^{\circ}\) тоді\(\angle B=\)?

    2. Якщо\(\angle C=83^{\circ}\) тоді\(\angle D=\)?

    3. Якщо\(\angle E=33^{\circ}\) тоді\(\angle F=\)?

    4. Якщо\(\angle G=53^{\circ}\) тоді\(\angle H=\)?

    Якщо наступні пари кутів є додатковими, то яка міра відсутнього кута?

    5. Якщо\(\angle A=40^{\circ}\) тоді\(\angle B=\)?

    6. Якщо\(\angle A=75^{\circ}\) тоді\(\angle B=\)?

    7. Якщо\(\angle C=110^{\circ}\) тоді\(\angle F=\)?

    8. Якщо\(\angle D=125^{\circ}\) тоді\(\angle E=\)?

    9. Якщо\(\angle M=10^{\circ}\) тоді\(\angle N=\)?

    10. Якщо\(\angle O=157^{\circ}\) тоді\(\angle P=\)?

    Визначте наступні типи кутових пар.

    11. Вертикальні кути

    12. Сусідні кути

    13. Додаткові кути

    14. Додаткові кути

    15. Внутрішні кути

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 6.4.

    Ресурси

    Лексика

    Термін Визначення
    Сусідні кути Два кути є суміжними, якщо вони поділяють сторону і вершину. Слово «суміжний» означає «поруч» або «поруч з».
    Кут Геометрична фігура, утворена двома променями, які з'єднуються в одній точці або вершині.
    Лінії, що перетинаються Пересічні лінії - це лінії, які перетинаються або зустрічаються в якійсь точці.
    Паралельний Дві або більше ліній паралельні, коли вони лежать в одній площині і ніколи не перетинаються. Ці лінії завжди будуть мати однаковий ухил.
    перпендикулярні лінії Перпендикулярні лінії - це лінії, які перетинаються під\(90^{\circ}\) кутом.
    Прямий кут Прямим кутом є пряма, рівна\(180^{\circ}\).

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Додаткові, Додаткові та Вертикальні кути

    Практика: Кутові властивості та теореми